Содержание
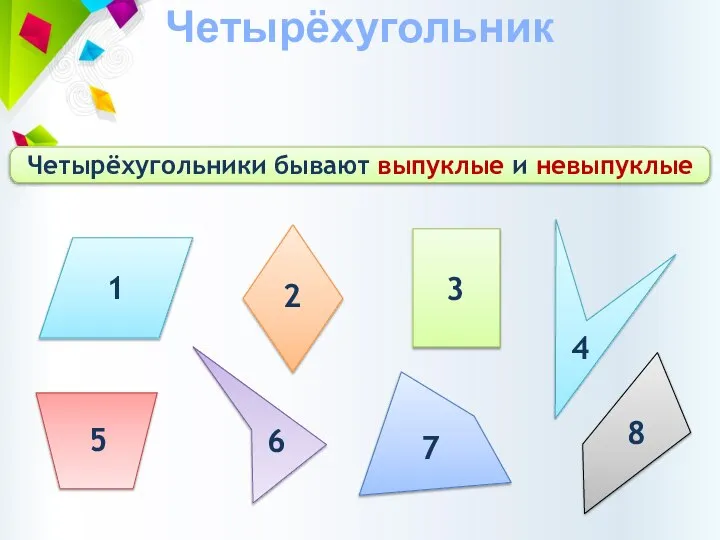
- 2. Четырёхугольник Четырёхугольники бывают выпуклые и невыпуклые
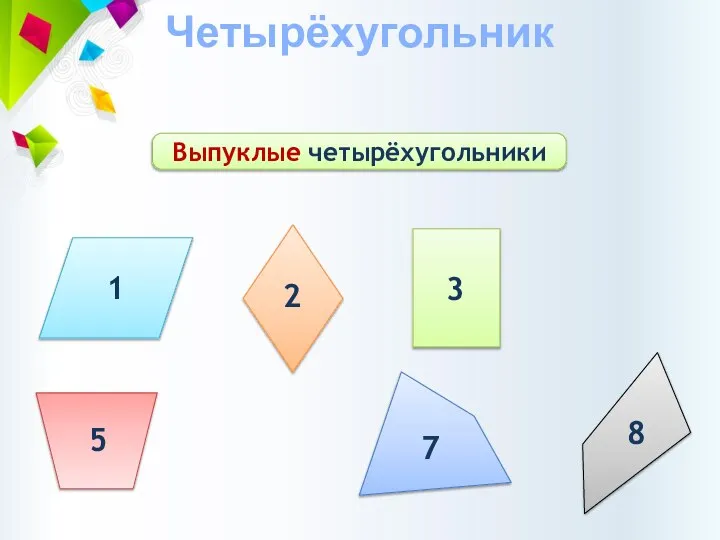
- 3. Четырёхугольник Выпуклые четырёхугольники
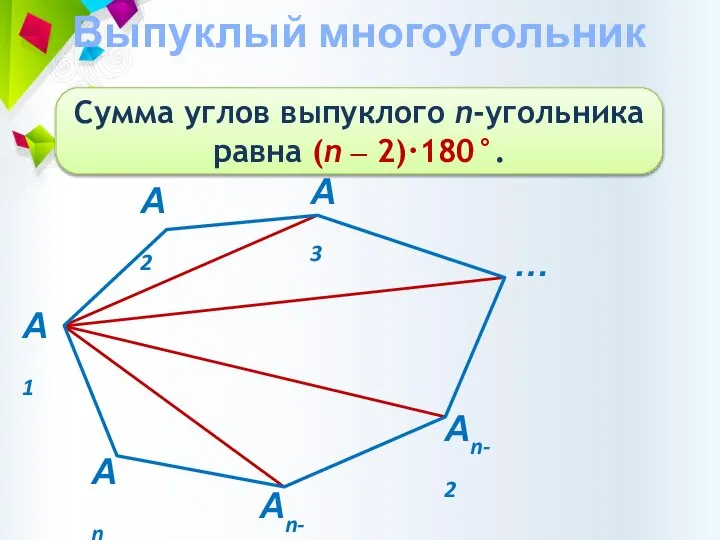
- 4. Выпуклый многоугольник Сумма углов выпуклого n-угольника равна (n ‒ 2)·180°.
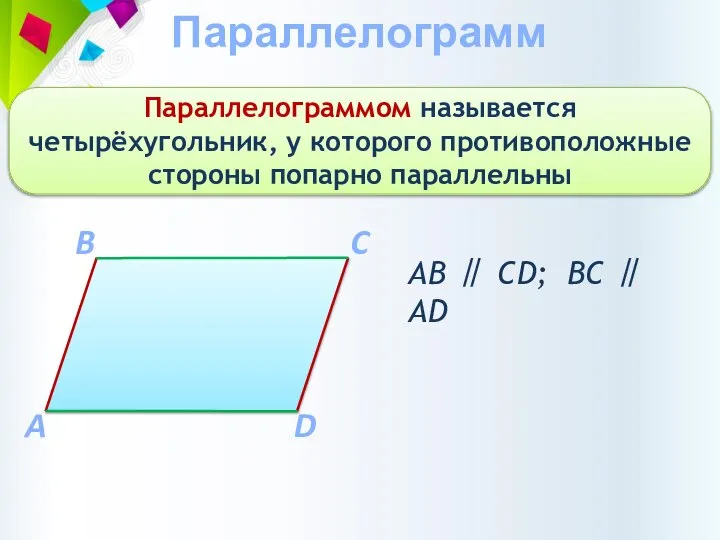
- 5. Параллелограмм Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны A C B D АВ ∥
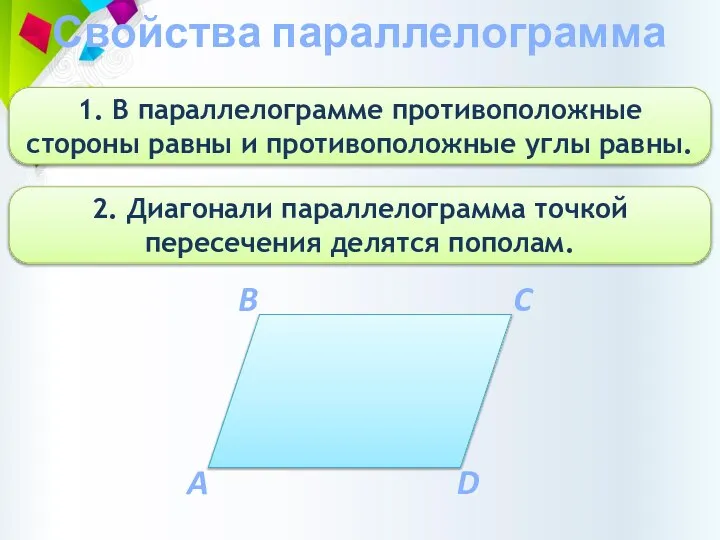
- 6. Свойства параллелограмма 1. В параллелограмме противоположные стороны равны и противоположные углы равны. 2. Диагонали параллелограмма точкой
- 7. Признаки параллелограмма 1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник ‒ параллелограмм.
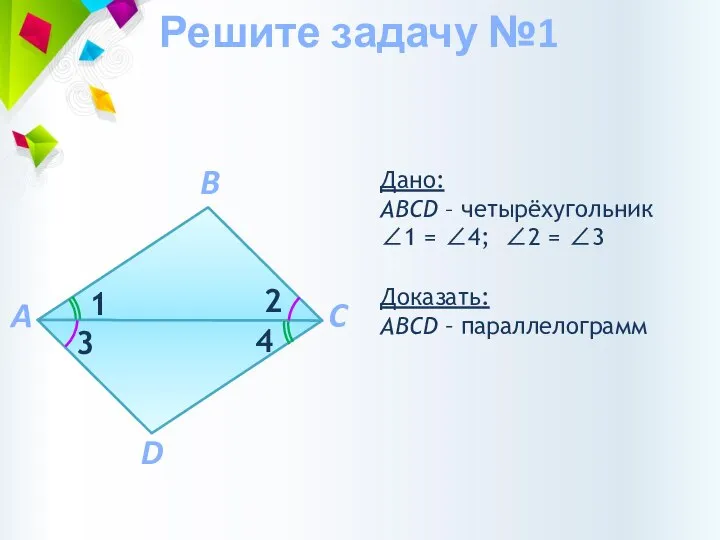
- 8. Доказать: АВCD – параллелограмм Дано: АВCD – четырёхугольник ∠1 = ∠4; ∠2 = ∠3 Решите задачу
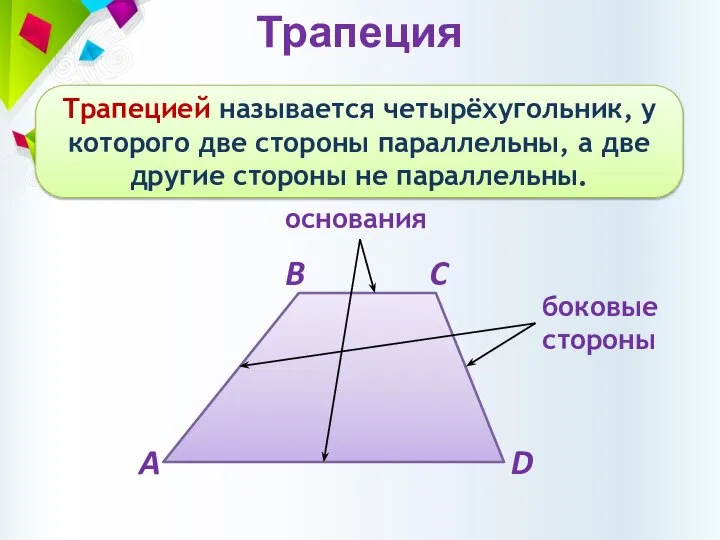
- 9. Трапеция Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. основания
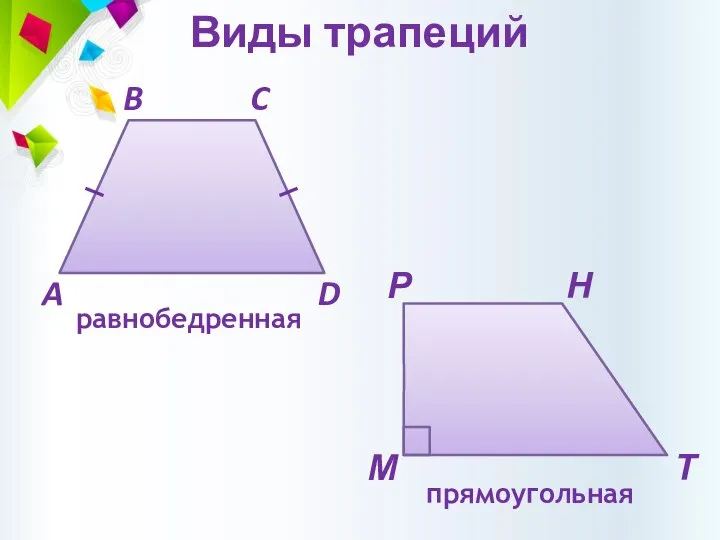
- 10. Виды трапеций прямоугольная равнобедренная
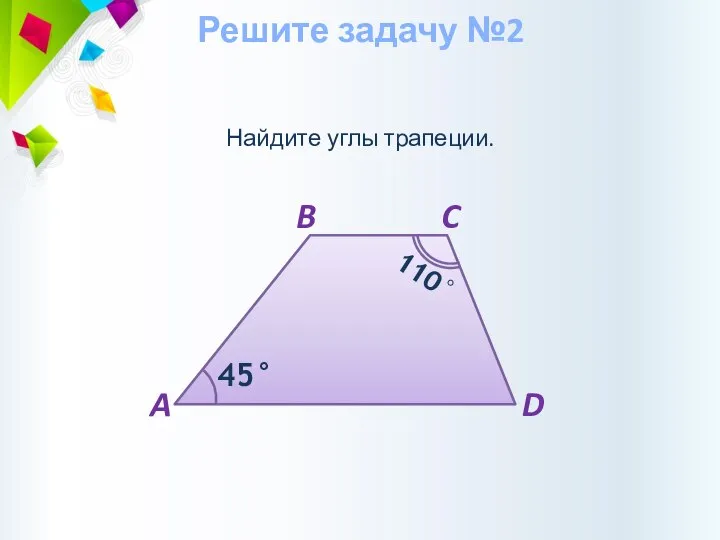
- 11. Найдите углы трапеции. Решите задачу №2
- 12. Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые A C B D ∠А=∠В=∠С=∠D=90° АВ ∥
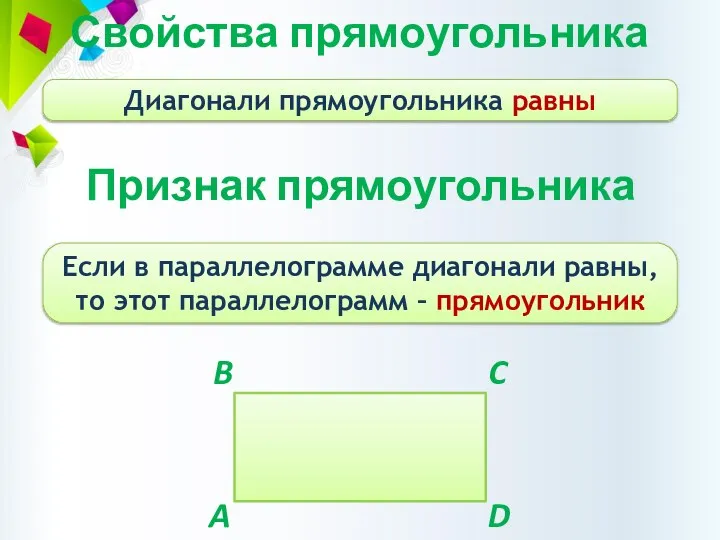
- 13. Свойства прямоугольника Диагонали прямоугольника равны Признак прямоугольника Если в параллелограмме диагонали равны, то этот параллелограмм –
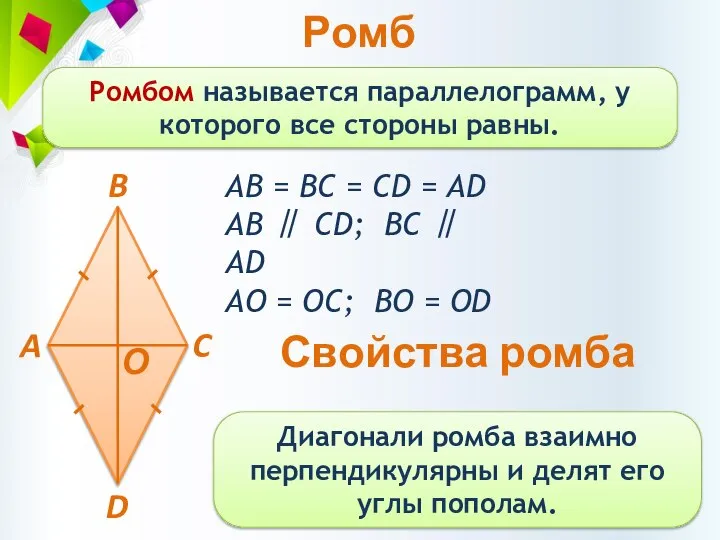
- 14. Ромб Ромбом называется параллелограмм, у которого все стороны равны. АВ = BC = CD = AD
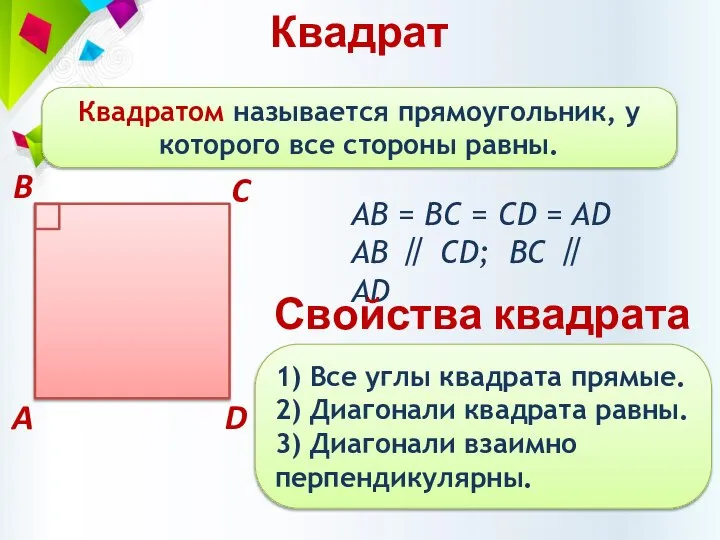
- 15. Квадрат Квадратом называется прямоугольник, у которого все стороны равны. АВ = BC = CD = AD
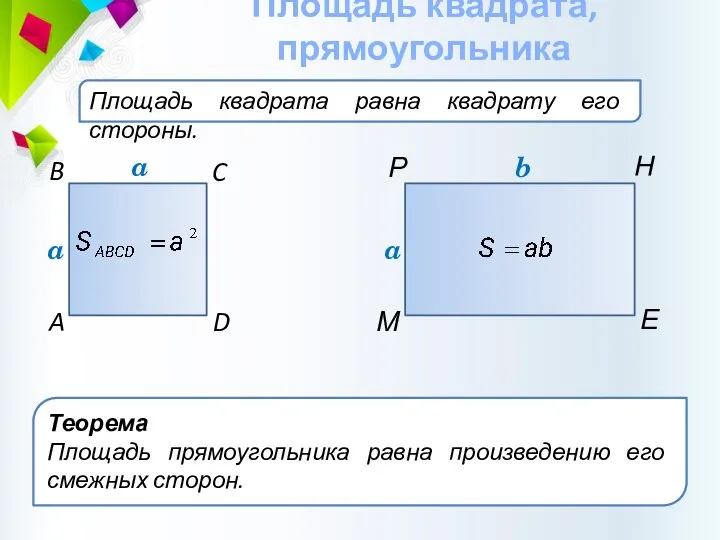
- 16. Площадь квадрата равна квадрату его стороны. Площадь квадрата, прямоугольника C B D A a Теорема Площадь
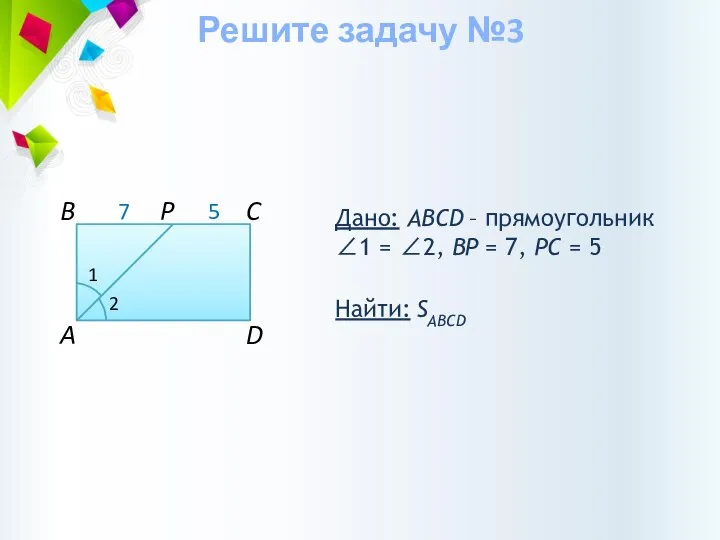
- 17. Дано: ABCD – прямоугольник ∠1 = ∠2, BP = 7, РC = 5 Найти: SABCD P
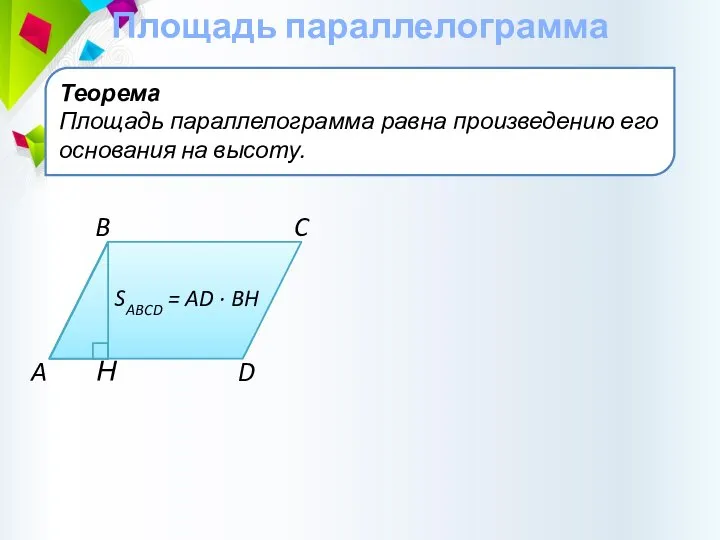
- 18. Теорема Площадь параллелограмма равна произведению его основания на высоту. Площадь параллелограмма C B D A Н
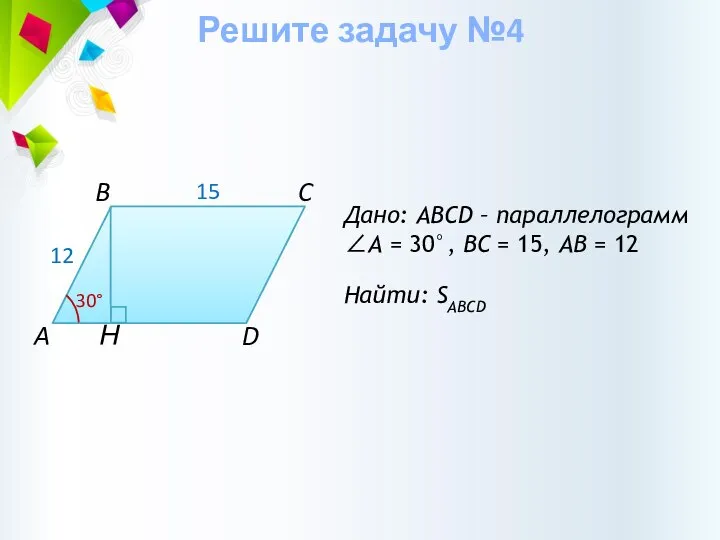
- 19. Н Дано: ABCD – параллелограмм ∠А = 30°, BС = 15, АВ = 12 Найти: SABCD
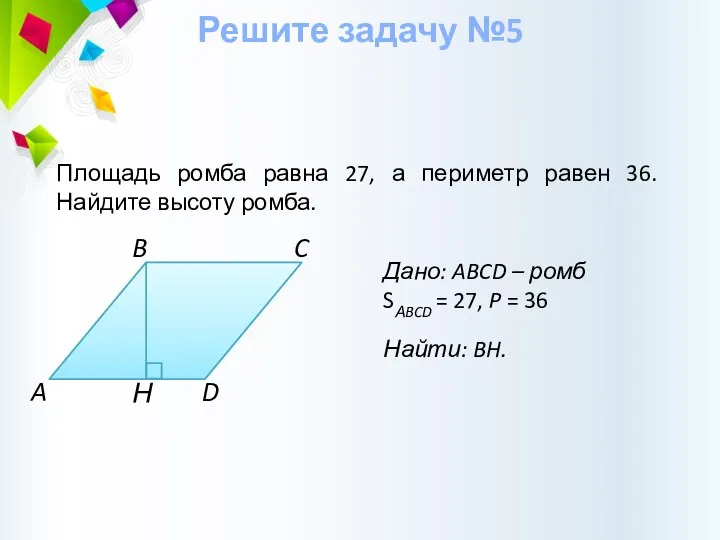
- 20. Н Дано: ABCD – ромб SАBCD = 27, P = 36 Найти: BH. Решите задачу №5
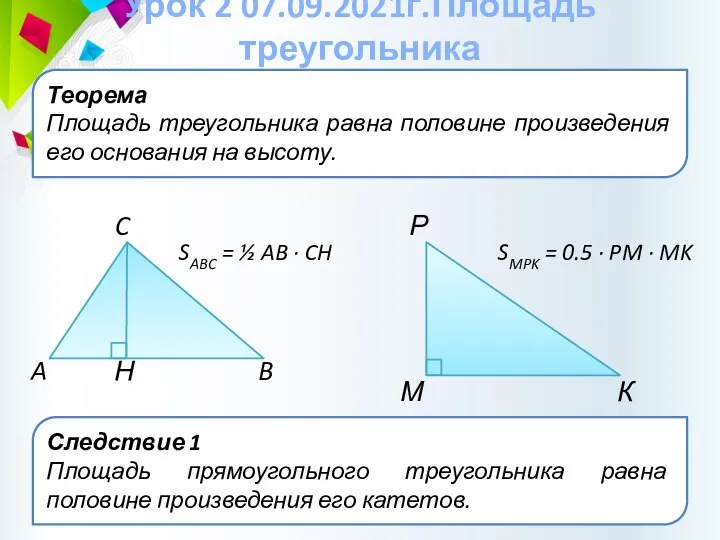
- 21. Теорема Площадь треугольника равна половине произведения его основания на высоту. Урок 2 07.09.2021г.Площадь треугольника C B
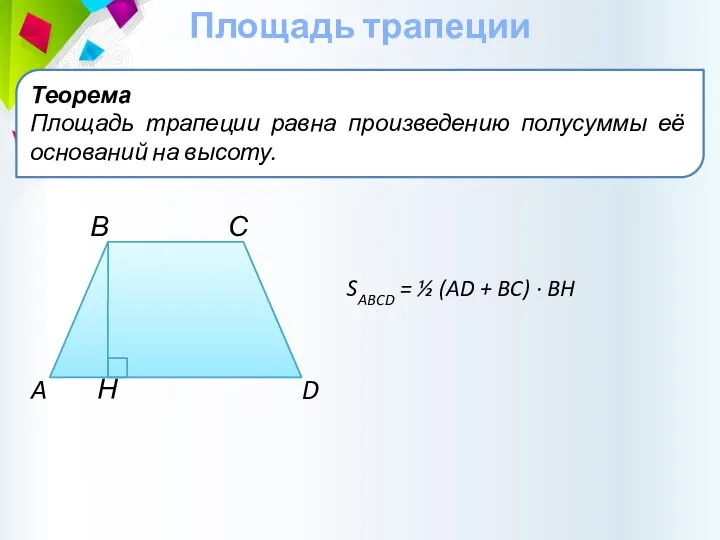
- 22. Площадь трапеции Теорема Площадь трапеции равна произведению полусуммы её оснований на высоту. В С A Н
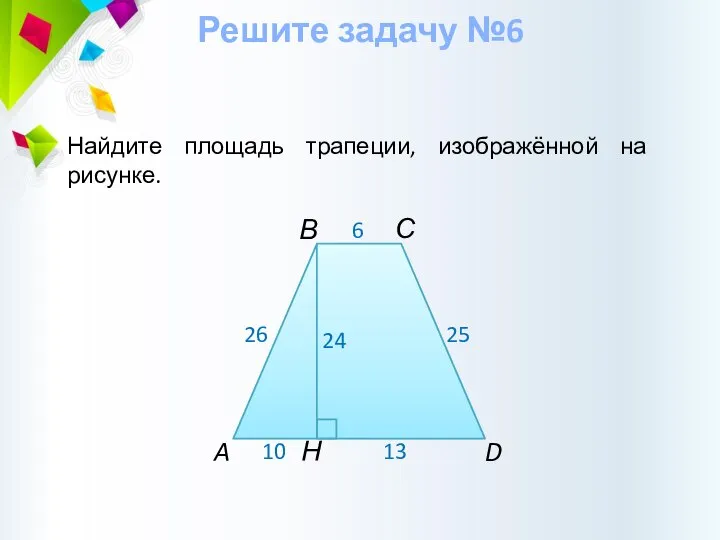
- 23. Решите задачу №6 Найдите площадь трапеции, изображённой на рисунке.
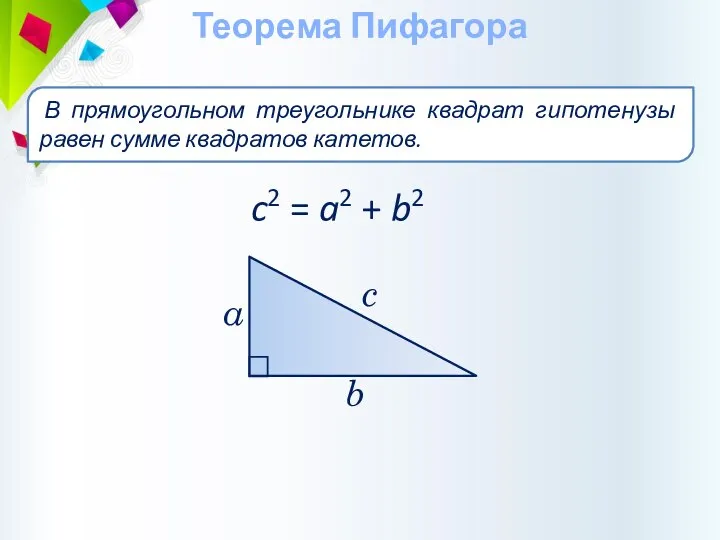
- 24. Теорема Пифагора c2 = a2 + b2 c b В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 25. Первый признак подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого, то такие
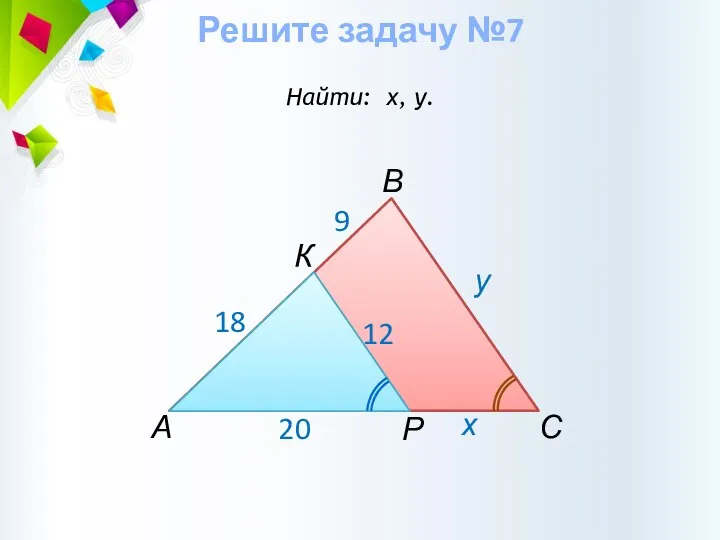
- 26. Решите задачу №7 Найти: х, у. А В С у х Р К 18 20 9
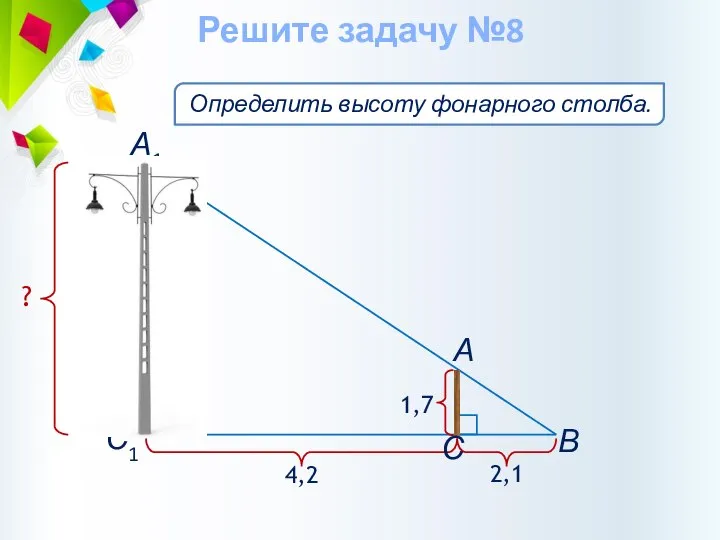
- 27. Определить высоту фонарного столба. Решите задачу №8
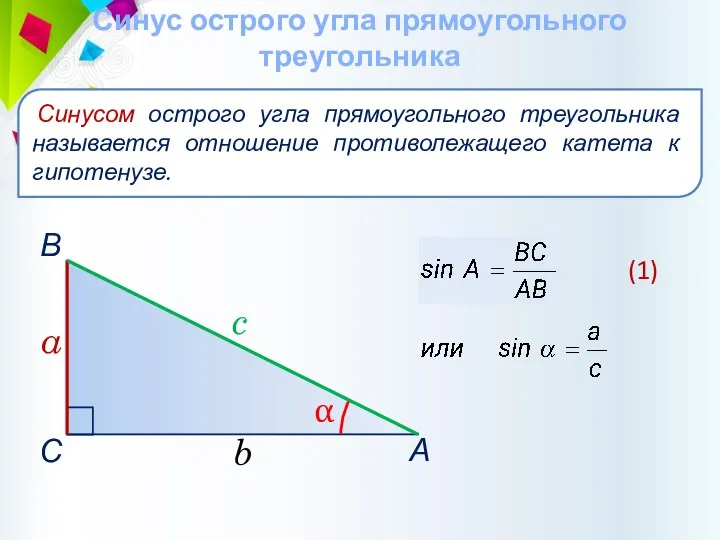
- 28. Синус острого угла прямоугольного треугольника Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
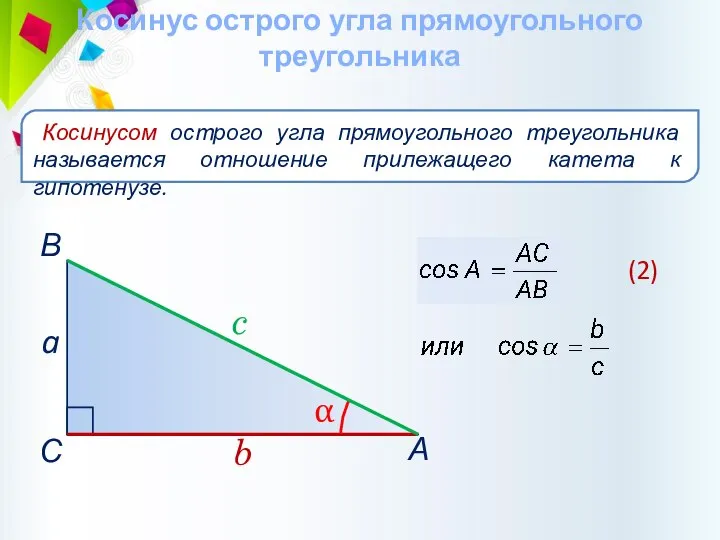
- 29. Косинус острого угла прямоугольного треугольника Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
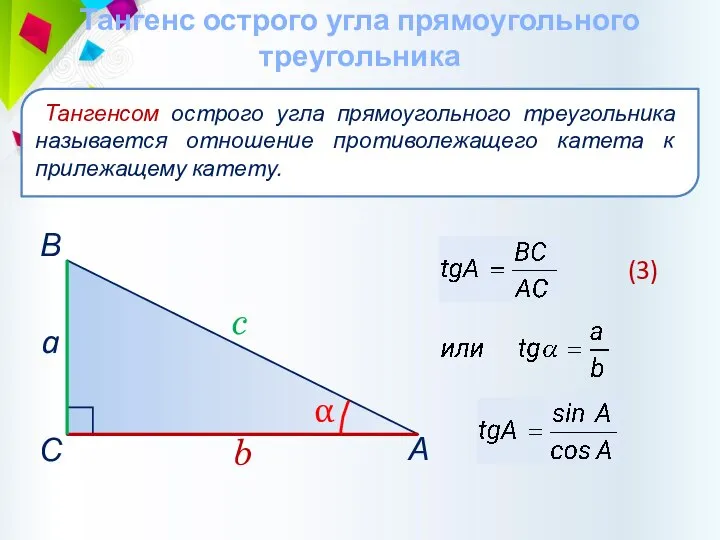
- 30. Тангенс острого угла прямоугольного треугольника Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
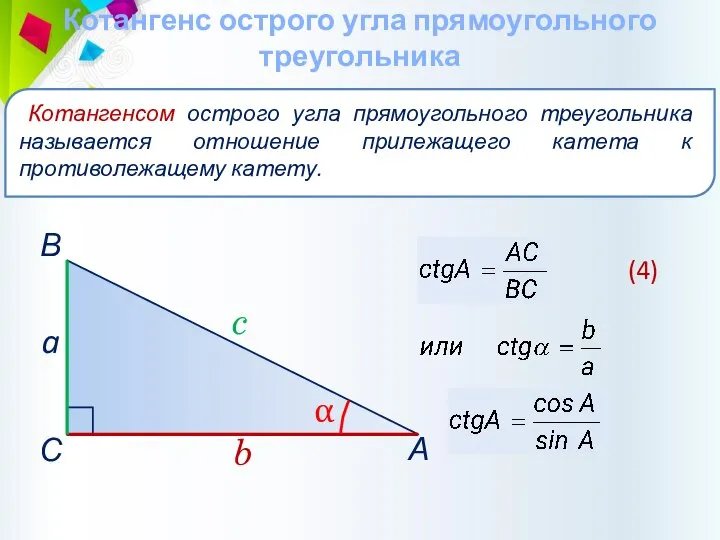
- 31. Котангенс острого угла прямоугольного треугольника Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему
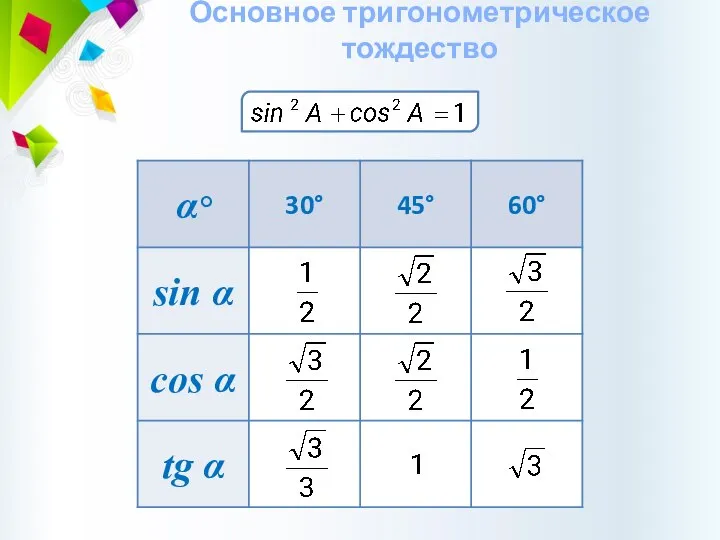
- 32. Основное тригонометрическое тождество
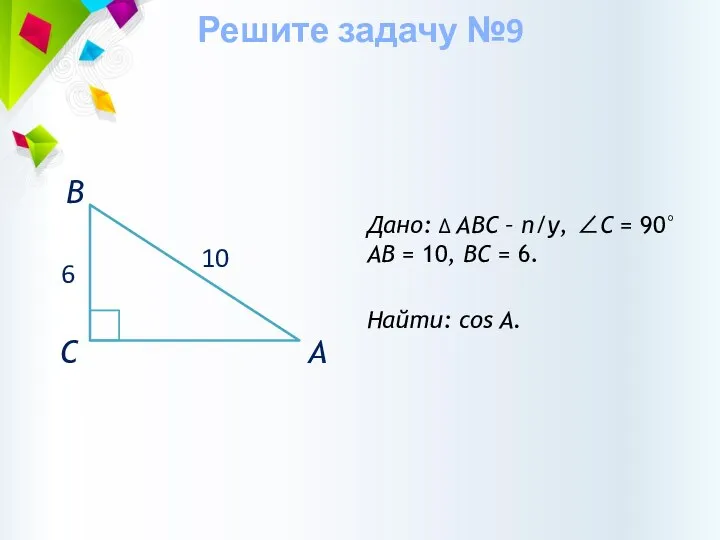
- 33. Дано: ∆ АВС – п/у, ∠С = 90° АВ = 10, ВС = 6. Найти: cos
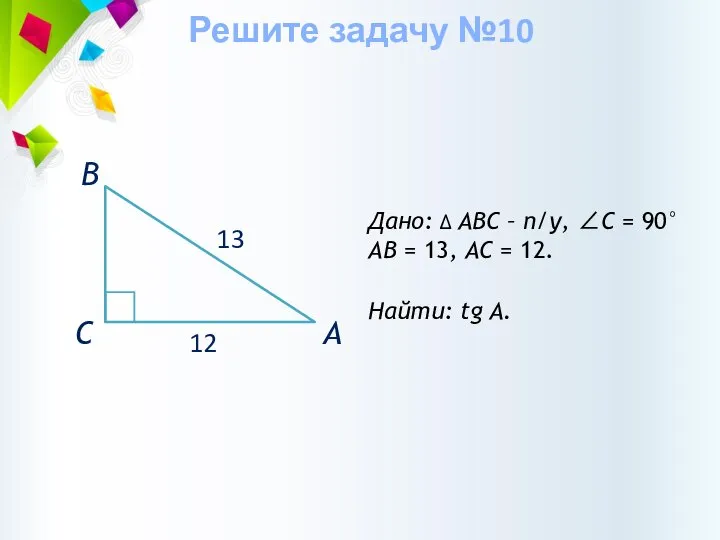
- 34. Дано: ∆ АВС – п/у, ∠С = 90° АВ = 13, АС = 12. Найти: tg
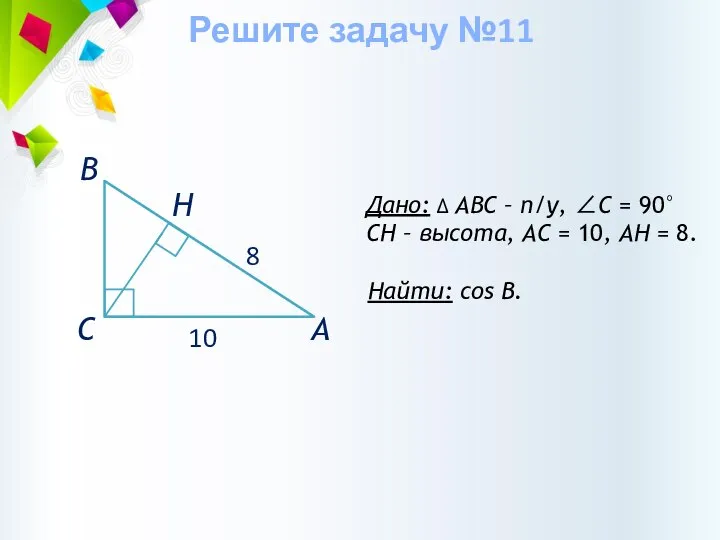
- 35. Дано: ∆ АВС – п/у, ∠С = 90° CH – высота, АС = 10, АН =
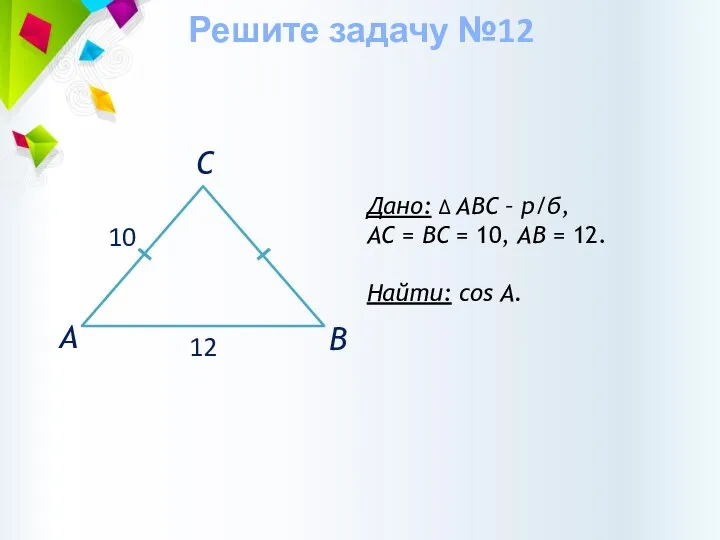
- 36. Дано: ∆ АВС – р/б, АС = ВС = 10, АВ = 12. Найти: cos А.
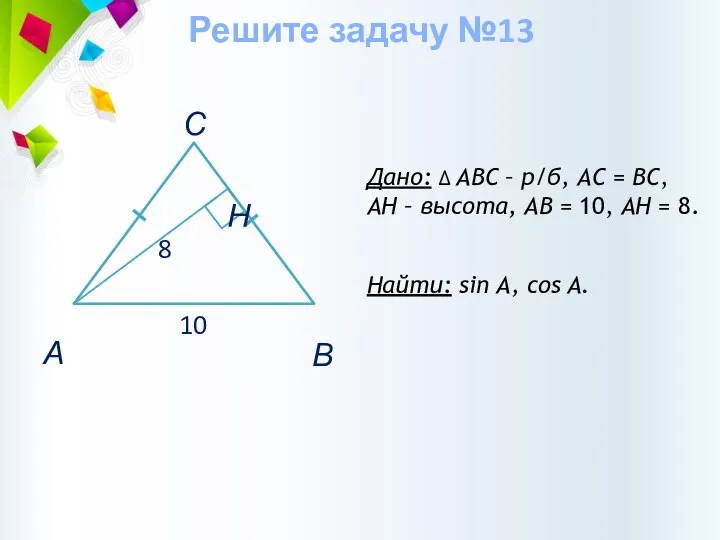
- 37. Дано: ∆ АВС – р/б, АС = ВС, AH – высота, АВ = 10, AH =
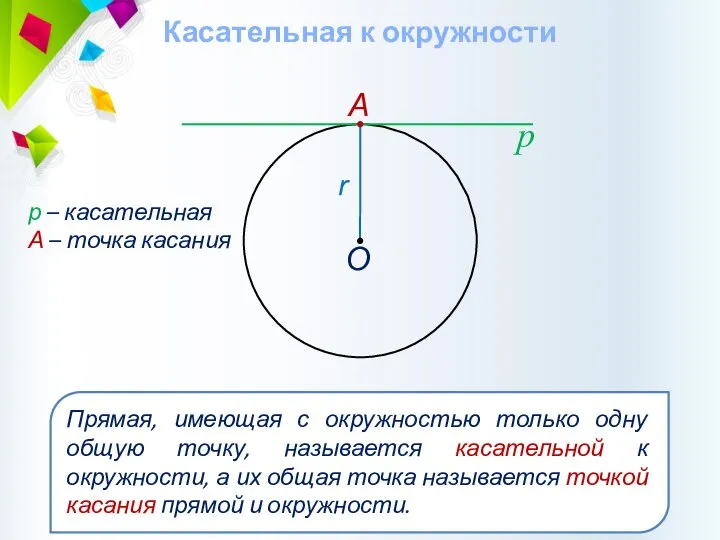
- 38. Касательная к окружности р р – касательная А – точка касания А О Прямая, имеющая с
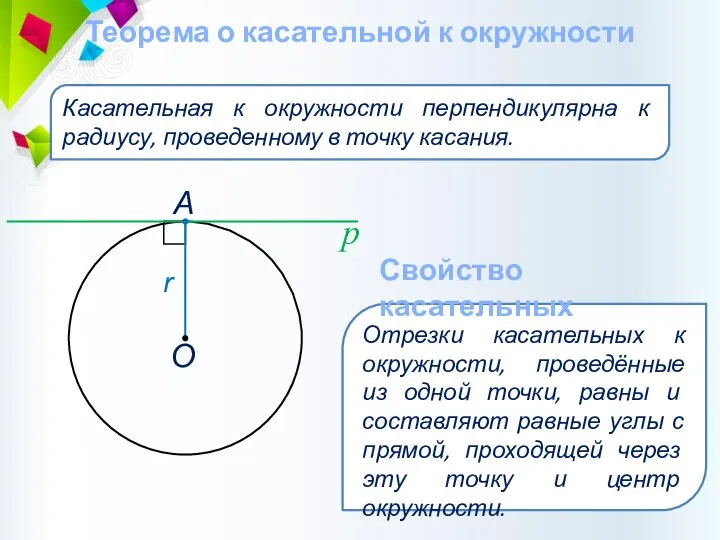
- 39. Теорема о касательной к окружности Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Отрезки
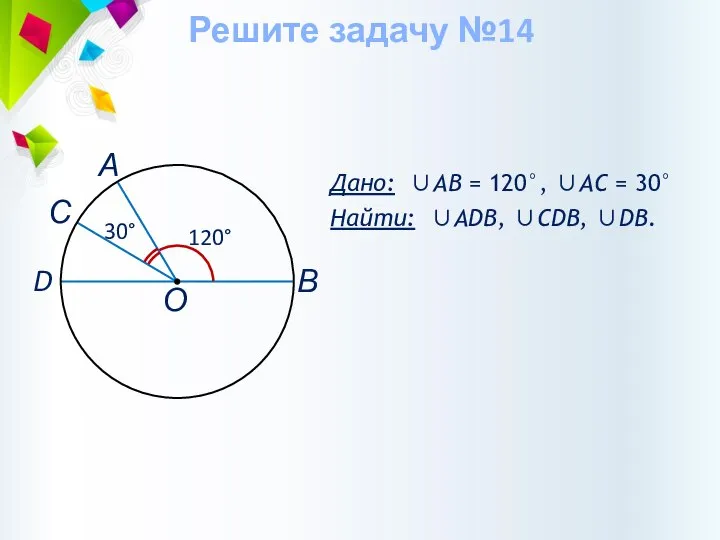
- 40. Дано: ∪АВ = 120°, ∪AC = 30° Найти: ∪АDВ, ∪CDB, ∪DB. Решите задачу №14
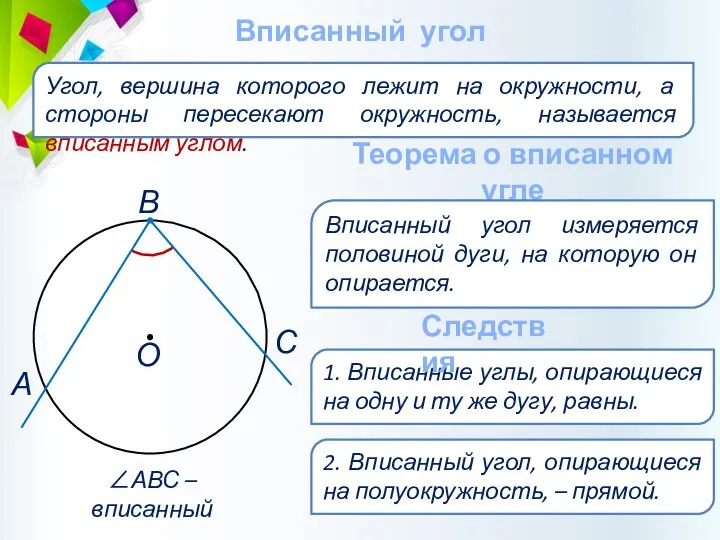
- 41. Вписанный угол Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. ∠АВС
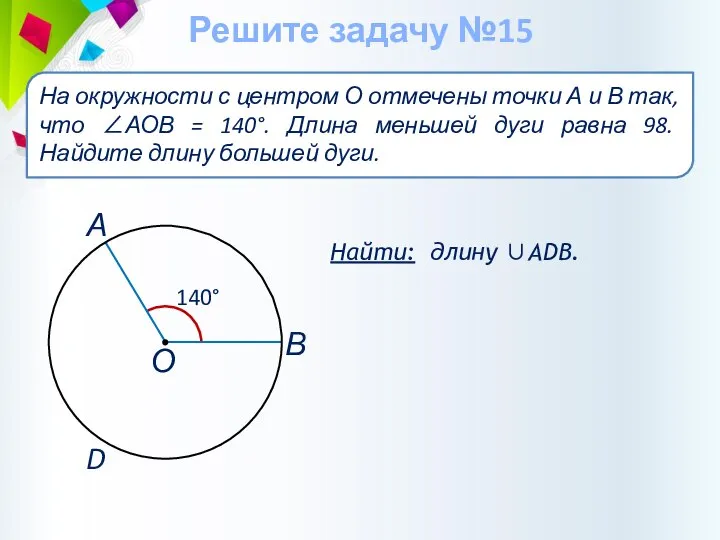
- 42. Найти: длину ∪АDВ. На окружности с центром О отмечены точки А и В так, что ∠АОВ
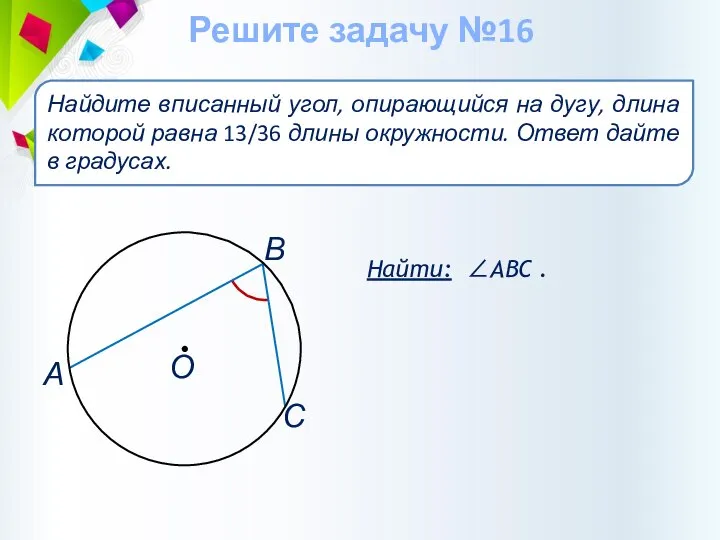
- 43. Найти: ∠АВС . Найдите вписанный угол, опирающийся на дугу, длина которой равна 13/36 длины окружности. Ответ
- 45. Скачать презентацию



 Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Основы системной динамики
Основы системной динамики Логарифмические уравнения. Уравнения, решаемые методом введения новой переменной
Логарифмические уравнения. Уравнения, решаемые методом введения новой переменной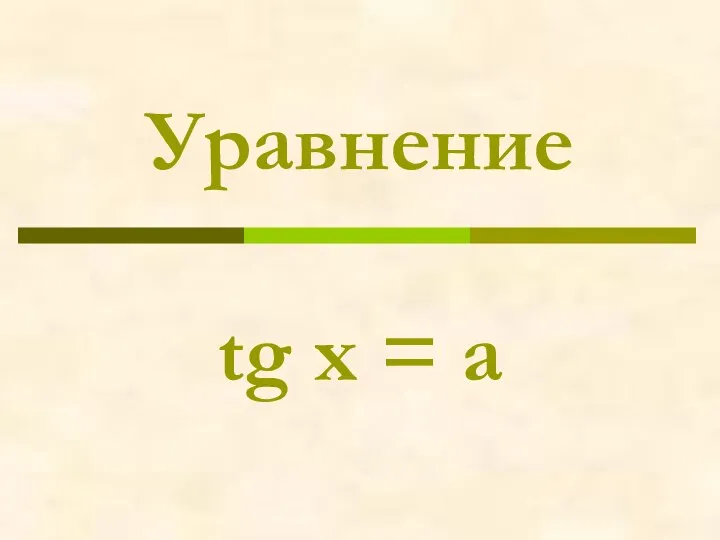 Уравнение tg x = a
Уравнение tg x = a Презентация на тему Смежные и вертикальные углы
Презентация на тему Смежные и вертикальные углы  Роль семьи в развитии речи ребенка
Роль семьи в развитии речи ребенка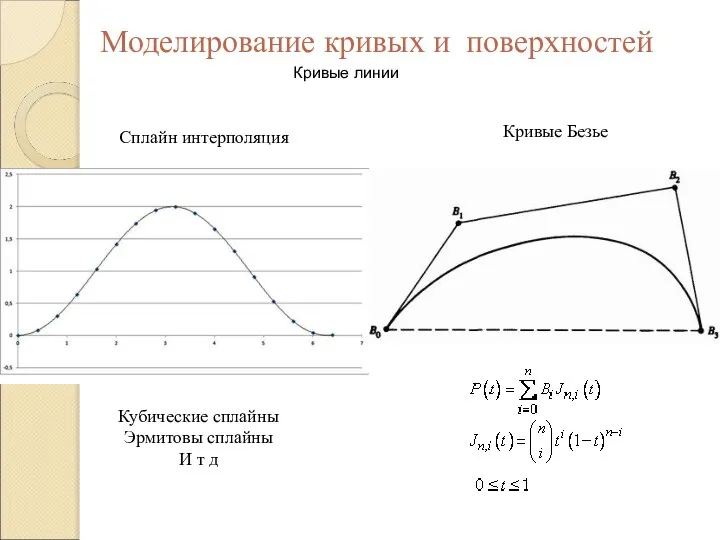 Моделирование кривых и поверхностей
Моделирование кривых и поверхностей Геометрический смысл производной. Решение примеров на геометрический смысл производной
Геометрический смысл производной. Решение примеров на геометрический смысл производной Объем конуса
Объем конуса Математическое моделирование. Основные положения
Математическое моделирование. Основные положения Математическое моделирование
Математическое моделирование Решение задач
Решение задач Числовые ряды, основные определения и свойства
Числовые ряды, основные определения и свойства Проверочная работа по теме Кровь
Проверочная работа по теме Кровь Свойства тригонометрических функций
Свойства тригонометрических функций УРОК МАТЕМАТИКИ В 5 кл. Учитель: Батычёк Т.Н.
УРОК МАТЕМАТИКИ В 5 кл. Учитель: Батычёк Т.Н. Математическое и программное обеспечение многопользовательских тренажеров с погружением в иммерсивные виртуальные среды
Математическое и программное обеспечение многопользовательских тренажеров с погружением в иммерсивные виртуальные среды Урок – творческий проект по математике Мастерская игрушек
Урок – творческий проект по математике Мастерская игрушек Золотое сечение и гармония форм природы и искусства. 8 класс
Золотое сечение и гармония форм природы и искусства. 8 класс Старинные меры веса 1 класс - Презентация по математике_
Старинные меры веса 1 класс - Презентация по математике_ Теплицы
Теплицы Пропорциональные отрезки в прямоугольном треугольнике (8 класс)
Пропорциональные отрезки в прямоугольном треугольнике (8 класс) Засели числовые домики
Засели числовые домики Уравнения с одной переменной
Уравнения с одной переменной Математичний диктант. Паралелограм
Математичний диктант. Паралелограм Увеличение и уменьшение в одно и то же число раз
Увеличение и уменьшение в одно и то же число раз النشاط الثالث
النشاط الثالث О математическом языке
О математическом языке