Содержание
- 2. Устная работа 1. Дайте определение арифметической прогрессии. 2. Что называется разностью арифметической прогрессии? 3. Запишите формулу
- 3. Диктант 1. В арифметической прогрессии первый член равен 8, второй 4. Чему равна разность этой прогрессии?
- 4. Диктант 5. Найдите сумму нечётных чисел от 1 до 23 включительно. 4. Найдите разность арифметической прогрессии,
- 5. Диктант 5. Найдите сумму нечётных чисел от 1 до 23 включительно. 4. Найдите разность арифметической прогрессии,
- 6. Ответы: 1. d = - 4 6. 1) 24 2) 8 3) 54 2. а3 =
- 8. Формула n-го члена прогрессии Пусть заданы а1 и d а2=а1+d a3=a2+d=a1+d+d=а1+2d a4=a3+d=а1+3d …………………………….. an=a1+(n-1)d Пусть заданы
- 9. Определение Арифметической Геометрической прогрессией а1,а2,а3,…аn,.. b1,b2,b3,…bn,… называется последовательность, отличных от нуля чисел каждый член которой, начиная
- 10. Определение Числовая последовательность а1,а2,а3,…аn,.. b1,b2,b3,…bn,… называется арифметической геометрической если для всех натуральных n выполняется равенство an+1=
- 11. Вывод d>0 арифметическая прогрессия возрастающая d арифметическая прогрессия убывающая q > 1 геометрическая прогрессия возрастающая 0
- 12. Формула n-го члена прогрессии Пусть заданы а1 и d а2=а1+d a3=a2+d=a1+d+d=а1+2d a4=a3+d=а1+3d …………………………….. an=a1+(n-1)d Пусть заданы
- 13. Определите вид прогрессии В третьем тысячелетии високосными годами будут 2008, 2012 ,2016, 2020. В какой последовательности
- 14. Составьте геометрическую прогрессию: Ежедневно каждый болеющий гриппом может заразить четырех окружающих. 1; 4; 16; 64;… Дима
- 15. Работа в тетрадях Задание 1. Дано: (bn ) - геометрическая прогрессия b1= 5 q = 3
- 16. Работа в тетрадях Задание 2. Дано: (bn ) - геометрическая прогрессия b4= 40 q = 2
- 17. Работа в тетрадях Задание 3. Дано: (bn ) - геометрическая прогрессия b1= -2, b4=-54. Найти: q.
- 18. Математике должно учить в школе ещё с той целью, чтобы познания, здесь приобретаемые были достаточными для
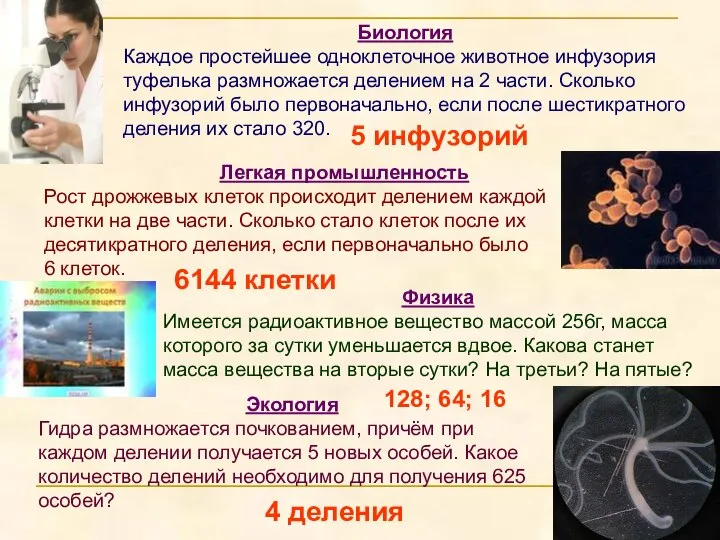
- 19. Биология Каждое простейшее одноклеточное животное инфузория туфелька размножается делением на 2 части. Сколько инфузорий было первоначально,
- 20. Подготовка к ГИА Заданы три первых члена числовых последовательностей. Известно, что одна из этих последовательностей не
- 21. Подготовка к ГИА Заданы три первых члена числовых последовательностей. Известно, что одна из этих последовательностей не
- 22. Подготовка к ГИА Последовательности (an), (bn), (cn) заданы формулами n-го члена. Поставьте в соответствие каждой последовательности
- 23. Домашнее задание Придумайте или найдите задачи, позволяющие использовать геометрическую прогрессию; оформите их решение в тетрадь.
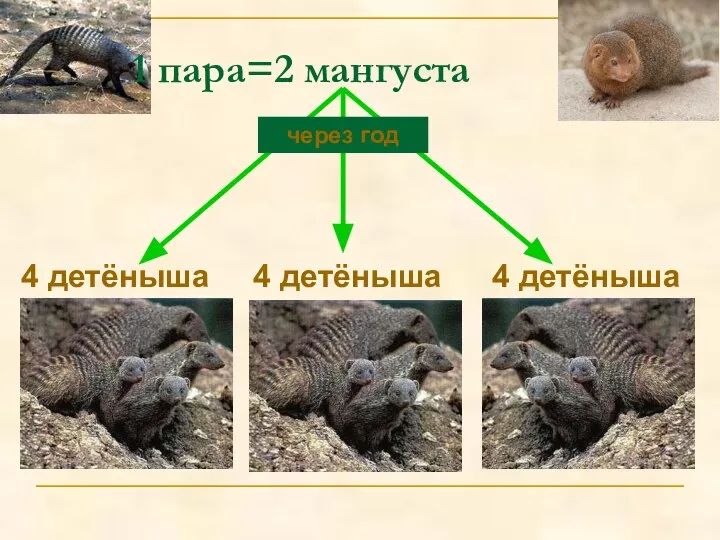
- 24. МАНГУСТ Мангуст – пушистый зверёк, родина которого – Индия. Длина тела ~ 50-60см. Даёт потомство 3
- 25. 4 детёныша 4 детёныша 4 детёныша через год 1 пара=2 мангуста
- 26. Сколько будет детёнышей, если образовалось 6 пар и каждая пара даёт 12 детёнышей? 1–й год –
- 27. Сколько детёнышей мангустов появится на 10-й год? в10 = 20 155 392 детёныша
- 29. Скачать презентацию
























 Формула у=х2
Формула у=х2 Сложение двух векторов
Сложение двух векторов Перпендикулярность в пространстве. Тест. Практическая часть
Перпендикулярность в пространстве. Тест. Практическая часть Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Десятичные дроби
Десятичные дроби Путешествие в страну Геометрию
Путешествие в страну Геометрию Площади многоугольников. Решение прикладных задач
Площади многоугольников. Решение прикладных задач Площадь круга
Площадь круга Цилиндр. 4 класс
Цилиндр. 4 класс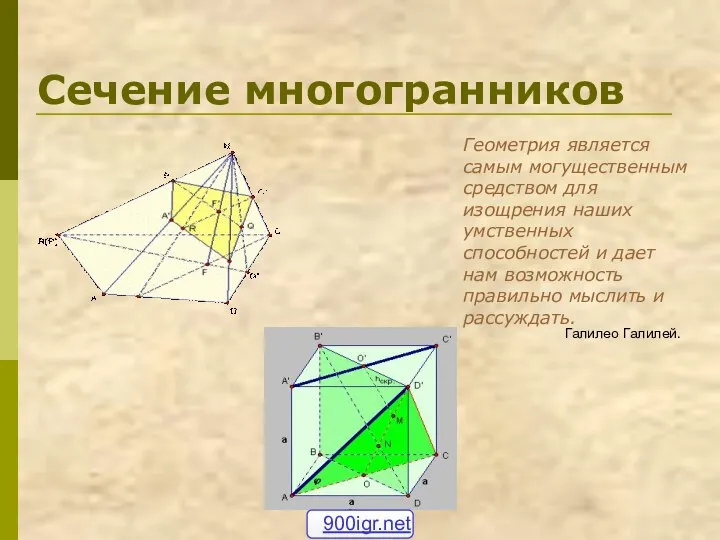 Сечение многогранника плоскостью
Сечение многогранника плоскостью Калькуляционная карточка. Тесто заварное
Калькуляционная карточка. Тесто заварное Презентация на тему Вычитание
Презентация на тему Вычитание  Построение сечений в тетраэдре
Построение сечений в тетраэдре Деление с остатком. 4 класс
Деление с остатком. 4 класс Признаки подобия треугольников (урок-практикум)
Признаки подобия треугольников (урок-практикум) Равенство геометрических фигур
Равенство геометрических фигур Исследуйте выражения
Исследуйте выражения Явная разностная схема для полной системы уравнений Навье-Стокса
Явная разностная схема для полной системы уравнений Навье-Стокса Презентация на тему Второй признак равенства треугольников 7 класс
Презентация на тему Второй признак равенства треугольников 7 класс  5b6b504ca82342859c8bde10a1b9f03b
5b6b504ca82342859c8bde10a1b9f03b Демо версия. Математика 2.3
Демо версия. Математика 2.3 Дорогу осилит идущий, геометрию – думающий. Площадь параллелограмма
Дорогу осилит идущий, геометрию – думающий. Площадь параллелограмма Геометрическое шоу Десять пятерок
Геометрическое шоу Десять пятерок Простейшие преобразования графиков
Простейшие преобразования графиков Линейные уравнения и системы уравнений. Повторение
Линейные уравнения и системы уравнений. Повторение Межлабораторные сравнительные испытания и сличения
Межлабораторные сравнительные испытания и сличения Решение систем уравнений методом итерации функции. 10 класс
Решение систем уравнений методом итерации функции. 10 класс