Аксиомы стереометрии

(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без доказательства
Аксиома.

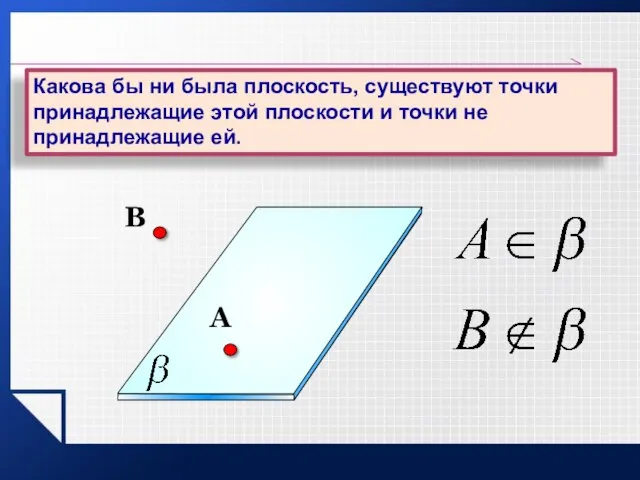
A
B
Какова бы ни была плоскость, существуют точки принадлежащие этой плоскости и точки не принадлежащие ей.

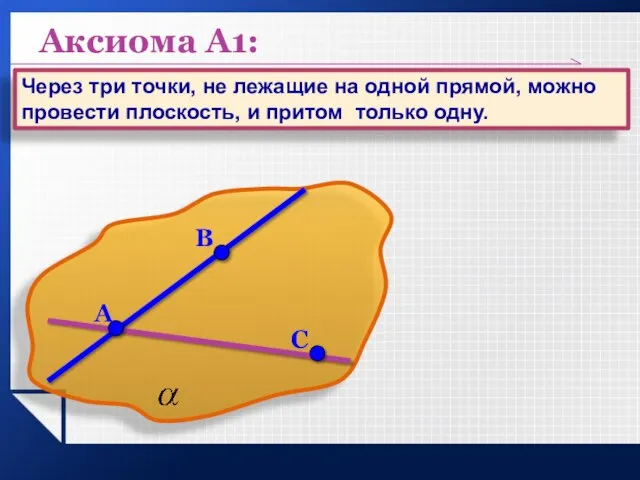
Аксиома А1:
Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Иллюстрации к теореме из жизни.
Табурет с тремя ножками всегда идеально встанет на пол и не будет качаться. У табурета с четырьмя ножками бывают проблемы с устойчивостью, если ножки стула не одинаковые по длине. Табурет качается, т. е. опирается на три ножки, а четвертая ножка (четвертая «точка») не лежит в плоскости пола, а висит в воздухе.
Для видеокамеры, фотосъемки и для других приборов часто используют штатив – треногу. Три ножки штатива устойчиво расположатся на любом полу в помещениях, на асфальте или прямо на газоне на улице, на песке на пляже или в траве в лесу. Три ножки штатива всегда найдут плоскость.

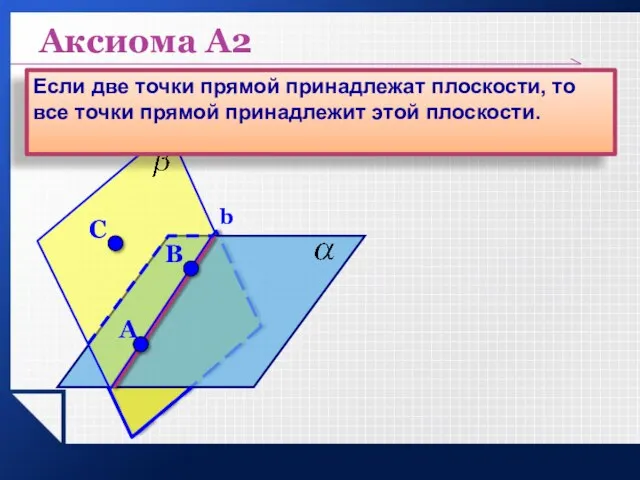
b
Аксиома А2
Если две точки прямой принадлежат плоскости, то все точки прямой принадлежит этой плоскости.

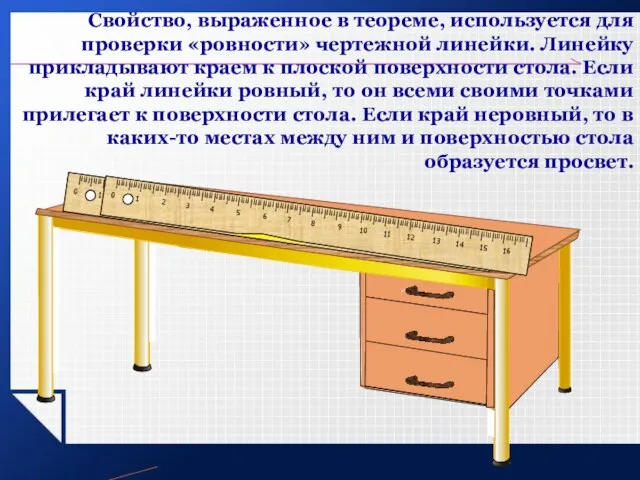
Свойство, выраженное в теореме, используется для проверки «ровности» чертежной линейки. Линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный, то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.

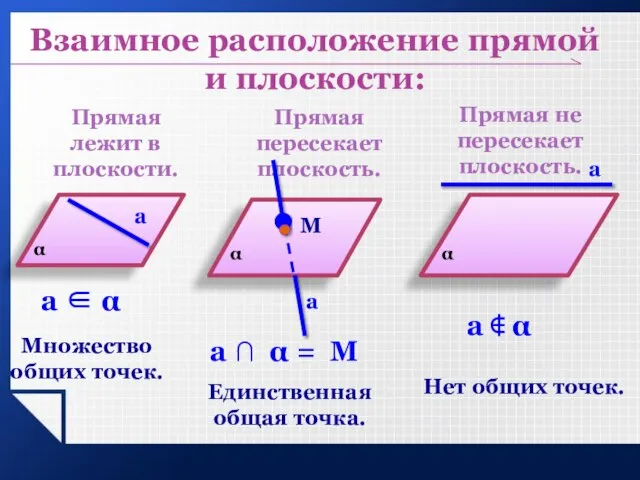
Прямая лежит в плоскости.
Прямая пересекает плоскость.
Прямая не пересекает плоскость.
Множество общих точек.
Единственная общая точка.
Нет общих точек.
α
а
α
а
М
α
а
а ∈ α
а ∩ α = М
а ∉ α
Взаимное расположение прямой и плоскости:

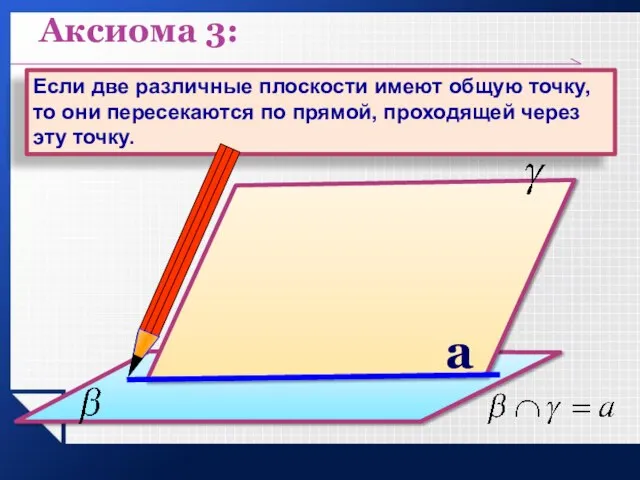
Аксиома 3:
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
a

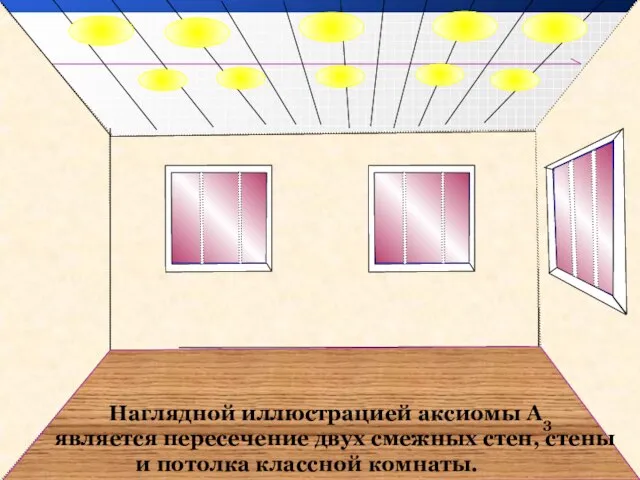
Наглядной иллюстрацией аксиомы А3
является пересечение двух смежных стен, стены и потолка классной комнаты.

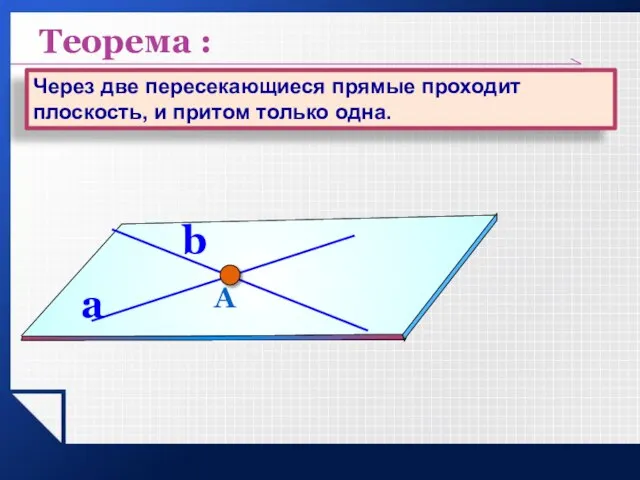
А
a
b
Теорема :
Через две пересекающиеся прямые проходит плоскость, и притом только одна.

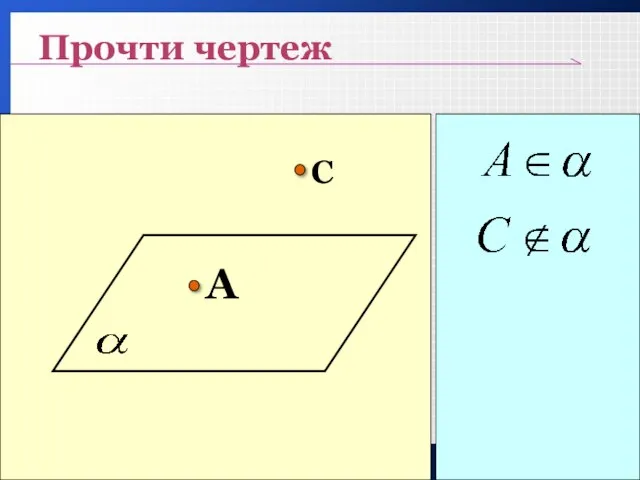
Прочти чертеж
A
С

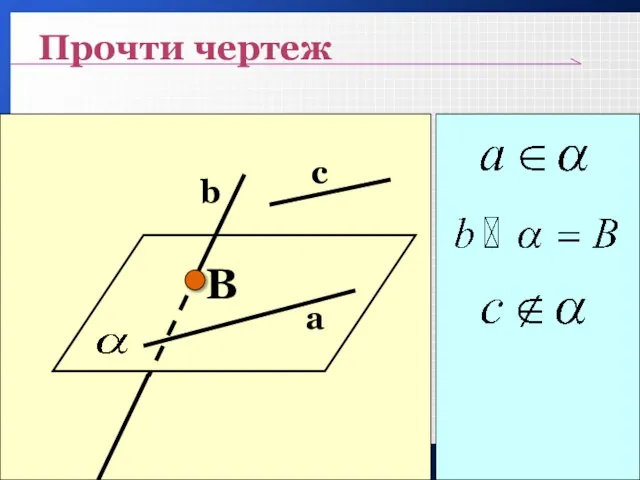
Прочти чертеж
B
c
b
a

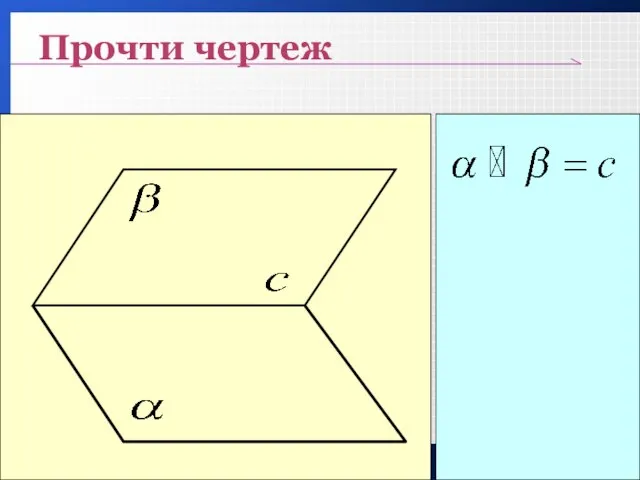
Прочти чертеж

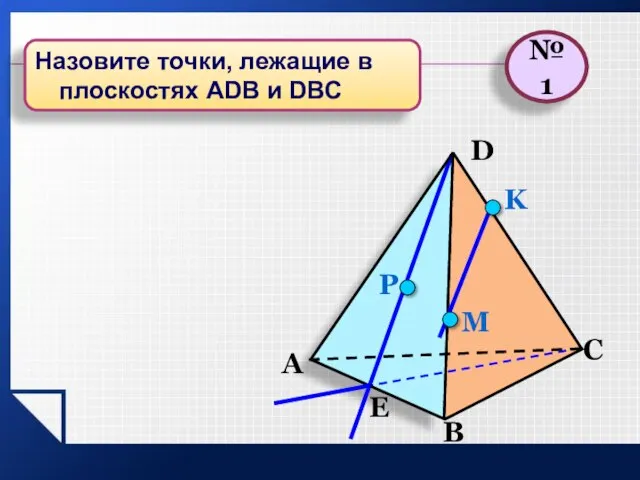
P
E
A
B
C
D
M
K
№1
Назовите точки, лежащие в плоскостях АDB и DBC

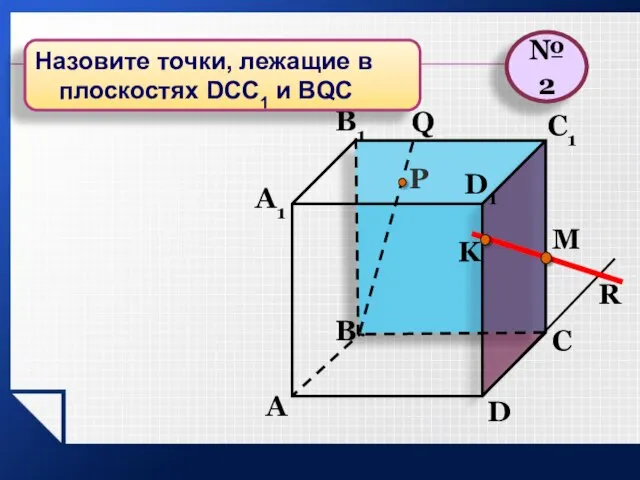
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
№2
Назовите точки, лежащие в плоскостях DCC1 и BQC

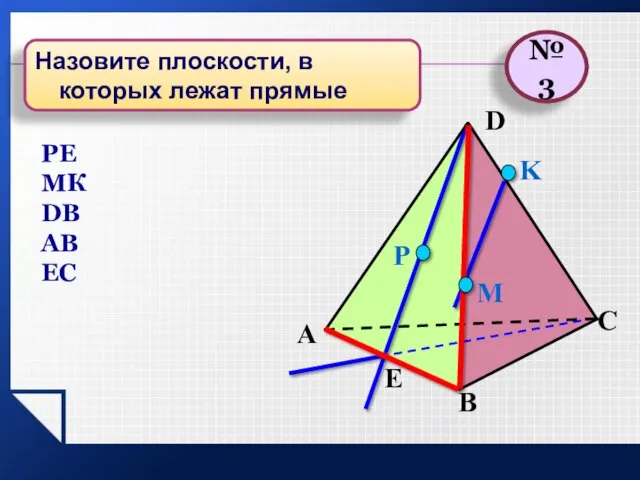
P
E
A
B
C
D
M
K
№3
Назовите плоскости, в которых лежат прямые
РЕ
МК
DB
AB
EC

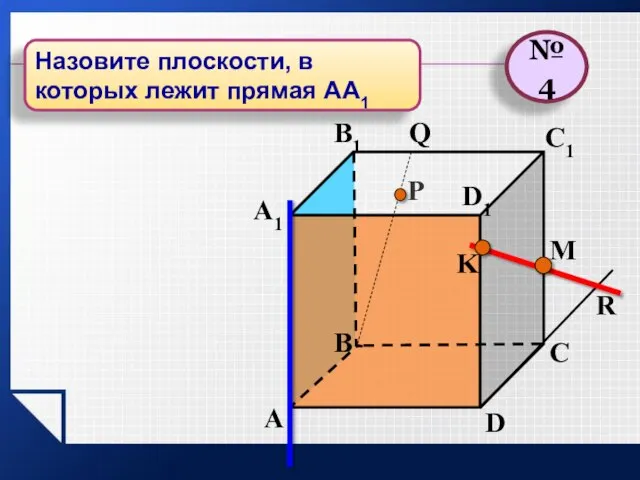
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
№4
Назовите плоскости, в которых лежит прямая АА1

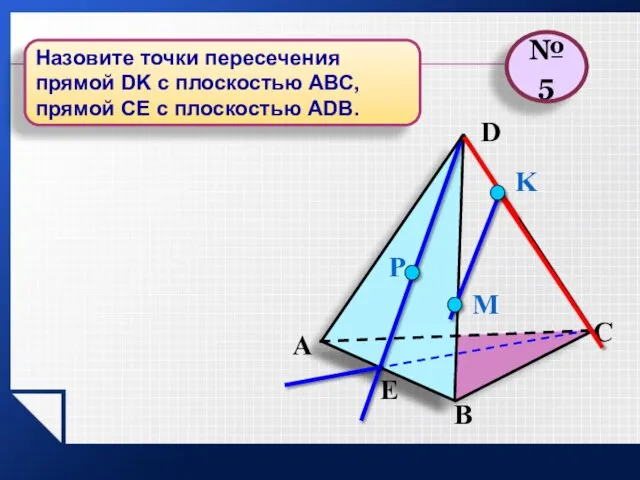
P
E
A
B
C
D
M
K
№5
Назовите точки пересечения прямой DK с плоскостью АВС,
прямой СЕ с плоскостью АDB.

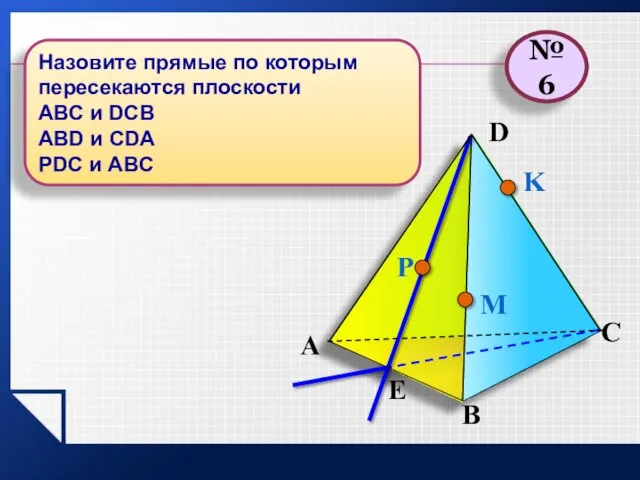
P
E
A
B
C
D
M
K
№6
Назовите прямые по которым пересекаются плоскости
АВС и DCB
ABD и CDA
PDC и ABC

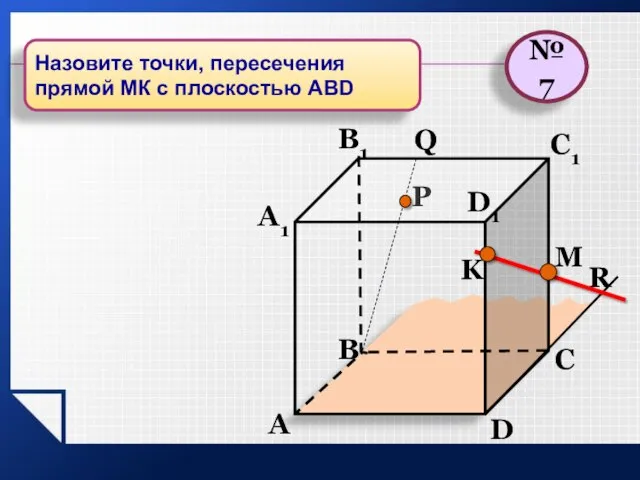
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
№7
Назовите точки, пересечения прямой МК с плоскостью АВD

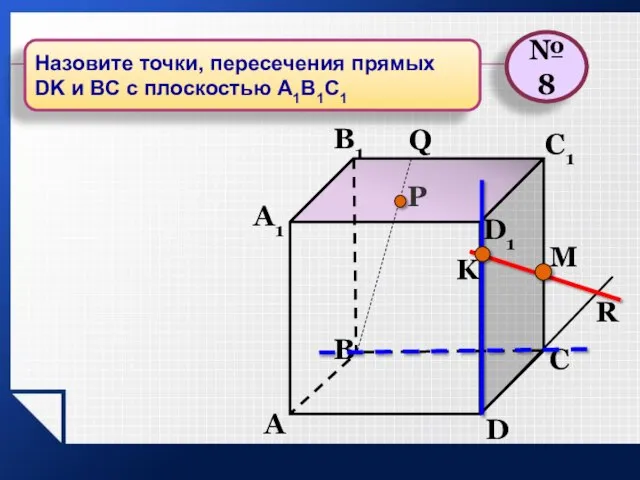
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
№8
Назовите точки, пересечения прямых DK и ВС с плоскостью А1В1С1

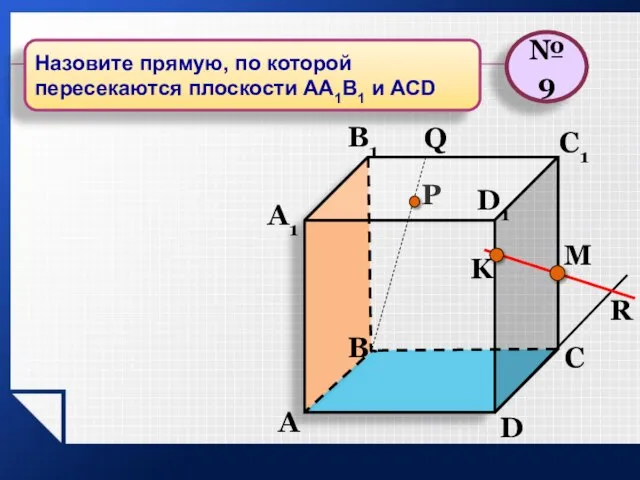
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
№9
Назовите прямую, по которой пересекаются плоскости АА1В1 и АСD

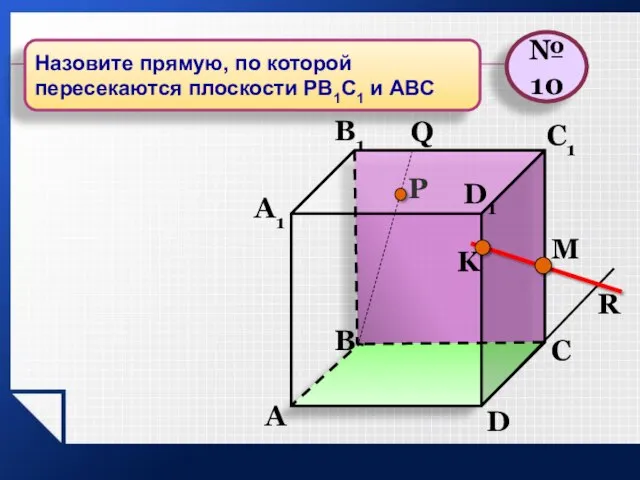
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
№10
Назовите прямую, по которой пересекаются плоскости PВ1C1 и ABC

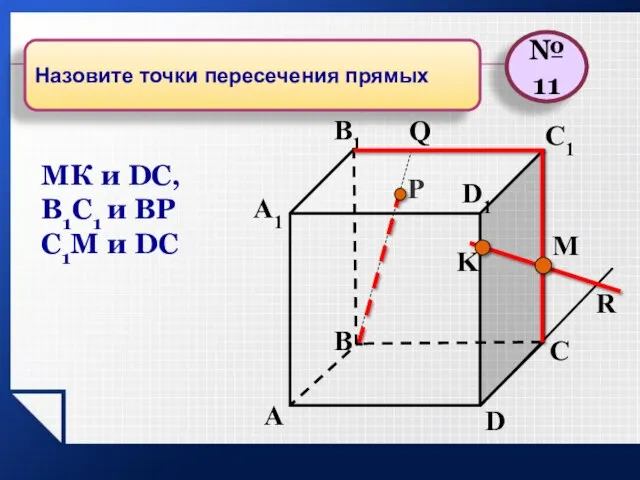
K
P
A
B
C
D
A1
B1
C1
D1
R
M
Q
МК и DC,
В1С1 и ВР
С1М и DC
№11
Назовите точки пересечения прямых