Меры связи, основанные на статистической зависимости. Коэффициент Юла

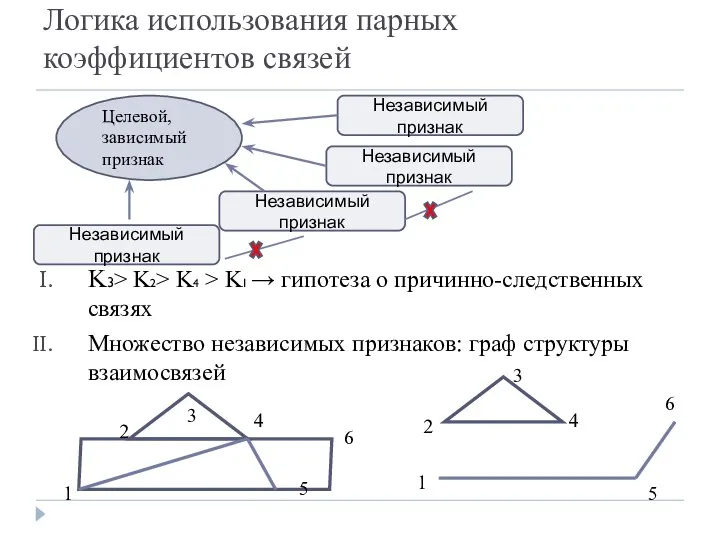
Логика использования парных коэффициентов связей
K3> K2> K4 > K1 → гипотеза о причинно-следственных связях
Множество независимых признаков: граф структуры взаимосвязей
Целевой,
зависимый
признак
Независимый признак
Независимый признак
Независимый признак
Независимый признак
2
1
1
2
3
3
4
4
5
5
6
6

Анализ данных в таблицах сопряженности 2х2
Например: опрошены студенты социологи
Есть ли статистическая закономерность между этими признаками?
Если наблюдается статистическая независимость, то …
доля магистров в группе «уверенных» должна равняться доле магистров в группе «неуверенных», т.е.
, т.е. a (d+b) = (a+c) d → ab = cd ; и a (c + b) = (a + d) c → ab = cd
ab - cd - мера отклонения от статистической независимости;
Знаменатель – для нормирования (изменения от – 1 до + 1)
Коэффициент Юла:

Свойства коэффициента Юла:
Q = 1, если с = 0 или d = 0
Q = - 1, если а = 0 или b = 0
Q = 0, если ab = cd,
т.е. наблюдается статистическая независимость
Q = 0,1397 ~ 0,14

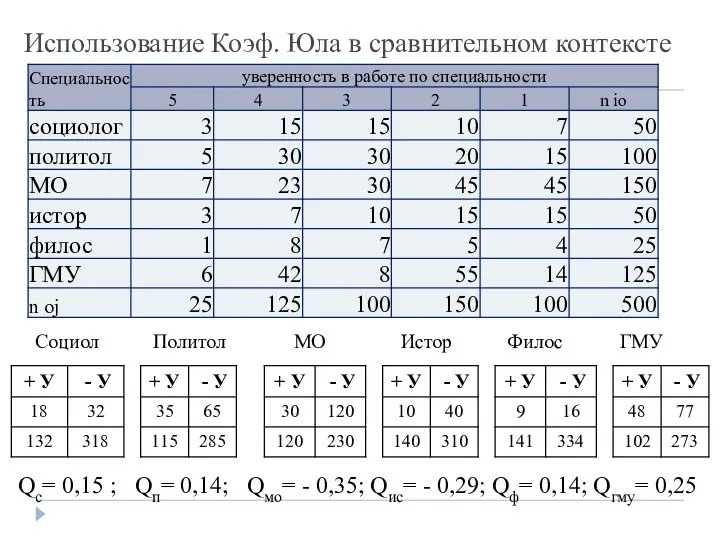
Использование Коэф. Юла в сравнительном контексте
Социол
Политол
МО
Истор
Филос
ГМУ
Qс= 0,15 ; Qп= 0,14; Qмо= - 0,35; Qис= - 0,29; Qф= 0,14; Qгму= 0,25

Сравнение по коэффициенту:
Qс= 0,15 ;
Qп= 0,14;
Qмо= - 0,35;
Qис= - 0,29;
Qф= 0,14;
Qгму= 0,25
Коэффициенты упорядочиваются по силе связи (без учета прямая или обратная зависимость), т.о.:
Qмо > Qис > Qгму > Qс > Qп > Qф
Связь (в данном контексте) – статистическая зависимость

Понятие детерминации для локальной связи
Если А, то В - правило детерминации:
одно свойство оказывает влияние на другое: А → В.
Например: Социолог → Уверенность в работе.
Характеристики детерминации:
Интенсивность : Емкость:
Для социологов: а = 18; a + d = 50; a + c = 150
I (C →У) = 36 %, С (С→ У) = 12 %
Интерпретация детерминации (схема):

Непосредственная – опосредованная связь
Qс= 0,15 – указывает статистическую независимость
для всех для девушек для юношей
Qс= 0,15 – ложное отсутствие корреляционной связи
4
3
2
1
5
6

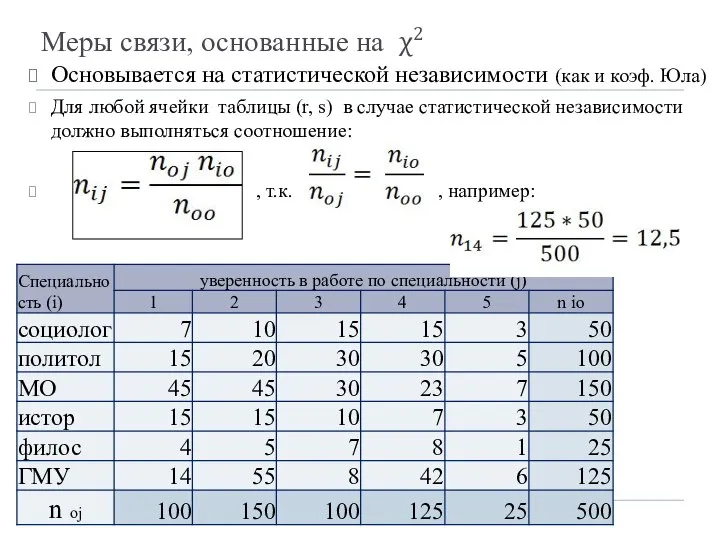
Меры связи, основанные на χ2
Основывается на статистической независимости (как и коэф. Юла)
Для любой ячейки таблицы (r, s) в случае статистической независимости должно выполняться соотношение:
, т.к. , например:

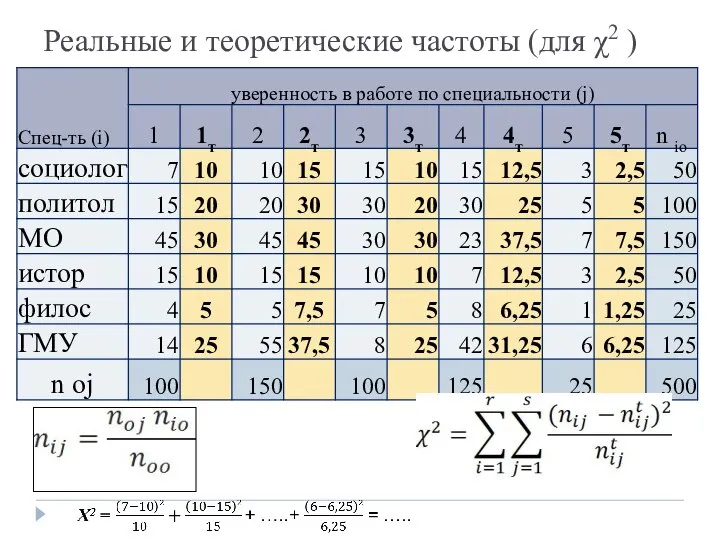
Реальные и теоретические частоты (для χ2 )

Коэффициент взаимной сопряженности Пирсона (на основе критерия Χ2)
Χ2t – табличное значение коэффициента (находим по таблице, при заданном уровне значимости (возможной ошибки α =0,1; 0,05;0,01) и числе степеней свободы (r-1) (s-1) (где r – число строк, s – число столбцов в таблице)
ВЫВОД о статистической значимости: Если χ2 > χ2t при заданном уровне значимости (возможной ошибки α =0,1; 0,05;0,01) и числе степеней свободы (r-1) (s-1) – признаки являются статистически зависимыми…
Наиболее часто используемый коэффициентов на основе распределения χ2 :
С – приближается к 0 или 1

Домашнее задание (на любом примере из исследования практикума):
Выявить локальные связи на основе использования коэффициента Юла. Описать результаты
Вычислить интенсивность и емкость детерминации для нескольких свойств (в этом же примере). Описать результаты.
Вычислить значение хи-квадрат и сравнить с табличным при различных уровнях значимости (НАЙТИ ТАБЛИЦУ ХИ-КВАДРАТ САМОСТОЯТЕЛЬНО). Описать результаты