Содержание
- 2. Есть ли общие признаки в содержании понятий? А- Студент В – Таракан; А- Студент В –
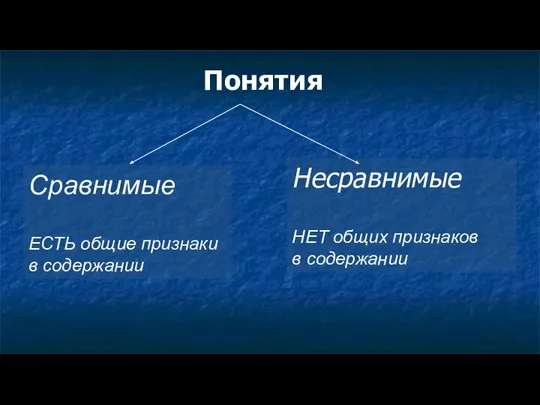
- 3. Понятия Сравнимые ЕСТЬ общие признаки в содержании Несравнимые НЕТ общих признаков в содержании
- 4. Несравнимые понятия Только философские категории Материальное – идеальное Конкретное – абстрактное Объективное - субъективное
- 5. Сравнимые понятия (есть общие признаки в содержании) Есть ли общие элементы в объеме?
- 6. Сравнимые понятия Совместимые ЕСТЬ общие признаки в содержании Несовместимые НЕТ общих признаков в содержании
- 7. Примеры А – студент В – таракан; А – успевающий студент В – неуспевающий студент Несовместимые
- 8. Совестимые понятия Тождественные (равнообъемные) Перекрещивающиеся Родо-видовые (подчиненные) А=В А В в А
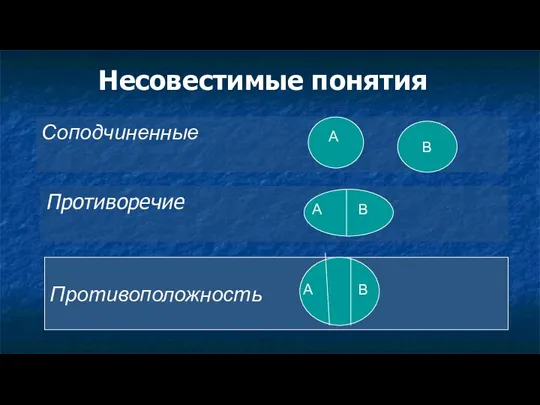
- 9. Несовестимые понятия Соподчиненные Противоречие Противоположность В А А В А В
- 10. Пример (задание № 2) Определить вид отношений между понятиями, изобразив их объемы при помощи кругов Эйлера
- 11. Определяем, есть ли единичные понятия Объемы единичных понятий изображаются точками.
- 12. Отношения определяются отдельно в каждой паре понятий Сначала определяем отношения в парах: 1-2; 1-3; 1-4
- 13. Это мы нарисовали объем понятия 1 – населенный пункт (понятие общее) 1
- 14. Является ли какой-то населенный пункт городом? ДА – значит понятия 1 и 2 совместимые (НЕТ -
- 15. Теперь будем выяснять, какой в данном случае вид совместимости ЛЮБОЙ ли населенный пункт – город?
- 16. НЕТ – значит это не тождественные понятия Теперь будем выяснять, являются они перекрещивающимися или подчиненными
- 17. Чем отличаются? Перекрещивающиеся Родо-видовые (подчиненные) А В в А
- 18. У подчиненного понятия В объем полностью входит в объем А У перекрещивающегося понятия В объем частично
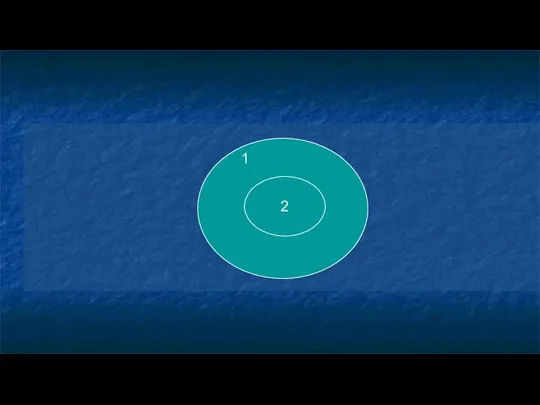
- 19. ЛЮБОЙ ли город является населенным пунктом? ДА - значит понятия 1 и 2 - ПОДЧИНЕННЫЕ
- 20. 2 1
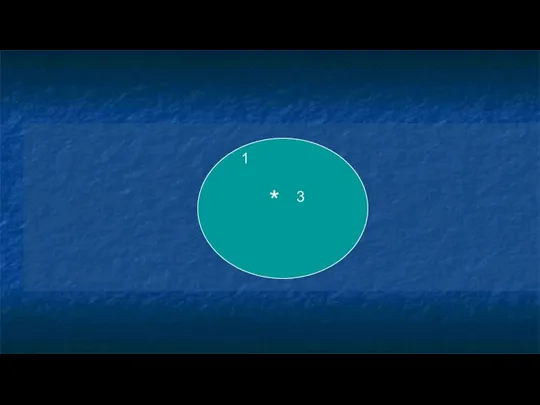
- 21. Работаем с понятиями 1 и 3: Является ли город Оренбург населенным пунктом? ДА - значит понятия
- 22. 1 * 3
- 23. Работаем с понятиями 1 и 4: Является ли какой-то городской житель населенным пунктом? НЕТ - значит
- 24. Выясняем, какой у нас вид несовместимости. Начинаем с самого простого варианта несовместимости – Противоречия
- 25. Если понятия 1 и 4 противоречащие, то 1 4
- 26. Это означает, что как только предмет не 1 (населенный пункт), то он является 4 (городским жителем)
- 27. НЕТ - значит это не противоречащие понятия Теперь выясним, являются они противоположными или соподчиненными
- 28. Выясним: В мире - населенный пункт, городской житель и что-то «среднее» между ними? В мире –
- 29. Понятия 1 и 4 – соподчиненные 1 4
- 30. Аналогично определяем отношения в парах: 2-3; 2-4 * 2 3 2 4 подчинение соподчинение
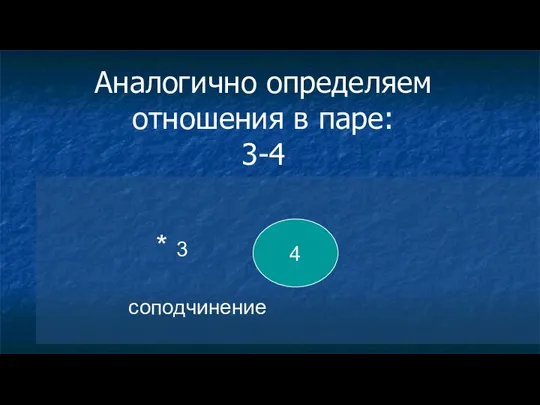
- 31. Аналогично определяем отношения в паре: 3-4 4 соподчинение * 3
- 32. ОБЩАЯ схема отношений между понятиями 4 * 3 1 2 * 3
- 33. § 4. Операции над понятиями Когда мы оперируем с понятием мы что-то делаем с его объемом
- 34. Операции над объемом понятия Объем Уменьшить Увеличить Оставить без изменения, но разбить на классы
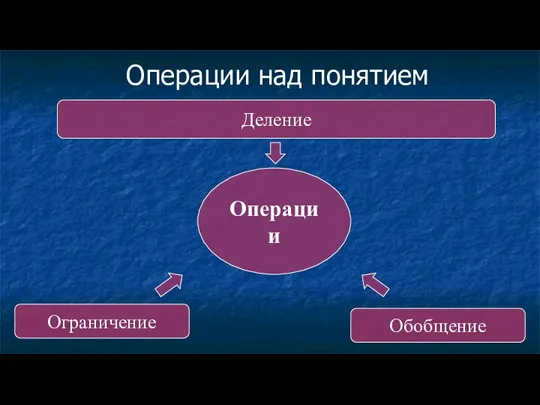
- 35. Операции над понятием Операции Ограничение Обобщение Деление
- 36. П.1. Ограничение понятия. Логическая операция над понятием, в результате которой объем понятия уменьшается путем добавления признаков
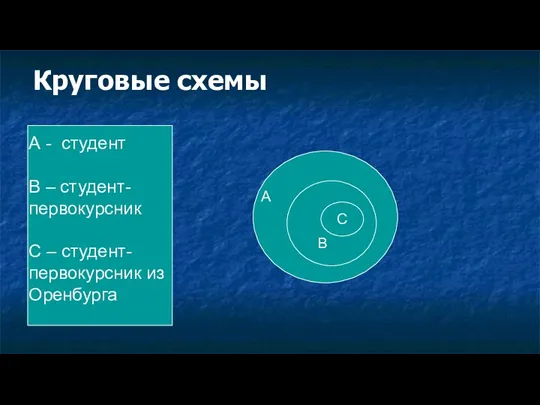
- 37. Круговые схемы А - студент В – студент- первокурсник С – студент-первокурсник из Оренбурга А В
- 38. Есть ли предел ограничения понятия? Есть Любое единичное понятие из объема исходного понятия
- 39. П.2. Обобщение понятия. Логическая операция над понятием, в результате которой объем понятия увеличивается путем отбрасывания части
- 40. Круговые схемы А –министерство финансов В – министерство С – орган государственной власти С В А
- 41. Есть ли предел обобщения понятия? Есть: ФИЛОСОФСКИЕ КАТЕГОРИИ
- 42. Пример. Обобщить понятие до предела, совершив 3 шага обощения. А - Студент В – Учащийся С
- 43. П.3. Деление понятия. Логическая операция над понятием, в результате которой объем понятия остается прежним, но разбивается
- 44. Виды деления: Деление на 2 класса Эти классы – противоречащие понятия Дихотомическое По видоизменению признака Деление
- 45. Дихотомическое деление: Деление всегда правильное Деление простое Достоинства Недостатки За один шаг деления могут получиться большие
- 46. Деление по видоизменению признака: За один шаг получаем нужные по объему классы Достоинства Недостатки Деление сложное
- 47. ЗАМЕЧАНИЕ: Закон обратного отношения справедлив только для логических объемов понятий. Закон обратного отношения не справедлив для
- 48. Правила деления: 2. Члены деления должны исключать друг друга 1. Деление должно производиться по одному основанию
- 49. Правила деления: - Не широким (не содержать пустых понятий среди членов деления) 4. Деление должно быть
- 51. Скачать презентацию









































 Презентация на тему Культурный человек
Презентация на тему Культурный человек  Самый уютный
Самый уютный Презентация на тему Конкурс ведущих
Презентация на тему Конкурс ведущих  Модель современной семьи
Модель современной семьи Взаимосвязь методов при изучении объектов природы - презентация к уроку Окружающий мир_
Взаимосвязь методов при изучении объектов природы - презентация к уроку Окружающий мир_ что делает человека человеком
что делает человека человеком Введение в современную теория социального мира. Лекция 1
Введение в современную теория социального мира. Лекция 1 Презентация на тему :«Тело человека» Выполнила ученица 4 «Б» класса Самарина Наталия
Презентация на тему :«Тело человека» Выполнила ученица 4 «Б» класса Самарина Наталия Нетворкинг. Урал Политический
Нетворкинг. Урал Политический Дальше - больше
Дальше - больше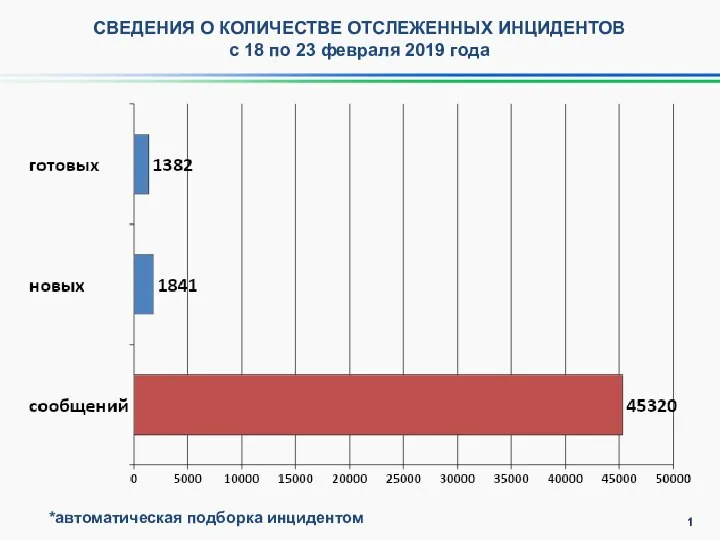 Сведения о количестве отслеженных инцидентов с 18 по 23 февраля 2019 года
Сведения о количестве отслеженных инцидентов с 18 по 23 февраля 2019 года Чудеса случаются. Социальный проект
Чудеса случаются. Социальный проект Презентация на тему Степ-аэробика
Презентация на тему Степ-аэробика  Социальная адаптированность
Социальная адаптированность Скандальные певцы
Скандальные певцы Тест по теме: «Социальная сфера»
Тест по теме: «Социальная сфера» Жители села Емельяновка участвуют в инициативном бюджетировании
Жители села Емельяновка участвуют в инициативном бюджетировании Минздрав предупреждает «ПРОКУРЕННЫЕ ДЕНЬГИ» автор проекта: Муравьев Алексей 10а класс Руководитель проекта:
Минздрав предупреждает «ПРОКУРЕННЫЕ ДЕНЬГИ» автор проекта: Муравьев Алексей 10а класс Руководитель проекта:  Презентация на тему Уголовная ответственность и преступление
Презентация на тему Уголовная ответственность и преступление  Личность и ее социализация
Личность и ее социализация Исследовательская работа Сладость – радость
Исследовательская работа Сладость – радость ПКОО Центр поддержки общественных инициатив Наш город
ПКОО Центр поддержки общественных инициатив Наш город «Солнышко» на ножке Выполнила ученица 4-в класса МОУ «Гимназия № 2» г.о.Балашиха мкр.Заря Бухтенкова Анастасия
«Солнышко» на ножке Выполнила ученица 4-в класса МОУ «Гимназия № 2» г.о.Балашиха мкр.Заря Бухтенкова Анастасия  Социальный волонтерский проект Твори добро
Социальный волонтерский проект Твори добро Презентация на тему Взаимопонимание в семье
Презентация на тему Взаимопонимание в семье  Общая характеристика готики
Общая характеристика готики Улучшение международных отношений
Улучшение международных отношений Семья в современном обществе
Семья в современном обществе