Слайд 2Актуальность
Оригами может быть интересно людям разного возраста. Во – первых, при помощи

оригами я получаю возможность создавать своими руками красивые геометрические фигуры из бумаги. Во - вторых, можно сделать оригинальный подарок близким или просто сделать что- то своими руками из бумаги - одно удовольствие. В - третьих, оригами это всегда красиво и оригинально.
Объект исследования - оригами
Предмет исследования - место оригами в рамках предмета «Геометрия».
Цель: вписать в модуль Сонобе тетраэдр.
Задачи исследования:
Изучить историю возникновения оригами, необходимый материал, приемы и технологию выполнения
Изучить лист бумаги, выполнив необходимые измерения.
Изучить каскадное вписывание многогранников.
Решить ряд задач.
Выполнить каскадное вписывание в модуль Сонобе тетраэдра и изготовить образцы изделий в технике оригами.
Гипотеза: Возможно, для того, чтобы поместить тетраэдр в модуль Сонобе, необходимо вычислить площадь необходимой бумаги для тетраэдра и для гексаэдра.
Слайд 3Красота и сложность многогранников.

Слайд 4Четыре многогранника символизировали в учении Платона четыре стихии:
икосаэдр-вода
октаэдр-воздух
куб-земля
тетраэдр-огонь

Слайд 5Правильных многогранников – 5.
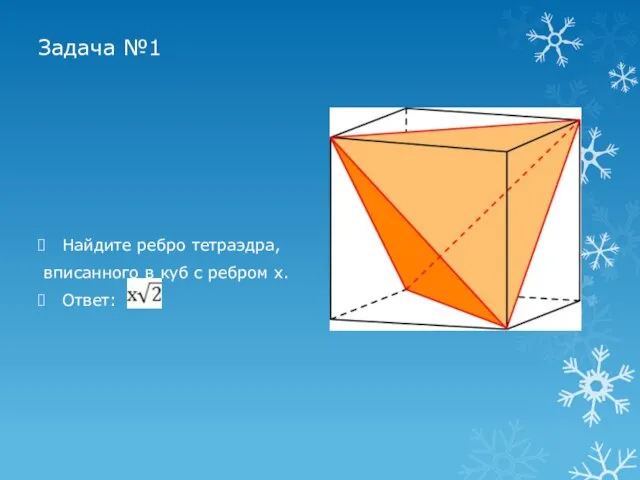
Слайд 7Задача №1
Найдите ребро тетраэдра,
вписанного в куб с ребром х.
Ответ:
Слайд 8Задача №2
Вычислить, используя 1 часть модуля Сонобе, отрезок равный ребру тетраэдра, если

берется квадрат из бумаги формата А4, т.е. сторона квадрата равна 21 см.
Ответ: 10,5 см.
Слайд 9Задача №3
Исследовать, какого размера нужно брать квадрат, чтобы ребро тетраэдра, вписанного в

искомый куб, составляло 10,5 см?
Ответ: Одного и того же размера квадратный лист.
Слайд 10Задача №4
Выполнить модель каскадного вписывания тетраэдра в гексаэдр, используя модуль Сонобе ,

метод оригами, результаты 1-3 задач.
Слайд 11Заключение
По результатам моего исследования можно сделать вывод, что гипотеза подтвердилась. Вывод: искусство

оригами тесно связано с математикой и может стать хорошей основой для ее изучения. Занимаясь оригами, я вышел за границы стандартной программы по математике и познакомился на практике с элементами геометрии в пространстве, а также выяснил, что оригами выступает как иллюстративный материал при проведении исследовательской работы.
С многогранниками мы постоянно встречаемся в нашей жизни – это древние Египетские пирамиды и кубики, которыми играют дети; объекты архитектуры и дизайна, природные кристаллы; вирусы, которые можно рассмотреть только в электронный микроскоп, прочные конструкции – шестиугольные соты, которые пчелы строили задолго до появления человека, книжные полки, вазы, письменный стол, шкатулки, коробочки, аквариумы, часы. Строить модели мне очень нравится, особенно используя оригами. Планирую продолжить моделирование каскадных вписываний многогранников.
Слайд 12Список литературы:
"Математика - Энциклопедия для детей" М.: Аванта +, 1998
Ковалев Ф.В. Золотое

сечение в живописи. К.: Высшая школа, 1989.
Стахов А. Коды золотой пропорции.
Смирнова И.М. В мире многогранников. - М.: Просвещение, 1995
Журнал «Наука и техника»
Журнал «Квант», 1973, № 8.
Журнал «Математика в школе», 1994, № 2; № 3.
http://ru.wikipedia.org
http://festival.1september.ru
http://images.yandex.ru
http://pedsovet.su
http://museum.ru
Материалы Википедии.












 Учебный курсдля учащихся 4 классов
Учебный курсдля учащихся 4 классов Теории творчества и креативности
Теории творчества и креативности Русская трапеза
Русская трапеза ?
? Экслибрис. Задание по прикладной композиции
Экслибрис. Задание по прикладной композиции Большие гонки
Большие гонки Умники и умницы
Умники и умницы Презентация на тему Внешнее и внутреннее строение насекомого
Презентация на тему Внешнее и внутреннее строение насекомого Формула сайта:Успешный интернет-магазин от А до Я
Формула сайта:Успешный интернет-магазин от А до Я Управление Росприроднадзора по Свердловской области ОАО Уральский центр энергосбережения и экологии Сохранение и обустройство
Управление Росприроднадзора по Свердловской области ОАО Уральский центр энергосбережения и экологии Сохранение и обустройство  Основы тайм-менеджмента
Основы тайм-менеджмента Экслибрис – искусство книжного знака
Экслибрис – искусство книжного знака Securities fraud
Securities fraud Цикл менеджмента. Планирование
Цикл менеджмента. Планирование История возникновения логарифмов
История возникновения логарифмов Was ist in Deutschland
Was ist in Deutschland  Особенности делового этикета в Японии
Особенности делового этикета в Японии Социально-значимая деятельность школьников
Социально-значимая деятельность школьников Добро пожаловать в наш Педагогический колледж! Университетский Педагогический колледж №16 – это авторитетное, современное, дина
Добро пожаловать в наш Педагогический колледж! Университетский Педагогический колледж №16 – это авторитетное, современное, дина Управление проектами Тема 1 – введение в управление проектами Проф., д.т.н. А.А. Дульзон
Управление проектами Тема 1 – введение в управление проектами Проф., д.т.н. А.А. Дульзон Метапредметный подход при преподавании математики: использование технологии метапредмета «Задача»
Метапредметный подход при преподавании математики: использование технологии метапредмета «Задача» Питание и органы пищеварения
Питание и органы пищеварения Презентация на тему Конструирование текстов, предложений (2 класс)
Презентация на тему Конструирование текстов, предложений (2 класс) Божественный идеал в религиях мира (Буддизм)
Божественный идеал в религиях мира (Буддизм) Организация и проведение мероприятий направленных на привлечение детей занятиями лыжным спортом
Организация и проведение мероприятий направленных на привлечение детей занятиями лыжным спортом Совы
Совы Вглядываясь в человека. Портрет
Вглядываясь в человека. Портрет Визитная карточка начальной школы ГУО «Гимназия №20 г.Минска»
Визитная карточка начальной школы ГУО «Гимназия №20 г.Минска»