Жук Анастасия Игоревна Системы дифференциальных уравнений в алгебре обобщенных функций Руководитель: кандидат физ.-мат. наук, д
Содержание
- 2. Содержание Актуальность. Поставленные цели. Объект и предмет исследования. Научная гипотеза. Основные результаты. Научная новизна. Положения, выносимые
- 3. Актуальность Системы дифференциальных уравнений в алгебре обобщенных функций описывают многие задачи физики, механики, техники, химии, биологии
- 4. Поставленные цели Описание решений системы дифференциальных уравнений в алгебре обобщенных функций. Исследование решений системы дифференциальных уравнений
- 5. Объект и предмет исследования Объектом исследования являются системы дифференциальных уравнений в алгебре обобщенных функций. Предметом исследования
- 6. Научная гипотеза Рассмотрим следующее нелинейное дифференциальное где – обобщенная производная функции ограниченной вариации. Предполагаем, что решением
- 7. Основные результаты Рассмотрим следующую задачу Коши на отрезке где произвольная функция, а функция ограниченной вариации на
- 8. Задаче (1) поставим в соответствие следующую конечно- разностную задачу с осреднением Здесь
- 9. Пусть произвольная фиксированная точка из отрезка Тогда можно представить в виде где Несложно видеть, что решение
- 10. Научная новизна Дана полная классификация решений системы дифференциальных уравнений в алгебре обобщенных функций.
- 11. Основные положения, выносимые на защиту Построение всех решений системы дифференциальных уравнений в алгебре обобщенных функций. Исследование
- 13. Скачать презентацию










 Презентация на тему Опасна ли гроза
Презентация на тему Опасна ли гроза Redaktiruemy_beydzh
Redaktiruemy_beydzh Физкультура. Виды плаванья
Физкультура. Виды плаванья О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС
О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС Письмо пером - за и против
Письмо пером - за и против Tin cup design
Tin cup design Транспорт. Виды транспорта
Транспорт. Виды транспорта Новый стандарт: обучаем и учимся
Новый стандарт: обучаем и учимся Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации
Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации Виды рабочей одежды
Виды рабочей одежды Я люблю тебя, Сакский район!
Я люблю тебя, Сакский район! Что такое значение?От П.Грайса к теории игр.
Что такое значение?От П.Грайса к теории игр. Тема лекции:«Прикладная информатика в табличном процессоре»
Тема лекции:«Прикладная информатика в табличном процессоре»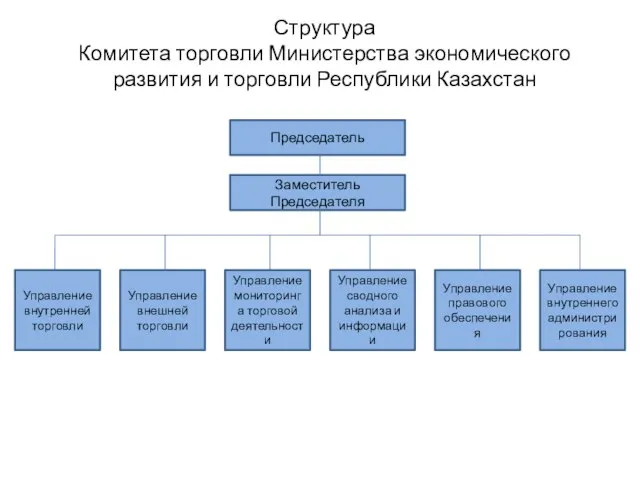 Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан
Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан Презентация на тему Информация в природе, обществе и технике
Презентация на тему Информация в природе, обществе и технике Основы коммуникативной компетентности педагогов
Основы коммуникативной компетентности педагогов Хочу отдыхать
Хочу отдыхать Урок по рассказам И.А. Бунина о любви
Урок по рассказам И.А. Бунина о любви Русская изба – поэтапное рисование
Русская изба – поэтапное рисование Известные люди Австрии
Известные люди Австрии 3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012
3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012 Викторина по произведениям А.П.Чехова « Смешные рассказы»
Викторина по произведениям А.П.Чехова « Смешные рассказы» Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г.
Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г. ЮТА (2)
ЮТА (2) Многообразие компьютеров
Многообразие компьютеров Похищение человека
Похищение человека Понятие и особенности административно правовой нормы
Понятие и особенности административно правовой нормы Техника мраморирования в современном дизайне
Техника мраморирования в современном дизайне