Урок алгебры в 10 классе по теме «Десятичные и натуральные логарифмы. Формула перехода к другому основанию» с применением ИКТ и п
Содержание
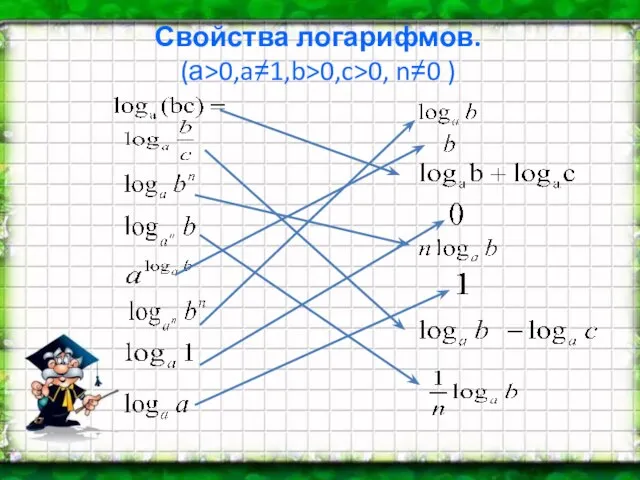
- 2. Свойства логарифмов. (а>0,a≠1,b>0,c>0, n≠0 ) :
- 3. Найдите значение выражений 4 - 0,5 -0,5 4 3 9 3 25 1 1 -2 2
- 4. Решите уравнение
- 5. Тренировочный тест 1.Вычислить: 0,3log0,32 – 5 – 4,91; 2) – 4,7; 3) – 3; 4) 2.
- 6. Проблема Обратите внимание - действия с логарифмами возможны только при одинаковых основаниях! А если основания разные!?
- 7. Переход к другому основанию Теорема Пусть дан логарифм loga b. Тогда для любого числа c такого,
- 8. Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg , т.е. log 10 m =
- 9. Воспользуемся сначала свойством Теперь перейдем к основанию 2
- 10. 2) Найдите значение выражения
- 11. 3)Найдите значение выражения , если Решение: Решение: Ответ: 12
- 12. Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году, хотя учитель
- 13. Происхождение термина натуральный логарифм Сначала может показаться, что поскольку наша система счисления имеет основание 10, то
- 14. е=2,718281828459045235360…. Саму константу впервые вычислил швейцарский математик Бернулли в ходе решения задачи о предельной величине процентного
- 15. Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его
- 16. Таблицы логарифмов Первые таблицы логарифмов были составлены швейцарским математиком Бюрги в 1590 году. Немного позднее таблицы
- 17. 1 группа 2 группа ; Задания для самостоятельной работы
- 18. Домашнее задание 1. Найдите 2. Вычислите:
- 20. Скачать презентацию
















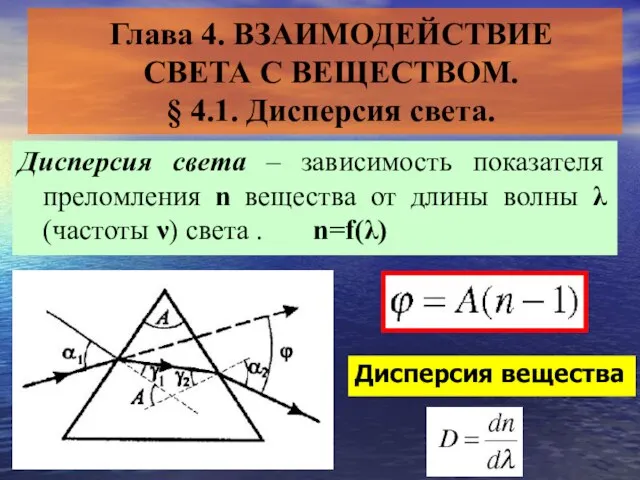 Презентация на тему Взаимодействие света с веществом Дисперсия света
Презентация на тему Взаимодействие света с веществом Дисперсия света
 Бизнес-план. Создание детского кафе Счастливое детство
Бизнес-план. Создание детского кафе Счастливое детство Современные и забытые виды спорта
Современные и забытые виды спорта СВЯЗЬ ИННОВАЦИИ СЕРВИС
СВЯЗЬ ИННОВАЦИИ СЕРВИС Аттестационная работа. Пищевые добавки и их влияние на организм
Аттестационная работа. Пищевые добавки и их влияние на организм ООО МДО Душанбе Сити
ООО МДО Душанбе Сити Понятие о профессии, специальности и квалификации работника. Классификация профессий
Понятие о профессии, специальности и квалификации работника. Классификация профессий Производственное здание и зем. участок
Производственное здание и зем. участок Эффекта не вмешивающегося свидетеля (синдром Дженовезе)
Эффекта не вмешивающегося свидетеля (синдром Дженовезе) Программа Intel «Путь к успеху» Итоги развития программы в 2008 году
Программа Intel «Путь к успеху» Итоги развития программы в 2008 году Стиль рококо. Художественное направление XVII – XVIII веков
Стиль рококо. Художественное направление XVII – XVIII веков Тема: Реальдо Коломбо: описание циркуляции крови через лёгкие.
Тема: Реальдо Коломбо: описание циркуляции крови через лёгкие. Инженер по гарантии. Шаблон документа
Инженер по гарантии. Шаблон документа МЕЛЬНИЦЫ Новейшая разработка в технологии ультратонкого измельчения
МЕЛЬНИЦЫ Новейшая разработка в технологии ультратонкого измельчения Комитет государственного имущества и приватизации Министерства финансов Республики Казахстан (КГИП)
Комитет государственного имущества и приватизации Министерства финансов Республики Казахстан (КГИП) Лекарственные препараты действующие на собирательные трубки
Лекарственные препараты действующие на собирательные трубки  Участник : Тугумбаев Алибек Айтуллаевич Открытие автокинотеатра «Sky cinema» в г. Астана.
Участник : Тугумбаев Алибек Айтуллаевич Открытие автокинотеатра «Sky cinema» в г. Астана. Гуманизм и новая наука
Гуманизм и новая наука Историческая справка Здание нашего детского сада было построено в 19.. году За это время здесь побывали и ясли и центр детского твор
Историческая справка Здание нашего детского сада было построено в 19.. году За это время здесь побывали и ясли и центр детского твор Общие принципы составления программ инфузионной терапии (ИТ) у детей Обедин А.Н. Ставрополь 2004
Общие принципы составления программ инфузионной терапии (ИТ) у детей Обедин А.Н. Ставрополь 2004 Удивительная вода
Удивительная вода Психология цвета
Психология цвета Техническая эксплуатация судовых АКБ
Техническая эксплуатация судовых АКБ Презентация на тему Математическая логика
Презентация на тему Математическая логика Организационно-правовые основы деятельности любительских объединений. Тема 6
Организационно-правовые основы деятельности любительских объединений. Тема 6 Создание республиканской медицинской информационной системы (РМИС)
Создание республиканской медицинской информационной системы (РМИС) Как правильно ставить цели и достигать их
Как правильно ставить цели и достигать их Оборотные средства предприятия
Оборотные средства предприятия