I научно-практическая конференция учащихся Заводского района г.Новокузнецка Секция математики Теорема Пифагора. Пифагоровы чи
Содержание
- 2. Оглавление: Введение Краткая биография Пифагора Теорема Пифагора Доказательство Бхаскары Пифагоровы числа Заключение
- 3. Введение: О Пифагоре и его жизни я услышала в пятом классе на уроке математики, и меня
- 4. Пребудет вечной истина, как скоро Её познает слабый человек! И ныне теорема Пифагора Верна, как и
- 6. Фалес Милетский – первый учитель Пифагора ионической натурфилософии и основатель милетской (ионийской) школы, с которой начинается
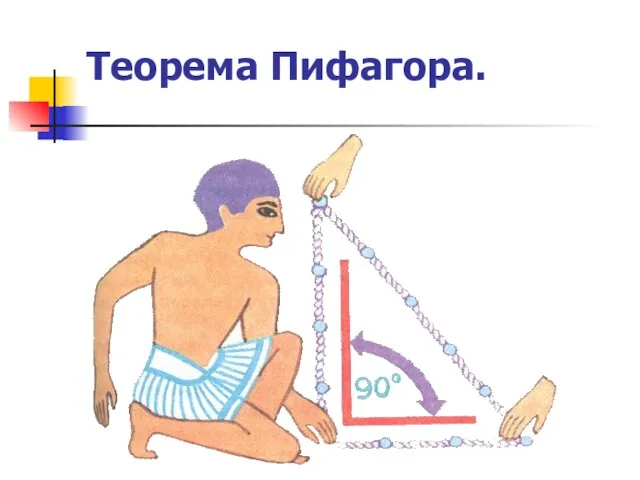
- 7. Теорема Пифагора.
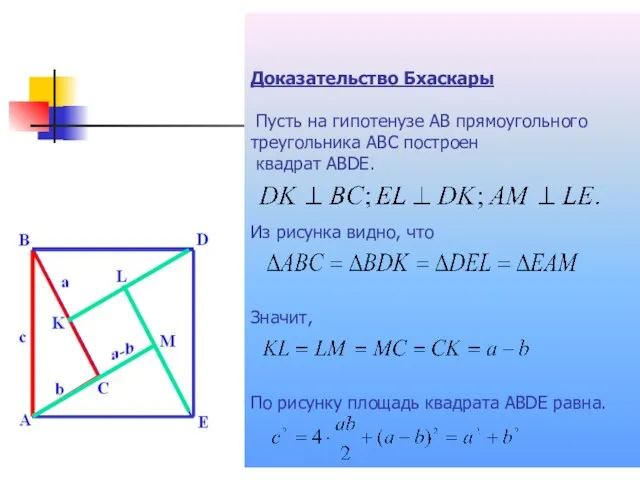
- 8. Доказательство Бхаскары Пусть на гипотенузе АВ прямоугольного треугольника АВС построен квадрат АВDЕ. Из рисунка видно, что
- 9. В древности доказательство теоремы было очень сложным и нерадивые ученики подбирали ей всякие нелестные клички: «ослиный
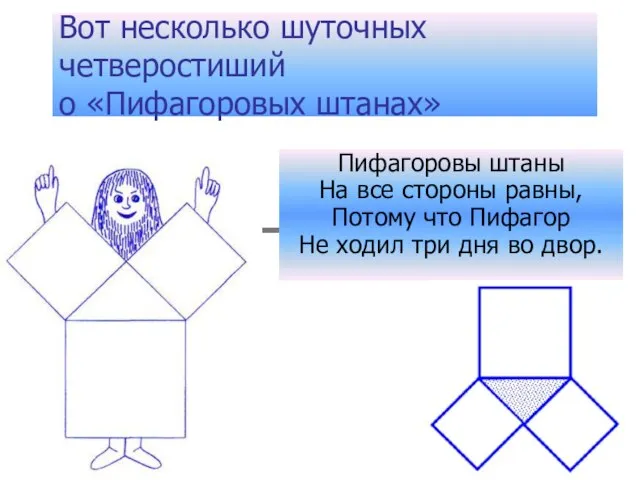
- 10. Вот несколько шуточных четверостиший о «Пифагоровых штанах» Пифагоровы штаны На все стороны равны, Потому что Пифагор
- 11. Пифагоровы штаны На все стороны равны. Чтобы это доказать, Нужно снять и показать
- 12. Пифагоровы числа. В математики пифагоровыми числами (пифагоровой тройкой) называется кортеж из трёх целых чисел (x, y,
- 13. Вот следующие Пифагоровы тройки: 3, 4, 5; 9+16=25. 5, 12, 13; 25+144=225. 7, 24, 25; 49+576=625.
- 14. При умножении каждого из чисел пифагоровой тройки на 2, 3, 4, 5 и т.д., мы получим
- 16. Заключение В результате моей работы мне удалось 1. Узнать о Пифагоре, его жизни, братстве Пифагорейцев. 2.
- 18. Скачать презентацию












 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»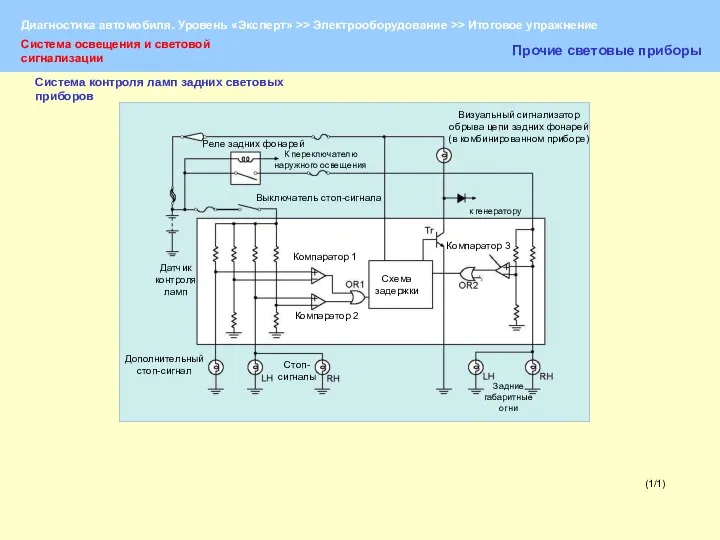 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс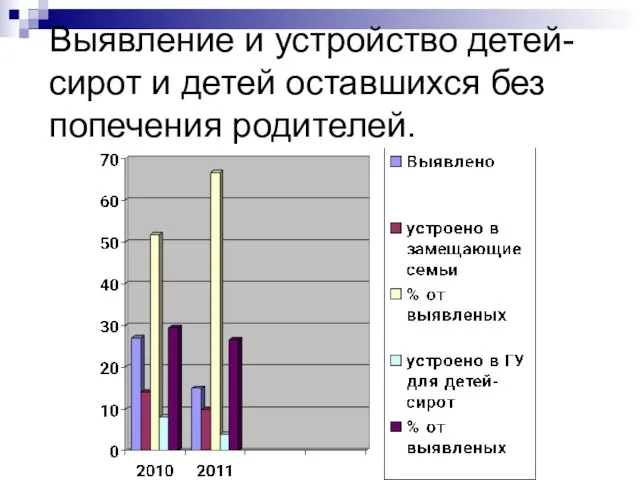 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства