?

Оглавление.
Информация о числе φ.
☹ Практики.
? Теоретики.
☺ Экспериментаторы.

Цель проекта:
φ
Развитие познавательной активности учащихся;
Формирование умений самостоятельной работы;
Способствовать развитию социально-коммуникативных качеств: общения работы в команде.

φ
Учебный проект «Золотое сечение» разработан для учащихся 10-11 классов по предмету математика, рассчитан на 4 часа.
Такая организационная форма учебной деятельности способствует развитию познавательной компетентности учащихся, навыков самостоятельной работы с большим объёмом информации и самообразовательной активности.
Известно, что развитие коммуникативных навыков учащихся будет проходить более эффективно, если применять нетрадиционные формы обучения: работа в малых группах, что создаёт оптимальные условия для активности творческих способностей каждого ученика. Совместная работа в группах способствует воспитанию чувства самоуважения, повышение личной уверенности в своих способностях.
Авторы данного проекта рекомендуют его использовать:
? для ведения факультативов;
? для внеурочной работы по предмету;
? в дни предметных декад.

Вопросы учебной темы.
φ
Знали ли учёные древнего мира и эпохи возрождения о числе ф? Есть ли этому подтверждение?
Существуют ли какие-то соотношения между частями тела человека?
Какой ряд чисел называется рядом Фибоначчи? Чем известен этот ряд?
Какие принципы формообразования в природе?
«Золотое сечение» и счастье – есть ли между ними какая-нибудь связь?
Используется ли в настоящее время число ф в науке и технике?

φ
С древних времён люди пытались понять, по каким законам развиваются природа и общество, почему тело и лицо одного человека кажутся гармоничнее и красивее, чем другого, каким закономерностям подчиняются произведения искусства…
На эти и многие другие вопросы может помочь ответить найденная ещё в глубокой древности закономерность – Золотое сечение.
Золотое сечение

φ
В математике пропорцией (лат. proportio) называют равенство двух отношений: a : b = c : d.
Отрезок прямой АВ можно разделить на две части следующими способами:
на две равные части – АВ : АС = АВ : ВС;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = c : a или с : a = a : b.
Геометрическое изображение золотой пропорции
Золотое сечение – гармоническая пропорция
a
b
c

φ
Если длина отрезка b равна 1, то значение нетрудно вычислить из уравнения
которое можно записать в виде обычного квадратного уравнения
Положительный корень этого уравнения равен
Это число одновременно выражает длину отрезка a и значение величины ф. Его десятичное разложение имеет лид 1,61803398... Если за единицу принять длину a, то длина b будет выражаться величиной, обратной ф, то есть 1/ф. Любопытно, что 1/ф = 0,61803398... Число ф — единственное положительное число, которое переходит » обратное ему при вычитании единицы.
Подобно числу л, ф можно представить в виде суммы бесконечного ряда многими способами. Предельная простота следующих двух примеров еще раз подчеркивает фундаментальный характер ф:

φ
Направления работы
Создаются группы:
☹ практики
? теоретики
☺ экспериментаторы

Цели практиков:
1. Формирование умений действовать самостоятельно;
2.Расширение умений и навыков работы с циркулем и линейкой.

φ
φ
☹ практики
Решение задач, связанных с числом φ:
1. Деление отрезка прямой по золотому сечению.
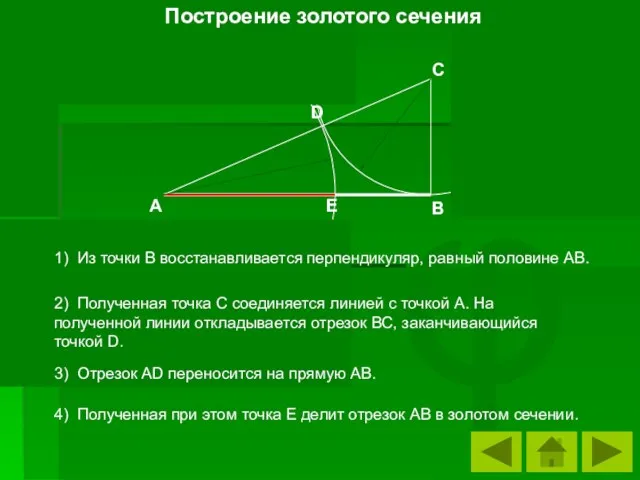
2. Построение пентаграмм.
3. Построение логарифмической спирали.
Деятельность
группы:

Построение золотого сечения.
Как же построить это «золотое сечение»?

φ
A
B
C
D
E
4) Полученная при этом точка Е делит отрезок АВ в золотом сечении.
1) Из точки В восстанавливается перпендикуляр, равный половине АВ.
2) Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D.
3) Отрезок AD переносится на прямую АВ.
Построение золотого сечения

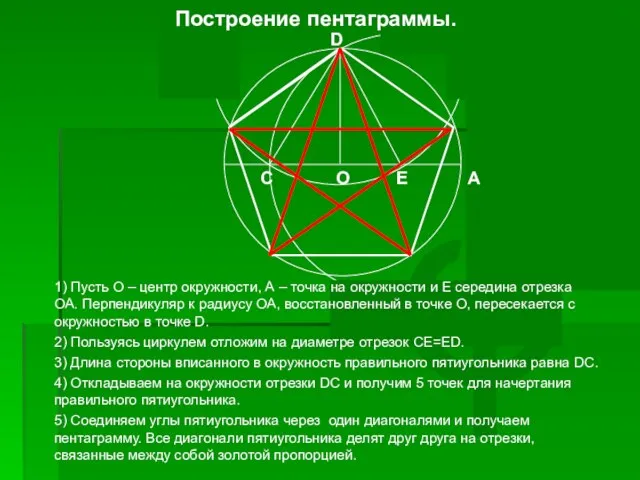
Построение пентаграммы.
Как же построить пентаграмму?

φ
E
A
O
C
D
1) Пусть О – центр окружности, А – точка на окружности и Е середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D.
2) Пользуясь циркулем отложим на диаметре отрезок CЕ=ЕD.
3) Длина стороны вписанного в окружность правильного пятиугольника равна DC.
4) Откладываем на окружности отрезки DC и получим 5 точек для начертания правильного пятиугольника.
5) Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Построение пентаграммы.

φ
Измерив и сопоставив отрезки, составляющие звезду, мы пришли к следующим выводам:
А
В
С
D
Какая зависимость между числом «фи» и пентаграммой?
1) Все диагонали прямоугольника делят друг друга на отрезки, связанные между собой золотой пропорцией
2) Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36 градусов при вершине, а основание, отложенное на боковую сторону, делят её в пропорции золотого сечения

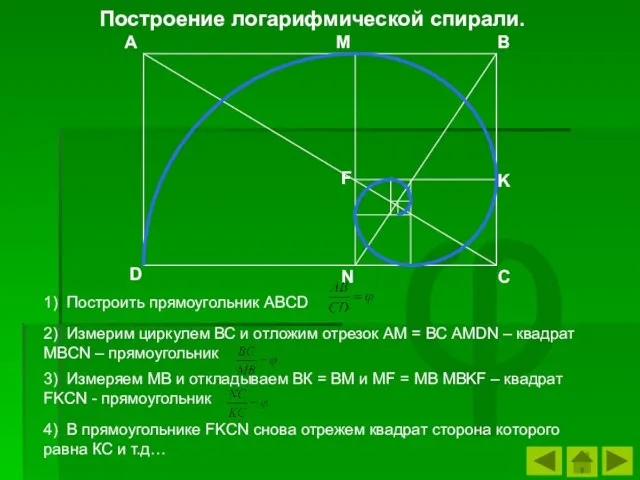
Построение логарифмической спирали.
Как же построить логарифмическую спираль?

φ
А
M
B
K
C
N
D
F
1) Построить прямоугольник ABCD
2) Измерим циркулем ВС и отложим отрезок АМ = ВС AMDN – квадрат MBCN – прямоугольник
3) Измеряем МВ и откладываем ВК = ВМ и MF = MB MBKF – квадрат FKCN - прямоугольник
4) В прямоугольнике FKCN снова отрежем квадрат сторона которого равна КС и т.д…
Построение логарифмической спирали.

φ
Логарифмическая спираль в природе
Логарифмическая спираль – единственный тип спирали, не меняющий своей формы при увеличении размеров. Это свойство объясняет, почему логарифмическая спираль так часто встречается в природе.
Например по мере роста моллюска Nautilus, раковина его, разделённая внутренними перегородками, увеличивается в своих размерах, закручиваясь по логарифмической спирали. При этом домик его не меняет формы: если центральную часть раковины посмотреть под микроскопом, мы увидим в точности такую же спираль, какая получилась бы, если бы раковина выросла до размеров галактики и мы разглядывали бы её с большого расстояния.

Вывод:
С помощью циркуля и линейки можно построить золотое сечение.

Цели теоретиков:
1. Формирование умений действовать самостоятельно;
2. Способствовать развитию социально – коммуникативных качеств;
3. Умение пользоваться различными источниками информации.

φ
? теоретики
1. Составление справки по истории возникновения числа φ.
2. Число φ в пропорциях человеческого тела.
3. Ряд Фибоначчи.
4. Золотое сечение и счастье – есть ли между ними связь.
5. Оформление итогов работы в виде:
- буклета; - реферата; - презентации
Деятельность
группы:

φ
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
1. История золотого сечения.

φ
Динамические прямоугольники
Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
Античный циркуль золотого сечения

φ
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).

φ
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов.
Американский математик Марк Барр 95 лет назад предложил называть отношение двух отрезков, образующих золотое сечение буквой φ.
Буква φ – первая греческая буква в имени великого Фидия, который по преданию, часто использовал золотое сечение в своих скульптурах.

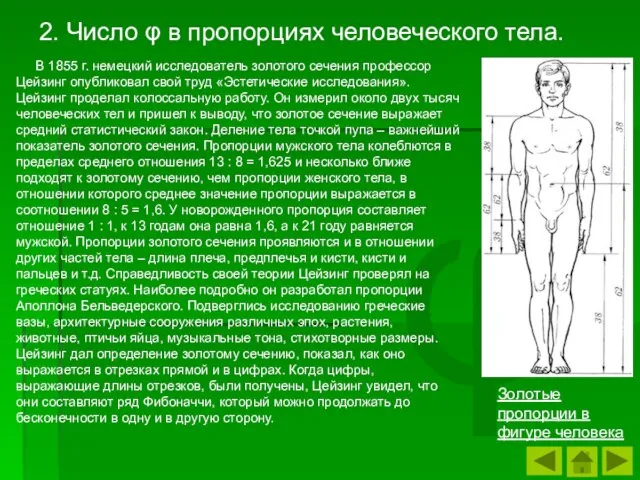
φ
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д. Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону.
Золотые пропорции в фигуре человека
2. Число φ в пропорциях человеческого тела.

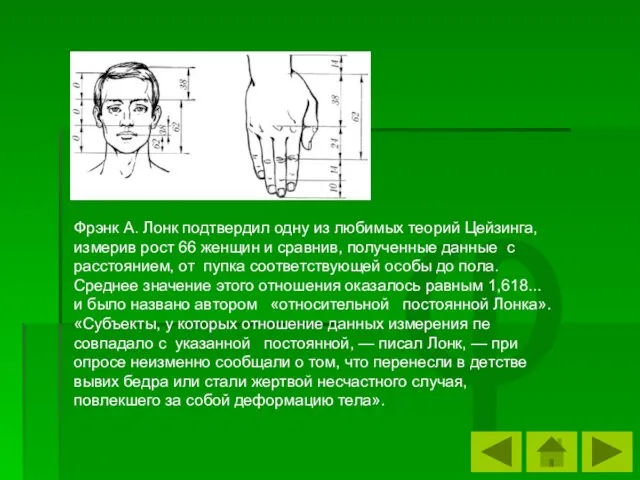
φ
Фрэнк А. Лонк подтвердил одну из любимых теорий Цейзинга, измерив рост 66 женщин и сравнив, полученные данные с расстоянием, от пупка соответствующей особы до пола. Среднее значение этого отношения оказалось равным 1,618... и было названо автором «относительной постоянной Лонка». «Субъекты, у которых отношение данных измерения пе совпадало с указанной постоянной, — писал Лонк, — при опросе неизменно сообщали о том, что перенесли в детстве вывих бедра или стали жертвой несчастного случая, повлекшего за собой деформацию тела».

φ
3. Ряд Фибоначчи.
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12и т.д.
Пары кроликов 0 1 1 2 3 5 8 13 21 34 58 91 144 и т.д.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.
Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16...

φ
Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.

φ
Испокон веку люди пытаются дать определение понятию «счастье», выявить какие- то общие «элементы», из которых оно слагается. Удаётся такой анализ плохо, потому что у каждого своё представление о счастье, да и переменчиво оно, хотя каждый, пожалуй, может вполне точно сказать, счастлив ли он. Этим и пользуются социологи, включая в свои анкеты вопрос о счастье.. Чаще, правда, он формируется как удовлетворённость своей жизнью или работой.
Изучая по данным опросов факторы, влияющие на ощущение счастья, исследователи задались вопросом о количественном соотношении счастливых и несчасливых людей. Анализ как отечественных, так и зарубежных данных показал, что численность удовлетворённых и неудовлетворённых своими обстоятельствами людей подчиняется пропорциям знаменитого «золотого сечения». По результатам опроса оказалось, что счастливыми считают себя 63% опрошенных. Поразительная цифра, ибо золотое сечение приходится на 62%.
Исследователи делают вывод, что, по- видимому, соотношение между счастливыми и несчастливыми не случайно, а подчинено общим структурным закономерностям, свойственным природным и в том числе биологическим объектам. Это – принципиально важное положение, поскольку открывает путь к теоретически обоснованной социальной диагностике и социальному проектированию.
4. "ЗОЛОТОЕ СЕЧЕНИЕ" и счастье

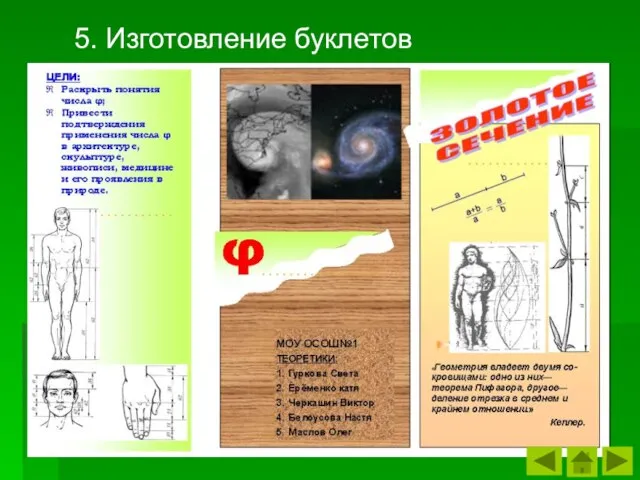
5. Изготовление буклетов

Мы узнали, что закономерности золотого сечения были известны с древних времён и использовалась в науке и искусстве.
Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Выводы:

Цели экспериментаторов:
1. Формирование умений действовать самостоятельно.

φ
☺ экспериментаторы
1. Проверка соответствия пропорций человеческого тела «золотому сечению».
Результаты измерения занести в таблицу:
Деятельность
группы:
С
B
A
2. Провести вычисления по формуле.
3. Сделать выводы о соответствии мужчин и женщин к «золотому сечению», где φ≈1,6

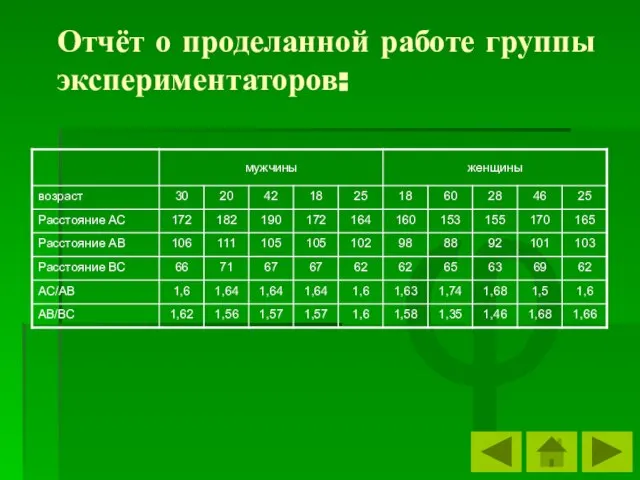
φ
Отчёт о проделанной работе группы экспериментаторов:

φ
В эпоху Возрождения и в настоящее время пропорции человеческого тела остаются гармоничными и основные анатомические точки делят тело человека в «золотой пропорции».
Пропорции мужчин ближе к «золотому сечению»
Человеческое тело ближе к «золотой пропорции» в среднем возрасте.
Выводы:

φ
ПРОВЕРЬ СЕБЯ
проект "ЗОЛОТОЕ СЕЧЕНИЕ"

Вопрос:
Выбери из данного ряда чисел число, значение которого равно числу φ:
1,68… 1,32…
2,56…
1
φ

φ
Вопрос:
Выбери пропорцию, соответсвующую «золотому сечению»:
АС/АВ = СВ/АС
АВ/АС = АС/ВС
АВ/АС = СВ/АС
А В С
2

φ
Вопрос:
Выбери значение длин отрезков, находящихся в «золотой пропорции»:
АВ = 5 см, ВС = 2 см
АВ = 24 см, ВС = 15 см
АВ = 48 см, ВС = 30 см
А В С
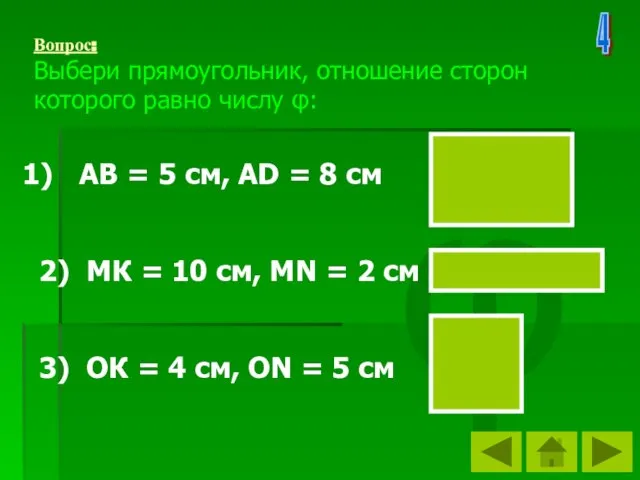
3

φ
Вопрос:
Выбери прямоугольник, отношение сторон которого равно числу φ:
АВ = 5 см, АD = 8 см
2) МК = 10 см, МN = 2 см
3) ОК = 4 см, ON = 5 см
4

Вопрос:
Буква φ , первая буква имени физика, который был…. :
астрономом
математиком скульптором
5
φ

φ
ПРАВИЛЬНЫЕ ОТВЕТЫ: