Царева Алина Александровна Кинематическое и динамическое моделирование плоских механизмов в системе Mathematica Руководитель: канд

Содержание
Актуальность.
Поставленные цели.
Объект и предмет исследования.
Научная гипотеза.
Основные результаты.
Научная новизна.
Положения, выносимые на защиту.

Актуальность
Одной из фундаментальных наиболее сложных и дисциплин, изучаемых студентами многих вузов, является теоретическая механика. При решении задач механики различного типа, возникает естественная необходимость корректной визуализации и отображения элементов конструкций, траекторий движений материальных точек и тел, числовых данных, а также в экономии времени на численных расчетах.
Актуальной проблемой на данном этапе является возможность использования пакетов компьютерной математики и механики применительно к моделированию и анализу полученных данных. Именно поэтому данная работа посвящена кинематическому и динамическому моделированию плоских механизмов, а также разработке электронного учебно-методического комплекса по теоретической механике на базе полученных результатов в системе Mathematica.

Поставленные цели
создание математических моделей основных задач механики, кинематических и динамических моделей плоских механизмов;
расчет и создание генераций схем и условий для индивидуальных заданий;
построение математических моделей движений материальных точек;
создание анимаций различных видов движения;
интеграция полученных результатов для разработки электронного учебно-методического комплекса
Внедрение разработанного курса в справочную систему пакета Mathematica

Объект и предмет исследования
Объектом исследования являются кинематические и динамические характеристики плоских механизмов, математическое моделирование, а также внутренняя структура справочной системы пакета Mathematica.

Научная гипотеза
Зависимость координат точки М от времени можно представить в виде:
Координата является одним из решений уравнения

Основные результаты
Построение математических моделей в системе Mathematica
При построении математических моделей были составлены уравнения, описывающие траектории движения, а также положение точек на плоских механизмах и самих механизмов. Данные уравнения были запрограммированы в пакете Mathematica:
gr=Graphics[{RGBColor[0,0,1],Thickness[0.004],Line[Table[{d Cos[p t]+r2 Cos[-(p t) r1/r2+p t] ,d Sin[p t]+r2 Sin[-(p t) r1/r2+p t]},{p,0,1,1/50}]]}]//.subst6;

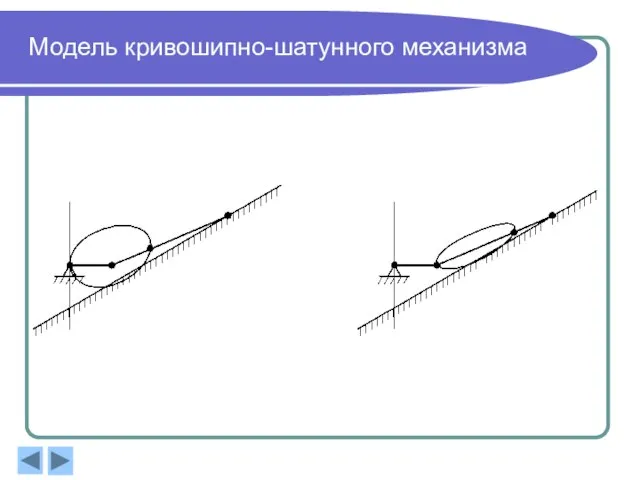
Анимация движения и построение траекторий выполняются на основании кинематических уравнений, описывающих зависимость координат характерных точек механизмов от времени. Это позволяет управлять анимацией, задавая в окнах ввода геометрические параметры, определяющие положение рассматриваемой точки на звене механической системы.
Для анимации движения, следует составить кинематические уравнения для точки А, в которой коленчатый вал соединяется с шатуном, и точки В, являющейся другим концом шатуна, в которой находится поршень, движущийся по наклонной направляющей. Также необходимо задать кинематические уравнения для построения траектории движения точки М, расположенной на шатуне АВ. Модель механизма, с описанной траекторией точки различным образом расположенной на звене плоского механизма, представлена на рисунке:
Анимация движения и построение траекторий

Модель кривошипно-шатунного механизма

Генерация индивидуальных заданий
Содержание учебного комплекса составляют текстовые ячейки с формулировкой постановки задачи, а также кнопки типа ButtonBox, позволяющие задать графическую схему совместно с числовыми данными.
Генерация схемы осуществляется случайным образом на основании восьми базовых графических объектов и экспортируется в графический файл с расширением JPEG
Числовые данные выбираются из определенного диапазона, ограниченного предельными значениями необходимых данных для элементов схемы, и автоматически добавляются в графический файл.
В ходе генерации графического и численного условий индивидуальных практических заданий осуществляется идентификация студента.

Научная новизна
Построены кинематические и динамические модели плоских механизмов

Основные положения, выносимые на защиту
Кинематическое и динамическое моделирование плоских механизмов
создание математических моделей основных задач механики
расчет и создание генераций схем и условий для индивидуальных заданий;
построение математических моделей движений материальных точек;
создание анимаций различных видов движения