Слайд 2«Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо

важнее. Политика существует только для данного момента, а уравнения будут существовать вечно»
А. Эйнштейн
Слайд 3
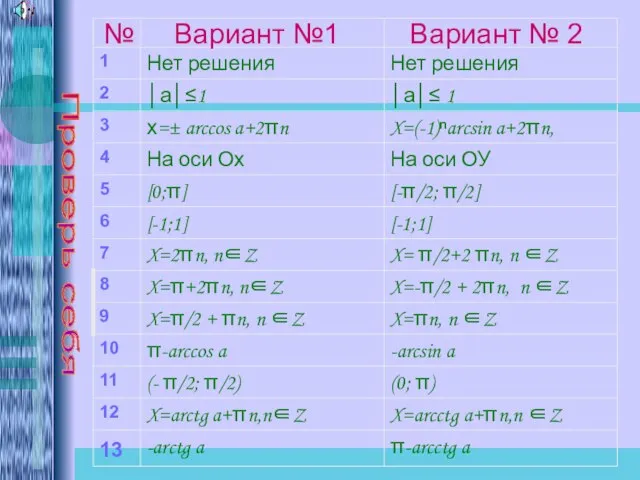
№ Вариант №1 Вариант № 2
Проверь себя
Слайд 4«Дороги не те знания, которые откладываются в мозгу, как жир, дороги те,

которые превращаются в умственные мышцы»
Герберт Спенсер
Слайд 5Метод, введения новой переменной
2sin²x-5sinx+2=0
Решение.
Пусть sinx=a (│a│≤1). 2а²-5а +2 =0,
D=9, a₁=2, не удовлетворяет

условию│a│≤1.
а₂=1/2.
Отсюда sinx=1/2, x=(-1)ⁿ π/6+πn, n∈Z.
Ответ: x=(-1)ⁿ π/6+πn, n∈Z.
Слайд 6Метод разложения на множители
2 sinx cos 5x – cos 5x =0.
Решение.
сos 5x(2sinx-1)=0.
Произведение

равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом не теряет смысла.
cos 5x =0 или sinx = 1/2,
5x =π/2 + πk, x = (-1)ⁿ π/6 + πn, n∈Z.
x = π/10 + πk/5, k∈Z.
Ответ: x = π/10 + πk/5, k∈Z;
x = (-1)ⁿ π/6 + πn, n∈Z.
Слайд 7 Однородное уравнение 1степени.
sin2x+cos2x=0.
Решение.
Разделим обе части уравнения почленно на cos2x. (если cos2x=0,

то и sin2x=0, а это невозможно, так как cos2x и sin2x обращаются в нуль в различных точках.)
Получим: tg2x+1=0, tg2x=-1, 2x=arctg(-1)+πn, 2x=-π\4+πn, x=-π\8+πn\2.
Ответ: x=-π\8+πn\2.
Слайд 8Однородное уравнение
2 степени
3sin²x + sin x cos x = 2 cos²x.
Решение.
Однородное

тригонометрическое уравнение 2 степени. Разделим почленно обе части уравнения на cos²x, где cos²x ≠ 0, (если cos²x=0, то и sin²x=0, что противоречит основному тригонометрическому тождеству cos²x + sin²x=1).
Получим 3tg²x + tg x – 2 = 0.Пусть tg x = a, тогда имеем
3а² + a – 2=0,
D = 25, a₁=-1, a₂= 2/3.
Отсюда tgx = -1, x = arctg (-1) +πn, n∈Z, x= - π/4 + πn, n∈Z;
tg x = 2/3, x = arctg 2/3 + πk, k∈Z.
Ответ: x= - π/4 + πn, n∈Z;
x = arctg 2/3 + πk, k∈Z.
Слайд 9Уравнение acos x + bsin x = c,
где abc ≠ 0
√3

cos x + sin x = 2
Решение.
a= √3, b =1, c = √a² + b² = √3+1=2.
√3/2 cos x + ½ sin x =1,
cos π/6 cos x + sin π/6 sin x =1, cos (x - π/6) =1,
x - π/6 = 2 πn, n∈Z,x= π/6 + 2 πn, n∈Z.
Ответ: x= π/6 + 2 πn, n∈Z.








 Презентация на тему Опасна ли гроза
Презентация на тему Опасна ли гроза Redaktiruemy_beydzh
Redaktiruemy_beydzh Физкультура. Виды плаванья
Физкультура. Виды плаванья О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС
О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС Письмо пером - за и против
Письмо пером - за и против Tin cup design
Tin cup design Транспорт. Виды транспорта
Транспорт. Виды транспорта Новый стандарт: обучаем и учимся
Новый стандарт: обучаем и учимся Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации
Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации Виды рабочей одежды
Виды рабочей одежды Я люблю тебя, Сакский район!
Я люблю тебя, Сакский район! Что такое значение?От П.Грайса к теории игр.
Что такое значение?От П.Грайса к теории игр. Тема лекции:«Прикладная информатика в табличном процессоре»
Тема лекции:«Прикладная информатика в табличном процессоре»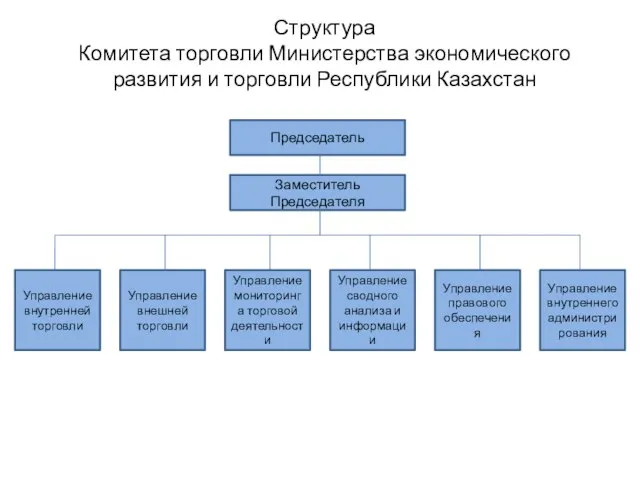 Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан
Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан Презентация на тему Информация в природе, обществе и технике
Презентация на тему Информация в природе, обществе и технике Основы коммуникативной компетентности педагогов
Основы коммуникативной компетентности педагогов Хочу отдыхать
Хочу отдыхать Урок по рассказам И.А. Бунина о любви
Урок по рассказам И.А. Бунина о любви Русская изба – поэтапное рисование
Русская изба – поэтапное рисование Известные люди Австрии
Известные люди Австрии 3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012
3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012 Викторина по произведениям А.П.Чехова « Смешные рассказы»
Викторина по произведениям А.П.Чехова « Смешные рассказы» Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г.
Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г. ЮТА (2)
ЮТА (2) Многообразие компьютеров
Многообразие компьютеров Похищение человека
Похищение человека Понятие и особенности административно правовой нормы
Понятие и особенности административно правовой нормы Техника мраморирования в современном дизайне
Техника мраморирования в современном дизайне