02-02

Пi
Пj
Xi,j
Aj
Ai
Вj
B
Bi
A
//
//
ϕι
Натуральная величина отрезка прямой
Способ прямоугольного треугольника
Дано:
[АВ] ; [АiBi]; [AjBj]
Теорема:
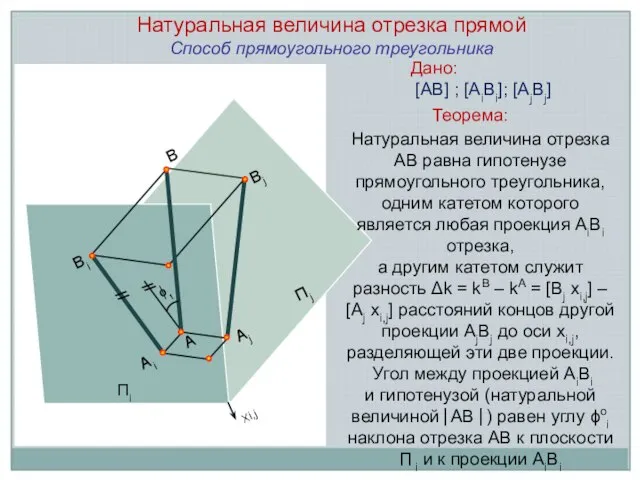
Натуральная величина отрезка АВ равна гипотенузе прямоугольного треугольника, одним катетом которого является любая проекция АiВi отрезка,
а другим катетом служит разность Δk = kB – kA = [Вj хi,j] – [Aj xi,j] расстояний концов другой проекции AjВj до оси хi,j, разделяющей эти две проекции.
Угол между проекцией АiВi
и гипотенузой (натуральной величиной ⎜АВ ⎜) равен углу ϕоi наклона отрезка АВ к плоскости П i и к проекции АiВi

Пi
Пj
Xi,j
Aj
Ai
Вj
B
Bi
A
BI
BIj
kB
kA
kAB
kAB
///
///
//
//
// //
// //
///
///
z
z
ϕι
C Ci
ппп
kA
kA
пAiBiп
kA
Доказательство:
АВI ll AiBi; BBI ⊥АВI
[АВ] – натуральная величина (гипотенуза)
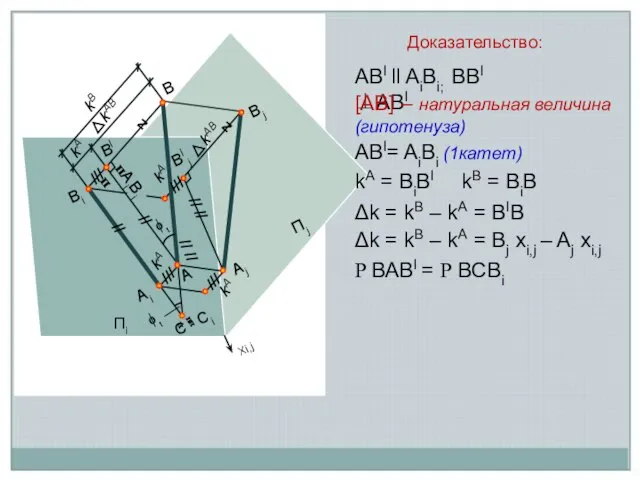
АВI= AiBi (1катет)
Δk = kB – kA = Вj хi,j – Aj хi,j
kA = ВiВI
kB = ВiВ
Δk = kB – kA = ВIВ
Р ВАВI = Р ВСBi
ϕι