Содержание
- 2. Источники Аляев Ю. А., Тюрин С. Ф. Дискретная математика и математическая логика. Андерсон Дж. Дискретная математика
- 3. Множество
- 4. Условные обозначения
- 5. Способы задания множества
- 6. Круги Эйлера 1 2 4 5 6 7 3 8
- 7. Подмножество
- 8. Собственное подмножество
- 9. Задачи
- 10. Равенство множеств
- 11. Задачи
- 14. Мощность (конечного) множества
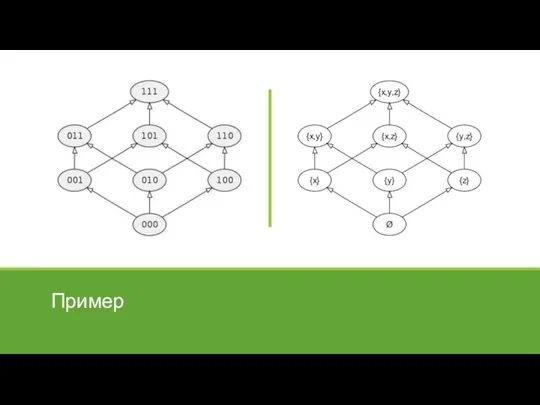
- 15. Булеан множества
- 17. Действия над множествами
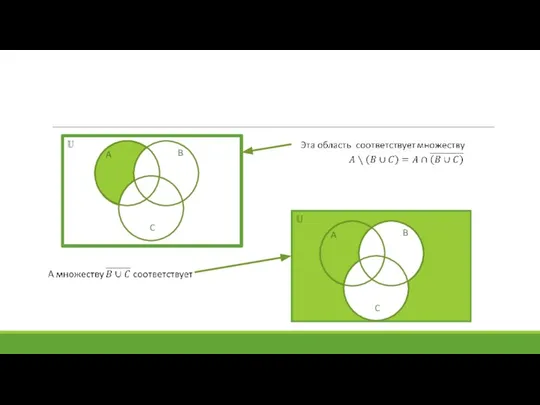
- 18. Диаграммы Венна (Эйлера-Венна) A B C D 1 2 4 5 6 7 3 8
- 19. Дополнение множества A
- 20. Дополнение множества A B
- 21. Пересечение множеств A B
- 22. Объединение множеств A B
- 23. Разность множеств A B
- 24. Симметрическая разность множеств A B
- 26. Выполняемые тождества
- 27. Кортеж
- 28. Декартово произведение множеств
- 29. Степень множества
- 30. Пример
- 31. Изображение декартова произведения
- 32. Свойства относительно операций над множествами
- 33. Комбинаторика
- 34. Источники Андерсон Дж. Дискретная математика и комбинаторика. Виленкин Н. Я., Виленкин А. Н., Виленкин П. А.
- 35. Дерево (граф) возможных вариантов Пример: Сколько трехзначных чисел можно составить из цифр 1, 3, 5 и
- 36. Правила суммы и произведения
- 37. Правило суммы
- 38. Задача В группе 24 человека. Из них 15 человек изучают английский язык, 12 – немецкий язык,
- 39. Правило произведения
- 40. Выборка
- 41. Число перестановок
- 42. Число размещений
- 43. Число сочетаний
- 44. Свойства сочетаний
- 45. Треугольник Паскаля
- 47. Отношения
- 48. Отношение
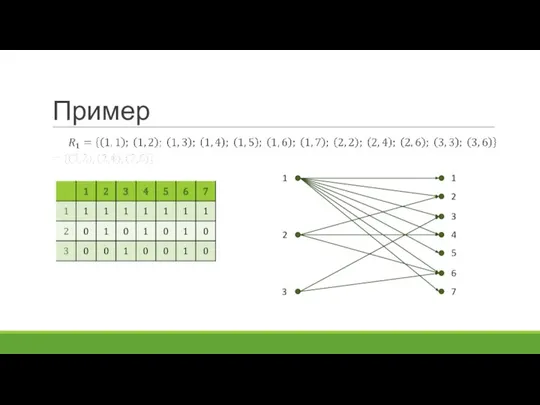
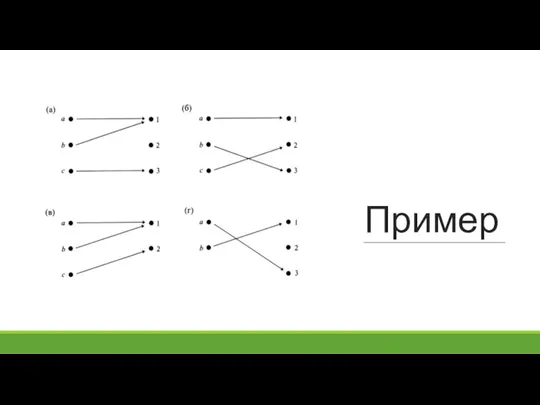
- 49. Пример
- 50. Пример 1 3 2 3 2 1 4 5 6 7
- 51. Обратное отношение
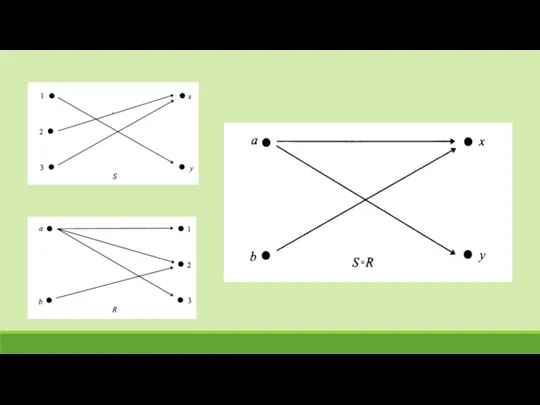
- 52. Композиция отношений
- 54. Бинарное отношение и его свойства
- 55. Виды отношений
- 56. Пример
- 57. Разбиение множества
- 58. Фактор-множество
- 60. Отображения (функции)
- 61. Отображение (функция)
- 62. Инъекция, сюръекция, биекция
- 63. Пример
- 64. Обратная функция
- 65. Композиция функций
- 66. Бесконечные множества
- 67. Конечные и бесконечные множества КОНЕЧНОЕ МНОЖЕСТВО БЕСКОНЕЧНОЕ МНОЖЕСТВО Множество, не являющееся конечным. Множество, мощность которого не
- 68. Равномощность множеств
- 69. Бесконечные множества СЧЁТНОЕ МНОЖЕСТВО Бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Множество, для которого можно
- 70. Мощность множества Класс эквивалентности по отношению равномощности.
- 71. Специальные функции
- 72. Бинарная операция
- 73. Универсальная алгебра
- 74. Полугруппа
- 75. Группа
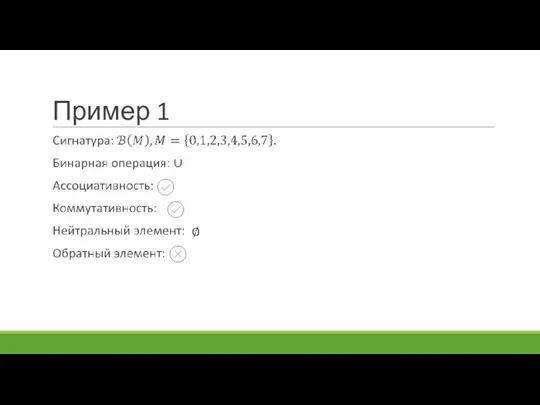
- 76. Пример 1
- 77. Пример 2
- 78. Пример 3
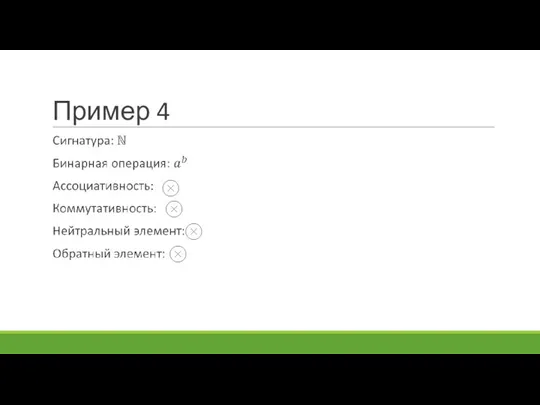
- 79. Пример 4
- 80. Пример 5
- 81. Операции коммутативной группы АДДИТИВНАЯ МУЛЬТИПЛИКАТИВНАЯ Обозначение операции: Нейтральный элемент: Противоположный элемент:
- 82. Кольцо
- 83. Пример 1
- 84. Поле Если кольцо имеет мультипликативный нейтральный элемент (единицу), оно называется кольцом с единицей. Если операция умножения
- 85. Примеры
- 87. Скачать презентацию













































































 Внешняя политика России 2 -й половины
Внешняя политика России 2 -й половины 1-е послание ап. Павла к Коринфянам гл. 15, ст. 12-19 (Зач. 159)
1-е послание ап. Павла к Коринфянам гл. 15, ст. 12-19 (Зач. 159) Хуран кукли
Хуран кукли Сейсмика на Венере.(для справки)
Сейсмика на Венере.(для справки) Старославянизмы в современном русском языке
Старославянизмы в современном русском языке «Современный сайт, как способ коммуникации между органами государственной власти и населением: тенденции, технологии, требования
«Современный сайт, как способ коммуникации между органами государственной власти и населением: тенденции, технологии, требования Реализм XIX век
Реализм XIX век Lecture Туб бренд укор
Lecture Туб бренд укор Презентация на тему Описание предметов 2 класс
Презентация на тему Описание предметов 2 класс  Презентация на тему Солженицын - Жить не по лжи
Презентация на тему Солженицын - Жить не по лжи  Современные знаки различия, эмблемы и другие различительные знаки военнослужащих РФ
Современные знаки различия, эмблемы и другие различительные знаки военнослужащих РФ Презентация на тему Всестороннее развитие детей дошкольного возраста
Презентация на тему Всестороннее развитие детей дошкольного возраста Презентация по английскому Как написать свое имя и фамилию на английском языке
Презентация по английскому Как написать свое имя и фамилию на английском языке Ринок-“невидимка” – реклама в b2b пресі
Ринок-“невидимка” – реклама в b2b пресі Технологии обучения
Технологии обучения Государственная символика РФ
Государственная символика РФ Animal Quiz
Animal Quiz ПРОЕКТ 4а КЛАССА
ПРОЕКТ 4а КЛАССА Писатели и их картины к повести Гоголя Тарас Бульба
Писатели и их картины к повести Гоголя Тарас Бульба Отчетная выставка за первое полугодие по образовательной робототехнике Mindstorms
Отчетная выставка за первое полугодие по образовательной робототехнике Mindstorms Физическая культура как средство оздоровления населения
Физическая культура как средство оздоровления населения Психоэмоциональное здоровье
Психоэмоциональное здоровье День Русской Тельняшки. Игра Нас мало, но мы в тельняшках
День Русской Тельняшки. Игра Нас мало, но мы в тельняшках Формирование месторождений
Формирование месторождений  Техника запоминания иностранных слов
Техника запоминания иностранных слов Визаж. Макияж глаз
Визаж. Макияж глаз Методы автоматизации доказательства NP-полноты двумерных локально зависимых задач
Методы автоматизации доказательства NP-полноты двумерных локально зависимых задач Понятие проекта. Тема 8
Понятие проекта. Тема 8