Содержание
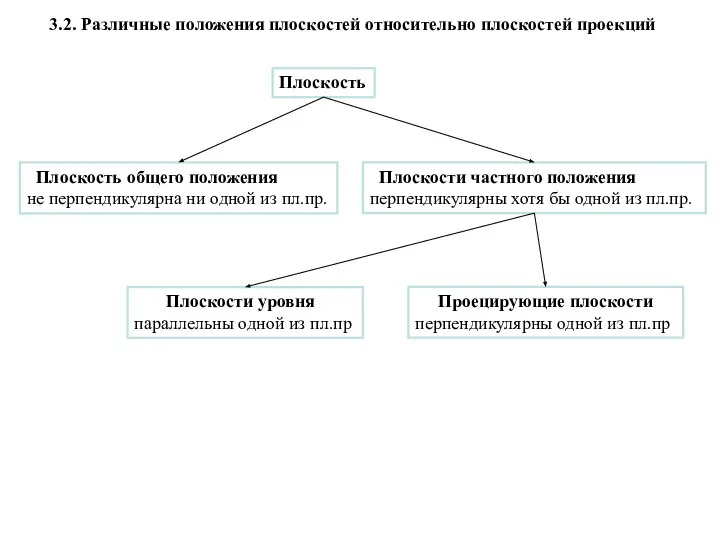
- 2. Плоскость общего положения не перпендикулярна ни одной из пл.пр. Плоскость Плоскости частного положения перпендикулярны хотя бы
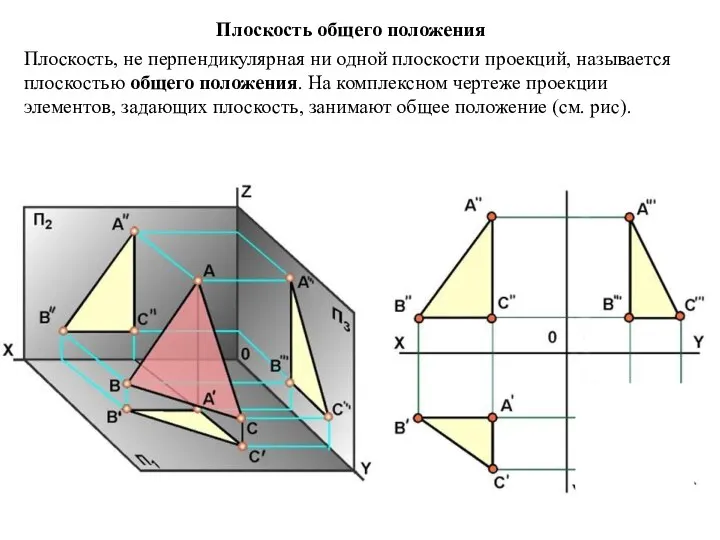
- 3. Плоскость, не перпендикулярная ни одной плоскости проекций, называется плоскостью общего положения. На комплексном чертеже проекции элементов,
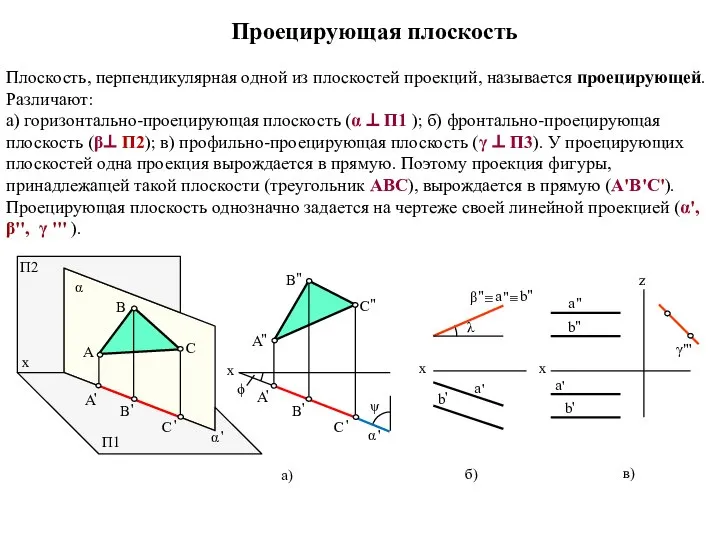
- 4. Проецирующая плоскость Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей. Различают: a) горизонтально-проецирующая плоскость (α ⊥
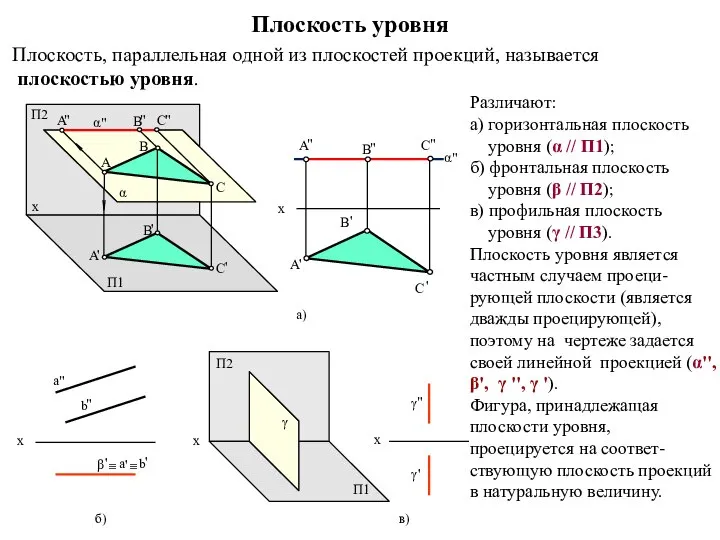
- 5. A B C П1 П2 α x x x γ x П2 П1 x а) б)
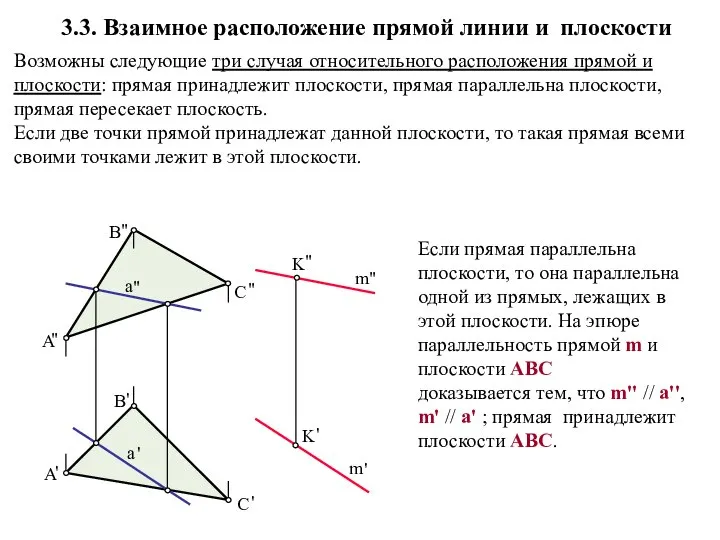
- 6. 3.3. Взаимное расположение прямой линии и плоскости Возможны следующие три случая относительного расположения прямой и плоскости:
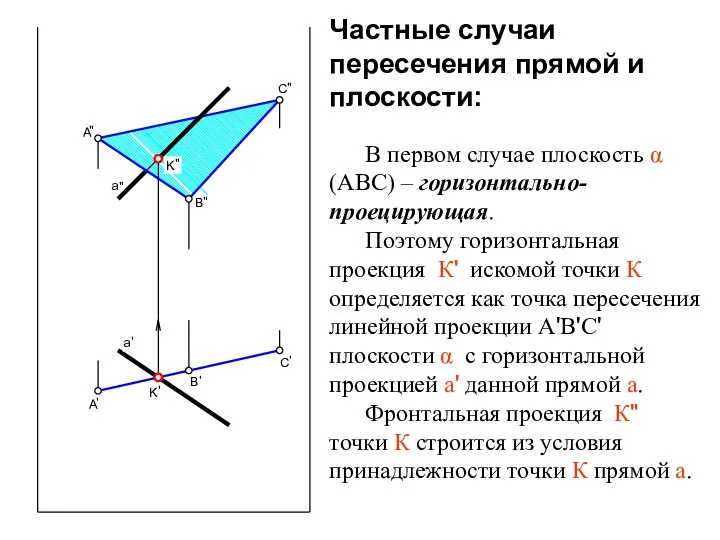
- 7. В первом случае плоскость α (АВС) – горизонтально- проецирующая. Поэтому горизонтальная проекция К' искомой точки К
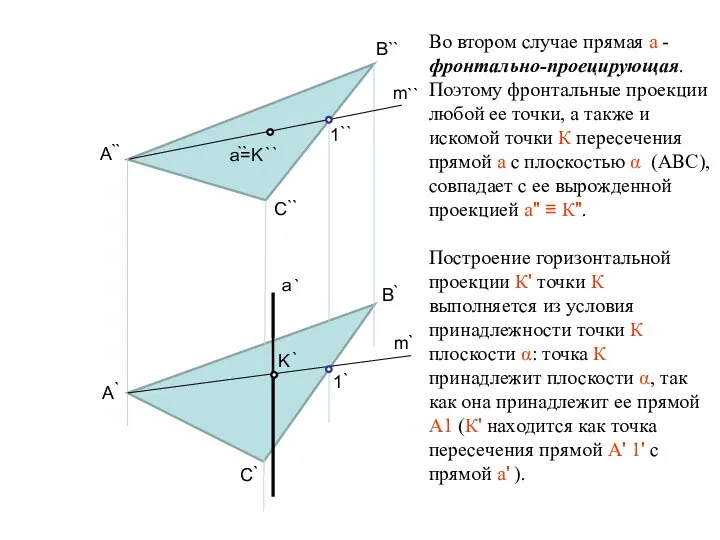
- 8. А ` ` B C А C B m m a=K K a 1 1 `
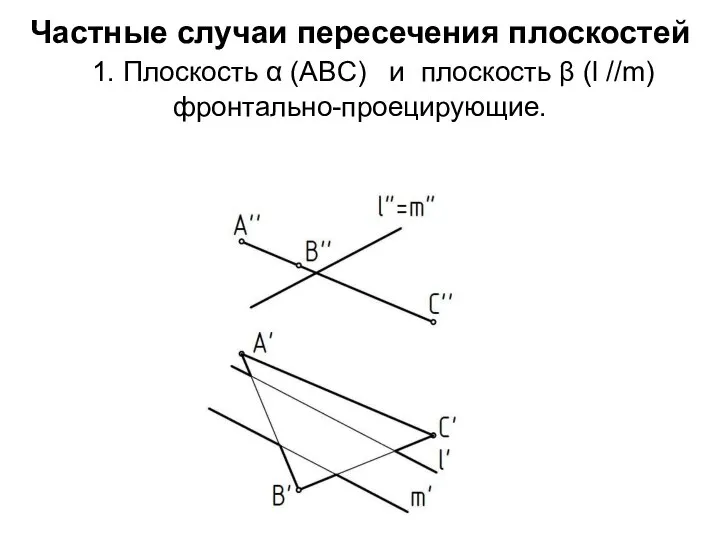
- 9. Частные случаи пересечения плоскостей 1. Плоскость α (ABC) и плоскость β (l //m) фронтально-проецирующие.
- 11. Скачать презентацию
 Путешествие в сказку
Путешествие в сказку Л.Н. Толстой как учитель: вчера, сегодня, завтра
Л.Н. Толстой как учитель: вчера, сегодня, завтра Кодирование информации в компьютере
Кодирование информации в компьютере ENGLISH FOR BEGINNERS
ENGLISH FOR BEGINNERS Пушкин - лицеист
Пушкин - лицеист Формирование ценных ориентаций личности школьника с отклонениями в поведении
Формирование ценных ориентаций личности школьника с отклонениями в поведении Модел на кариерно развитие на учителитеОсновни акценти
Модел на кариерно развитие на учителитеОсновни акценти Использование инновационных педагогических технологий в обучении и воспитании учащихся
Использование инновационных педагогических технологий в обучении и воспитании учащихся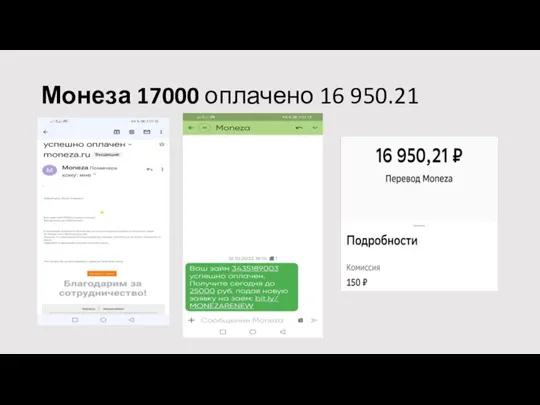 ллл
ллл VR квантум. Разработка приложений виртуальной и дополненной реальности Применение VR и AR технологий
VR квантум. Разработка приложений виртуальной и дополненной реальности Применение VR и AR технологий Грузовое устройство
Грузовое устройство Цепочки поставок фарм-продукции. Время «входа» для 3PL-оператора? 1.Основные тенденции развития Европейского и украинского фарм- рын
Цепочки поставок фарм-продукции. Время «входа» для 3PL-оператора? 1.Основные тенденции развития Европейского и украинского фарм- рын ДискретизацияСверткаДПФ
ДискретизацияСверткаДПФ Сетевой этикет при дистанционном обучении Никуличева Наталия Викторовна зав.кафедрой дистанционного обучения ФИРО
Сетевой этикет при дистанционном обучении Никуличева Наталия Викторовна зав.кафедрой дистанционного обучения ФИРО Заключительный урок по теме «Жизнь и творчество Владимира Маяковского»
Заключительный урок по теме «Жизнь и творчество Владимира Маяковского» эффективный и экономичный канал привлечения клиентов Казань: 850 000 писем в неделю 240 000 подписчиков (2,38%)
эффективный и экономичный канал привлечения клиентов Казань: 850 000 писем в неделю 240 000 подписчиков (2,38%) История русской одежды
История русской одежды Использование ИКТ на уроках географии
Использование ИКТ на уроках географии Манипуляция и способы противостоять
Манипуляция и способы противостоять Здравствуйте! Event агентство Фейерверк волшебства радо предложить Вам концепцию программы, проведения Вашего праздника. Программа
Здравствуйте! Event агентство Фейерверк волшебства радо предложить Вам концепцию программы, проведения Вашего праздника. Программа  Современные модели развития науки Подготовила студентка группы Тс05/1413 Захарова Кристина Дисциплина: Концепции современного ес
Современные модели развития науки Подготовила студентка группы Тс05/1413 Захарова Кристина Дисциплина: Концепции современного ес Сетевые технологии: терминология, устройства
Сетевые технологии: терминология, устройства Презентация инновационного проекта
Презентация инновационного проекта ОПИСАНИЕ ВОЗМОЖНОСТЕЙ НОВОЙ ВЕРСИИ «СБОР РБД», ОСОБЕННОСТИ ФУНКЦИОНИРОВАНИЯ МОДЕРНИЗИРОВАННЫЙ МЕХАНИЗМ МЕЖУРОВНЕВОГО ВЗАИМОД
ОПИСАНИЕ ВОЗМОЖНОСТЕЙ НОВОЙ ВЕРСИИ «СБОР РБД», ОСОБЕННОСТИ ФУНКЦИОНИРОВАНИЯ МОДЕРНИЗИРОВАННЫЙ МЕХАНИЗМ МЕЖУРОВНЕВОГО ВЗАИМОД Магистерская диссертация. Двухсекторная модель экономики с неоднородным трудом.
Магистерская диссертация. Двухсекторная модель экономики с неоднородным трудом. Всероссийская акция. Шаблон
Всероссийская акция. Шаблон Презентация на тему Тэффи "Жизнь и воротник"
Презентация на тему Тэффи "Жизнь и воротник" Кружок «КРАЕВЕДЫ»
Кружок «КРАЕВЕДЫ»