1.Обратные тригонометрические функции.

Вычислите:
Решение. Если использовать понятия косинуса и котангенса острого угла прямоугольного треугольника, теорему Пифагора и свойство
биссектрисы треугольника, то задача решается почти мгновенно.
На рис. 3 изображен треугольник АВС,
, в котором
ACB = 90°,
ВС = 5, АВ = 13
и ВМ - биссектриса
угла АВС. Следовательно,
МС = 5х,
АМ= 13х и АС= 12,
отсюда
. Тогда
Вычислите
Решение.
Рассмотрим равнобедренный треугольник АBС,
где АB=BС=41, ВМ
АС,
ВМ=40,CN
AB
(рис.4). Отрезок AM согласно
теореме
Пифагора имеет длину, равную 9.
Видно, что
Воспользовавшись подобием прямоугольных треугольников ANC и AMB, найдем
ЗАДАЧА 3.
ЗАДАЧА 4.

2. Алгебраические выражения.
Часто в алгебре встречаются задания, в которых по заданным условиям на переменные, необходимо найти значение некоторого выражения, содержащего их.
ЗАДАЧА 5.
Из условий
,
и
для положительных х, у и z, не вычисляя
их значений, указать значение
выражения
Решение. Привычное задание решить систему уравнений
у учащихся затруднений не вызывает.
Однако в данном случае
нужно,
не решая систему, ответить на вопрос, чему равно значение выражения ху + yz.
По теореме, обратной теореме Пифагора,
числа х, у и z являются соответственно длинами катетов и гипотенузы треугольника ABD с прямым углом D. А, рассмотрев второе
уравнение системы, можно сделать вывод, что у, z и 4 также есть соответственно длины катетов и гипотенузы треугольника BCD
с прямым углом D (рис. 6).
Третье уравнение системы разрешает утверждать,
что число у есть среднее пропорциональное
чисел х и z, и по теореме,
обратной
теореме о пропорциональных отрезках в прямоугольном треугольнике, угол АВС — прямой.
Теперь рассмотрим выражение ху + yz.
Примечание. Для данной системы уравнений задания могут быть и другие. Например, найти
значение выражения х + у + z или
в каком отношении находятся числа х и у; z и у; х + z и у.
Ответ: 12

.
Для положительных х, у и z из условий
не находя значения х, у и z,
вычислите значение выражения ху + уz + zx.
Решение.
Запишем три условия задачи в виде системы уравнений
По теореме, обратной теореме, Пифагора, числа
и 5 являются длинами соответственно
катетов и гипотенузы
треугольника АОС с прямым углом АОС.
Числа х,
Задача 6.
и 13 есть длины сторон треугольника АОВ с углом АОВ, равным 135°. Этот вывод можно сделать, используя
теорему, обратную теореме косинусов. Аналогично, x,
и 12 есть длины сторон треугольника ВОС с углом ВОС, равным 135°.
На рис. 8 изображены эти треугольники.
Поскольку 52 + 122 = 132, то в треугольнике АВС
ACB = 90°. Теперь найдем площади
треугольников АОВ, АОС, ВОС, АВС.
Видно, что значение выражения ху + yz +zx равно учетверенной площади треугольника ABC.
Итак, xy+yz+zx =120
Ответ:120

ЗАДАЧА 7.
Для положительных х, у и z, не вычисляя их значения из системы уравнений
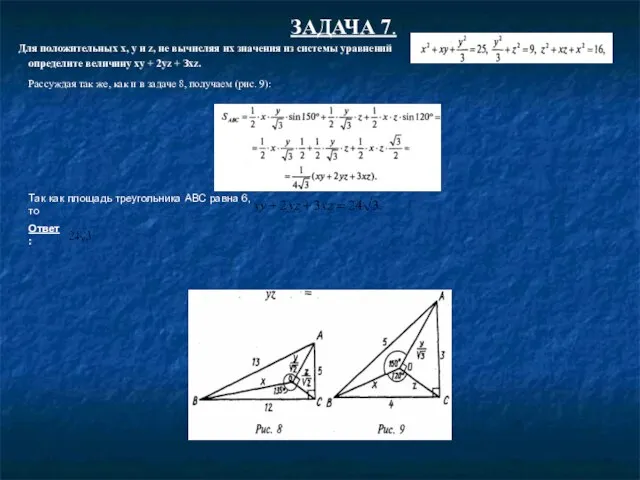
определите величину ху + 2уz + Зxz.
Рассуждая так же, как и в задаче 8, получаем (рис. 9):
Так как площадь треугольника AВС равна 6, то
Ответ:

3. Системы уравнений.
Решению систем уравнений в алгебре отводится достаточно большое внимание. Они встречаются и в
Поэтому, тем более, интересен такой нестандартный подход к решению некоторых систем
уравнений, рассмотренных в этом пункте.
ЗАДАЧА 8.
Имеет ли система уравнений
решения для х > 0, у > 0 и z> 0?
рис.10
Допустим, что есть такая тройка положительных чисел х, у и z, удовлетворяющая каждому уравнению данной системы.
Тогда возможна ее геометрическая интерпретация, как в задаче 8 (рис.10).
Но такого треугольника АВС не может быть, так как не выполняется неравенство
треугольника. Значит, система не имеет решений.
Примечание. Для положительных x,y и z данная система имеет решение, если в правой части третьего уравнения поставить число
из промежутка (1; 25).
Ответ: нет решений.
вариантах ЕГЭ.

то
Решите систему уравнений
Решение. Нетрудно убедиться, что х и у положительны. Поскольку
числа у,
и х являются длинами
соответственно катетов и гипотенузы треугольника
АВС с прямым углом АСВ (рис. 11).
Площадь этого треугольника 24 кв. ед., а его периметр 24 ед. Поэтому радиус окружности, вписанной в треугольник АВС, равен 2.
Так как длина гипотенузы АВ равна сумме длин катетов АС и ВС без удвоенной длины радиуса вписанной в треугольник окружности,
то
Из второго уравнения системы получаем х = 10. Значит, у = 6 или у = 8.
Ответ: (10; 6), (10; 8).
ЗАДАЧА 9.

ЗАДАЧА 10.
Решите систему уравнений
Решение.
Первое уравнение системы задает плоскость, второе — сферу. Если их изобразить, то
очевидно, что 0<х<1, 0 < у < 1, 0
Согласно первому уравнению
Тогда второе уравнение принимает вид
(*)
Преобразовав его, получаем квадратное уравнение относительно х:
Дискриминант этого уравнения равен - (у
-1)2.
Следовательно, -(у
-1)2
0. Это
неравенство выполняется при
Уравнение (*) можно было преобразовать в квадратное относительно у с решением
Значение
находится из первого уравнения.
Примечание. Задачу можно переформулировать, например, так: «Определите вид треугольника, периметр которого равен
а сумма квадратов длин его сторон равна 1».
,

ЗАДАЧА 11.
Решите систему уравнений
Решение.
Уравнение x+y+z=3 - есть уравнение плоскости (рис. 12), пересекающей оси прямоугольной
декартовой системы
координат в , А(3;0;0), B(0;3;0), С(0; 0; 3).
Уравнение
есть уравнение сферы с центром в точке O(0; 0; 0) и радиусом R,
равным
Вычислим расстояние от точки О до плоскости AВС. Для этого рассмотрим тетраэдр ОАВС.
Объем V тетраэдра равен
где H=OD (D — центр треугольника АВС).
Этот объем можно найти иначе:
Приравняв
и
, получаем H=
. Это означает, что расстояние от точки О до плоскости АВС равно радиусу сферы, а значит,
плоскость касается сферы. Следовательно, точка касания является центром треугольника АВС. Поскольку D(x; у; z) — центр
равностороннего треугольника АВС,
где А(3; 0; 0), В(0; 3; 0),
С(0;0;3), то x=y=z.
Заменив у и z на х в уравнениях данной системы, получаем x=1.
Ответ: (1; 1; 1).

ЗАДАЧА 12.
Решите систему уравнений
Решение.
Рассмотрим слагаемые левой части второго уравнения:
Пусть это расстояние между точками М(х; у) и A(2;-1).
Допустим, что это расстояние между точками М (х;у} и В(10; 5).
Найдем расстояние между точками А(2; -1) и В(10;5):
Итак, второе уравнение системы можно интер­претировать как равенство AM + ВМ = АВ. Это дает нам право утверждать, что
точка М принадлежит отрезку АВ, т.е. 2 ≤ х ≤ 10 и -1 ≤ у ≤ 5
Составим уравнение прямой АВ, проходящей через точки А(2; -1) и B(10; 5).
и
Отсюда
т.е.
, или Зх — 4у = 10.
Запишем новую систему:
Значит, х = 6 и у = 2.
Ответ: (6; 2).

4. Аналитический способ решения.
Рассмотрим аналитический способ решения некоторых задач, рассмотренных выше, чтобы была возможность
убедиться в том, что геометрический подход дает более быстрое, а главное, красивое решение этих задач.
ЗАДАЧА 1.
Рассмотрим аналитический способ решения.
Решение.
Обозначим:
где
Найдем
Таким образом,
учитывая условие, что
получим, что k=1 и
т.е.
Ответ:
ЗАДАЧА 2.
Решим систему аналитически:
Решение:
Обозначим уравнение
- (1),