2 закон композиции. Закон пропорций. Пропорции в костюме

Закон пропорций определяет отношение частей целого друг к другу и к целому.
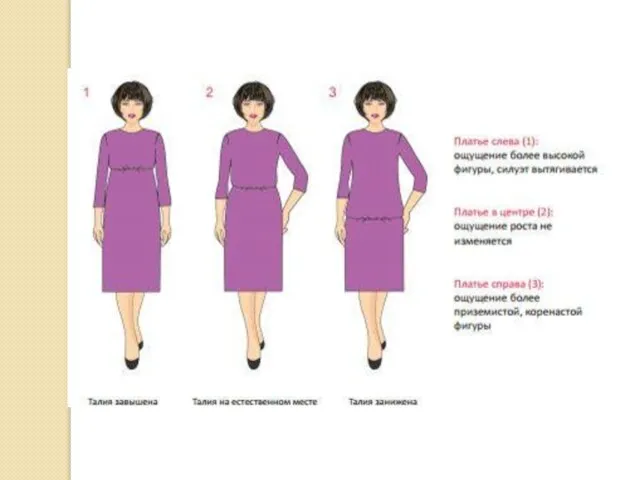
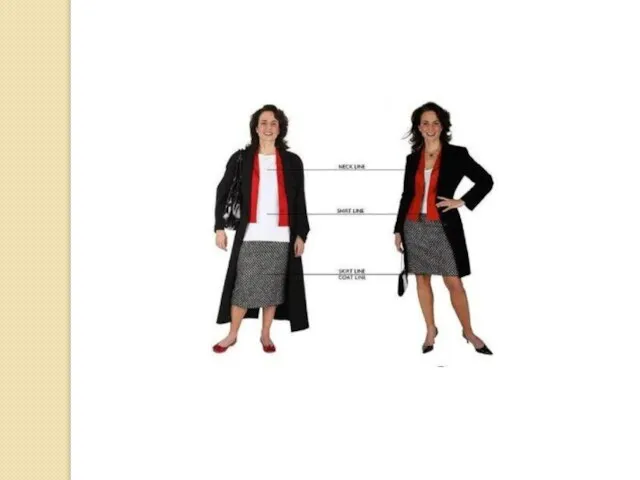
Части, элементы художественного целого, связанные между собой пропорциональными отношениями, единым модулем или масштабом приобретают соразмерность и тем самым гармонизуют форму.

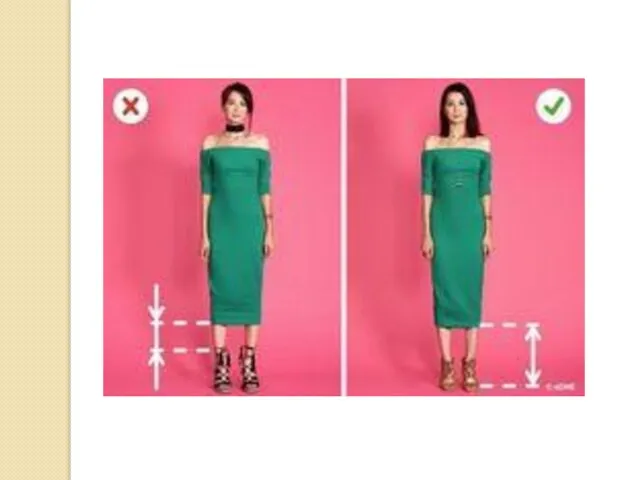
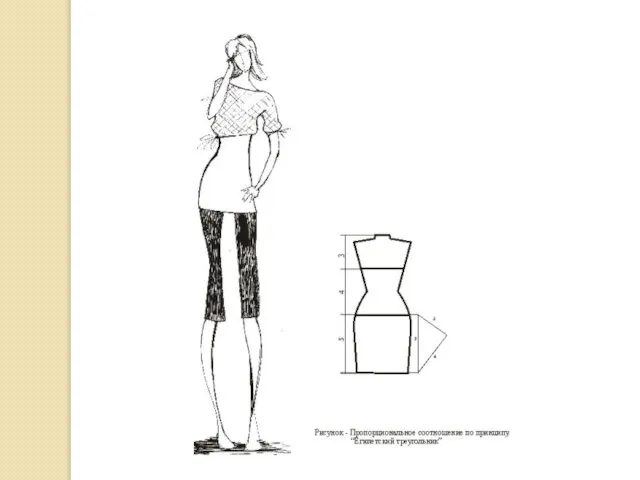
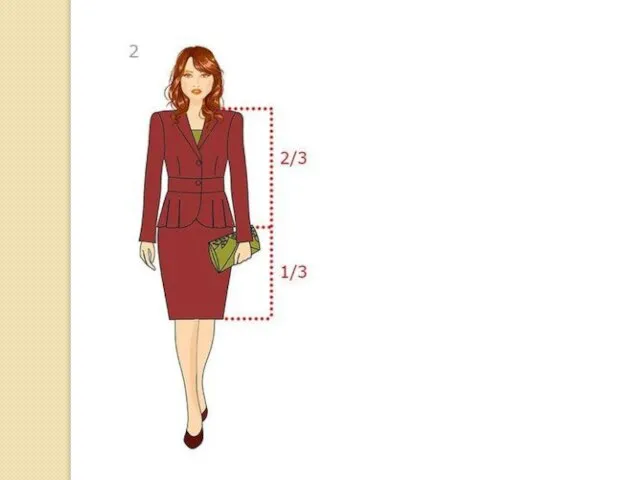
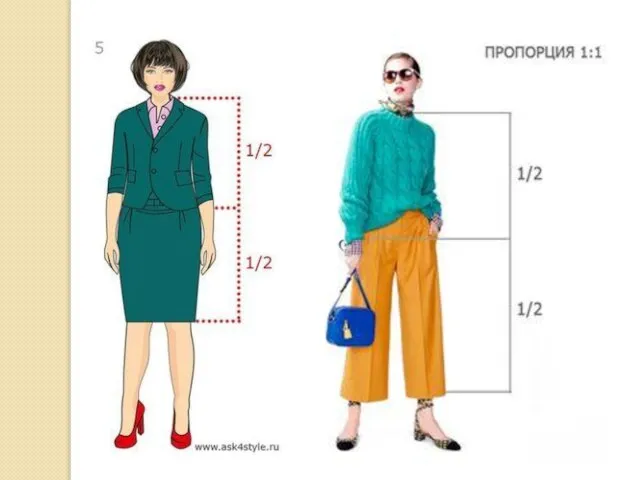
Простые пропорциональные отношения
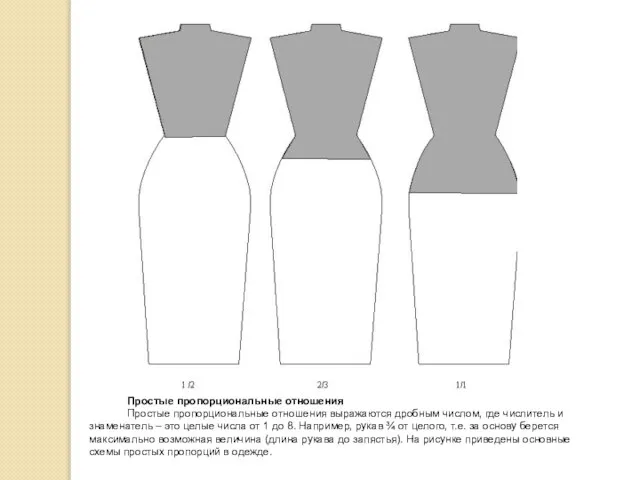
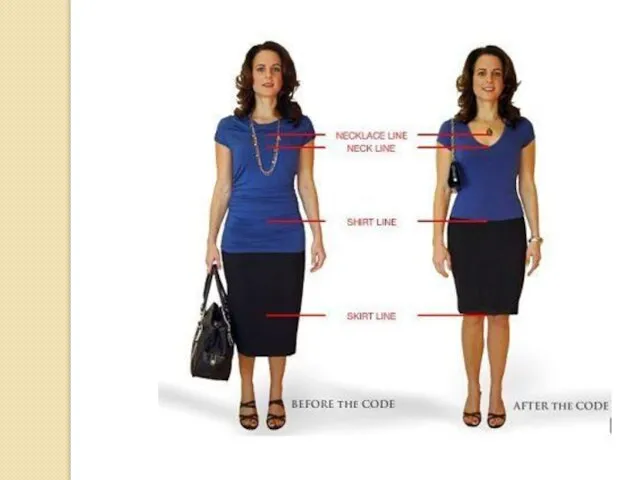
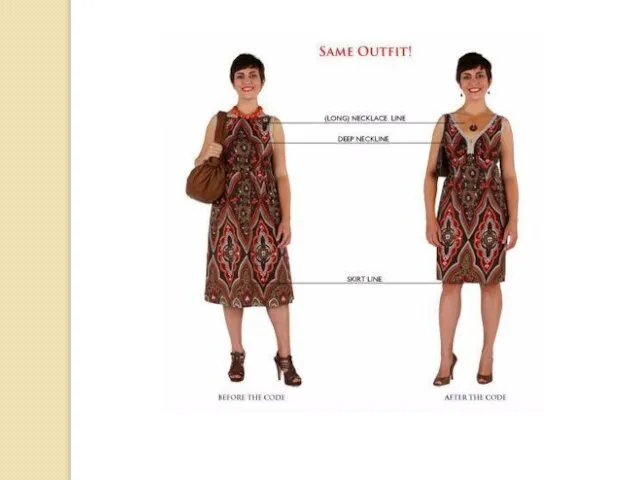
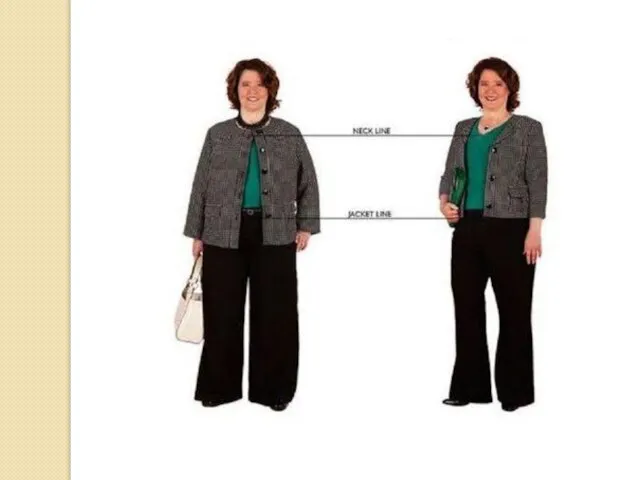
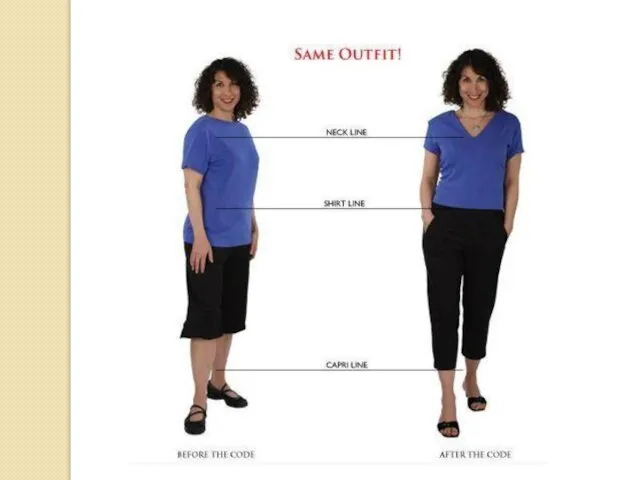
Простые пропорциональные отношения выражаются дробным числом, где числитель и знаменатель – это целые числа от 1 до 8. Например, рукав ¾ от целого, т.е. за основу берется максимально возможная величина (длина рукава до запястья). На рисунке приведены основные схемы простых пропорций в одежде.

Сложные пропорциональные отношения
Начиная с древности, с поисков наиболее гармоничных пропорций, были найдены сложные пропорции, основанные на иррациональных числах, которые выводились с помощью математических решений и геометрических построений.
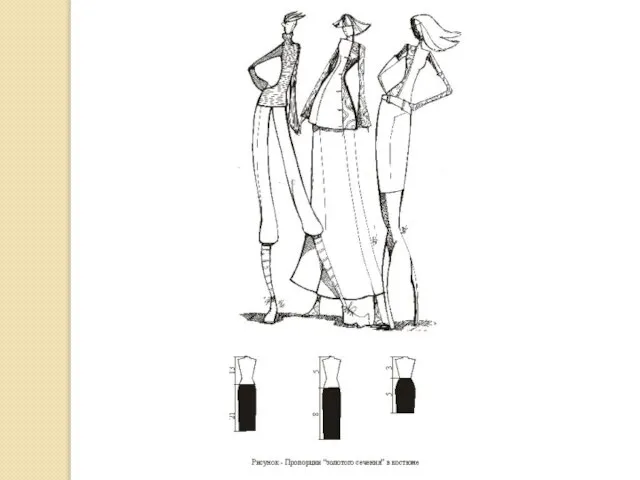
Разновидностью сложной пропорции является пропорция так называемого «золотого сечения», имеющая всего два члена – «а» и «в» - излюбленная пропорция художников, которую в эпоху Возрождения называли «божественной пропорцией».
«Золотое сечение» является самой гармоничной пропорцией.
Пропорция считается «золотым сечением» тогда, когда меньшая часть относится к большей так как большая часть относится к целому. При делении отрезка, согласно «золотому сечению», сторона АВ будет относиться к стороне ВС так, как ВС – к АС. Особенностью пропорции «золотого сечения» является то, что в ней последний член представляет собой разность между двумя предыдущими членами, т.е., а:в=в:(а -в).