Содержание
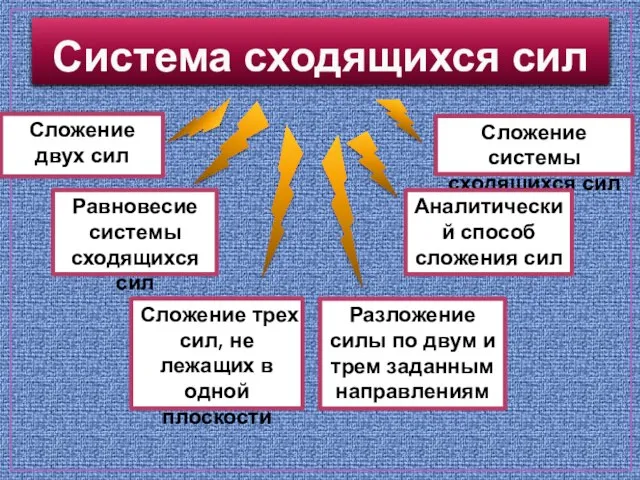
- 2. Система сходящихся сил Сложение двух сил Сложение трех сил, не лежащих в одной плоскости Сложение системы
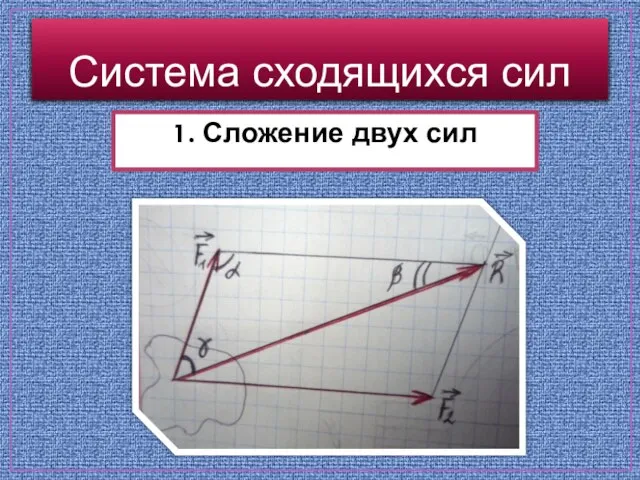
- 3. 1. Сложение двух сил Система сходящихся сил Геометрическая сумма R двух сил F1 и F2 находится
- 4. Система сходящихся сил 1. Сложение двух сил
- 5. 2. Сложение трех сил, не лежащих в одной плоскости Система сходящихся сил
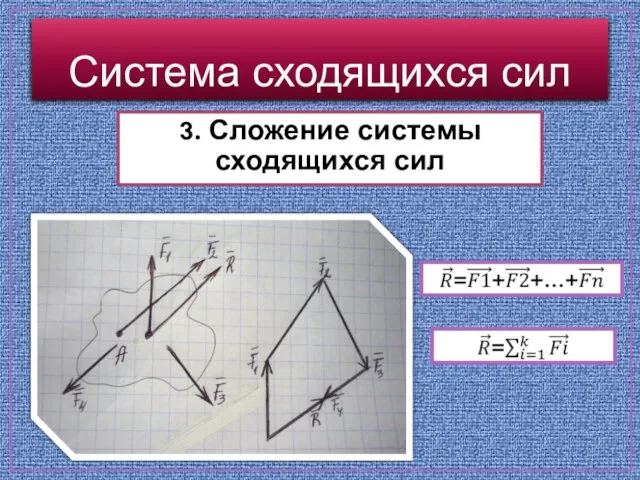
- 6. 3. Сложение системы сходящихся сил Система сходящихся сил Рассмотрим систему сходящихся сил, т.е. линии действия пересекаются
- 7. Система сходящихся сил 3. Сложение системы сходящихся сил
- 8. Система сходящихся сил 4. Разложение силы по двум и трем заданным направлениям Разложить данную силу на
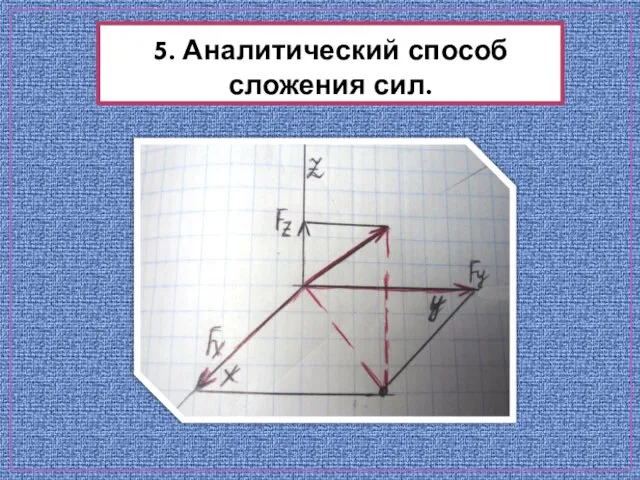
- 9. 5. Аналитический способ сложения сил. Система сходящихся сил Этот метод основывается на понятии о проекции силы
- 10. 5. Аналитический способ сложения сил.
- 11. 6. Равновесие системы сходящихся сил Система сходящихся сил Для равновесия системы сходящихся сил, приложенных к твердому
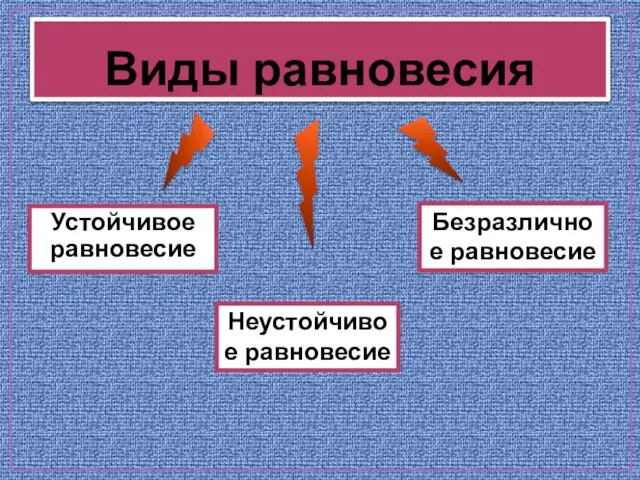
- 12. Виды равновесия Устойчивое равновесие Неустойчивое равновесие Безразличное равновесие
- 13. Равновесие называется устойчивым, если возникшая сила стремится вернуть тело в положение равновесия. Виды равновесия Равновесие называется
- 14. Вывод о видах равновесия: 1. Устойчиво то положение тела, в котором его потенциальная энергия имеет минимальное
- 16. Скачать презентацию








 Что такое письмо?
Что такое письмо? The philosophy of the Modern Ages
The philosophy of the Modern Ages Исследовательский проект«Река Ихаланийоки»
Исследовательский проект«Река Ихаланийоки» Экипаж - воздушное судно как полиэргатическая сложная система. Тема 6
Экипаж - воздушное судно как полиэргатическая сложная система. Тема 6 Презентация на тему Концепция ноосферы Вернадского В.И.
Презентация на тему Концепция ноосферы Вернадского В.И. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ГРУНТАХ
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ГРУНТАХ Обучение детейс разным типом мышления
Обучение детейс разным типом мышления Золотая осень
Золотая осень Автор: Попова Л.Б. учитель музыки Подоскляйского филиала им. Героя Советского Союза А.Н. Московского МОУ Нижнеспасской СОШ
Автор: Попова Л.Б. учитель музыки Подоскляйского филиала им. Героя Советского Союза А.Н. Московского МОУ Нижнеспасской СОШ Перронные автобусы
Перронные автобусы  Презентация на тему К.И. Чуковский Путаница литературное чтение 2 класс
Презентация на тему К.И. Чуковский Путаница литературное чтение 2 класс Презентация на тему ЛУЧ
Презентация на тему ЛУЧ  Детский рисунок. Психологическая польза рисования
Детский рисунок. Психологическая польза рисования EggDefend. Оценка эффективности групповой работы
EggDefend. Оценка эффективности групповой работы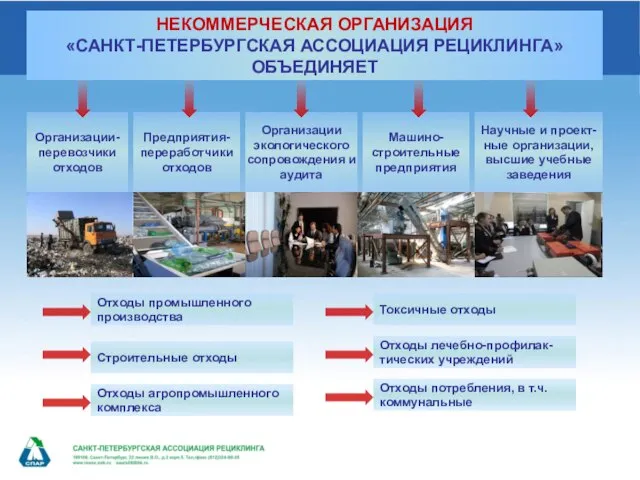 НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ«САНКТ-ПЕТЕРБУРГСКАЯ АССОЦИАЦИЯ РЕЦИКЛИНГА» ОБЪЕДИНЯЕТ
НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ«САНКТ-ПЕТЕРБУРГСКАЯ АССОЦИАЦИЯ РЕЦИКЛИНГА» ОБЪЕДИНЯЕТ Внутренняя политика Екатерины II (7 класс)
Внутренняя политика Екатерины II (7 класс) Преступления против жизни и здоровья
Преступления против жизни и здоровья Презентация на тему Жирафы
Презентация на тему Жирафы Визуал
Визуал Будни и праздники начальной школы
Будни и праздники начальной школы Проект реализуется в рамках программы «Муниципальный менеджер 2.0» управления по делам молодежи Новосибирской области
Проект реализуется в рамках программы «Муниципальный менеджер 2.0» управления по делам молодежи Новосибирской области Взаимодействие буддийской и синтоистской традиций на примере культа Тэндзин
Взаимодействие буддийской и синтоистской традиций на примере культа Тэндзин Как зарегистрировать ученика в Ekool ?
Как зарегистрировать ученика в Ekool ? Шинная фантазия
Шинная фантазия Презентация на тему Музыкальные шедевры П.И. Чайковского на уроках литературы
Презентация на тему Музыкальные шедевры П.И. Чайковского на уроках литературы  Так ли важен завтрак?
Так ли важен завтрак? Конфликтология в социальной работе
Конфликтология в социальной работе Республика Хакасия
Республика Хакасия