9 класс.

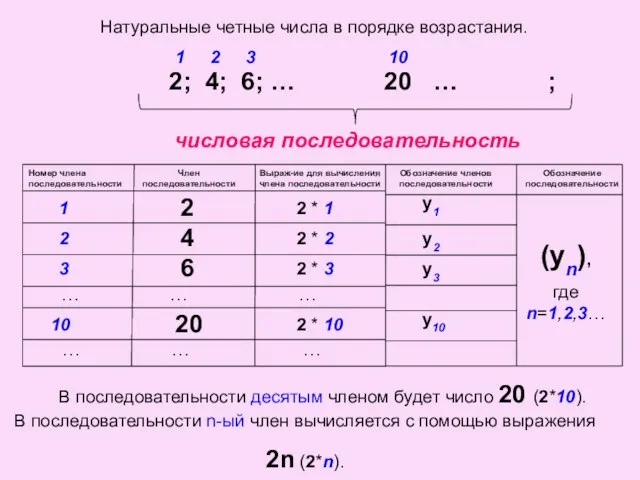
Натуральные четные числа в порядке возрастания.
2; 4; 6; … … ;
числовая последовательность
В данной последовательности число 2 стоит на первом месте.
1
Число 4 стоит на втором месте.
2
Число 6 стоит на третьем месте.
3
10
20
В последовательности n-ый член вычисляется с помощью выражения
2n (2*n).
Номер члена последовательности
Член последовательности
Выраж-ие для вычисления члена последовательности
2 * 1
2 * 2
2 * 3
10
2 * 10
20
Обозначение членов последовательности
y1
y2
y3
y10
Обозначение последовательности
(yn),
где n=1,2,3…
В последовательности десятым членом будет число 20 (2*10).

Правильные дроби с числителем, равным 1 в порядке убывания.
числовая последовательность
1
2
3
…
n

y = f (x)
Множество значений функции натурального аргумента называют числовой последовательностью.
f(1)=y1 ; f(2)=y2 ; f(3)=y3 ; ….. f(n)=yn ….. .
y1 ; y2 ; y3 ; ….. yn ; …. .
числовая последовательность
(yn) – обозначение числовой последовательности.
y1 , y2 , y3 , ….. yn – члены числовой последовательности.

Последовательность натуральных чисел, которые при делении на 4 дают в остатке 1.
1 ; 5 ; 9 ; 13 ; 17 ; 21 ; … .
1
а1 = 1
5
а2 = 5 = 1 + 4
1
1
а1
9
а3 = 9 = 5 + 4
5
5
а2
а4 = 13 = 9 + 4
13
9
9
а3
…
называется арифметической прогрессией(аn).
Арифметическая прогрессия.
an = an-1 + 4
a2k+3 = a2k+2 + 4
а1- предыдущий для а2
а2- предыдущий для а3
а3- предыдущий для а4
Последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом,

Последовательность (an) - арифметическая прогрессия,
если для любого натурального n выполняется условие
an+1=an+d, где d некоторое заданное число (разность арифметической прогрессии ).
Последующий член арифметической прогрессии равен предыдущему члену сложенному с разностью.
d=an+1- an

a2n+3
7
a2n+3=7.
2n+3
(an)
- обозначение арифметической прогрессии;
-обозначение члена арифметической прогрессии;
- номер члена арифметической прогрессии;
- значение a2n+3 члена арифметической прогрессии.
Элементы записи члена арифметической прогрессии

Геометрическая прогрессия.
Последовательность, членами которой являются степени числа 2 с натуральным показателем.
2 ; 4 ; 8 ; 16 ; 32 ; 64 ; … .
а1 = 2
2
4
а2 = 4 = 2 * 2
2
2
а1
8
а3 = 8 = 4 * 2
4
4
а2
а4 = 16 = 8 * 2
16
8
8
а3
…
называется геометрической прогрессией(bn).
а1-предыдущий для а2
а2-предыдущий для а3
а3-предыдущий для а4
an = an-1 * 2
a2k+3 = a2k+2 * 2
Последовательность, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число,

Последовательность (bn) - геометрическая прогрессия,
если для любого натурального n выполняются условия
bn≠0 и bn+1=bn*q, где q - заданное некоторое число(знаменатель геометрической прогрессии).
Последующий член геометрической прогрессии равен предыдущему члену, умноженному на знаменатель.