Алгебра Логики

История предмета
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

История алгебры логики
Понятие логики как науки появилось ещё в XIX в., т.е. задолго до появления науки информатики и компьютеров. Элементы математической логики можно найти уже в работах древнегреческих философов. В XVII в. Г. В. Лейбниц высказал идею о том, что рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам. Однако как самостоятельный раздел математики логика начала формироваться только с середины XIX в..
Для того чтобы рассуждать, человеку необходим какой-либо язык. Не удивительно, что математическая логика начиналась с анализа того, как говорят и пишут люди на естественных языках. Этот анализ привёл к тому, что выяснилось существование формулировок, которые невозможно разделить на истинные и ложные, но, тем не менее, выглядят осмысленным образом. Это приводило к возникновению парадоксов, в том числе в одной из фундаментальных наук математики. Тогда было решено создать искусственные формальные языки, лишённого «вольностей» языка естественного.

НАЧАЛА
Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения "ученик десятого класса" и "информатика — интересный предмет". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие "интересный предмет". Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.

Булевы функции
Пусть имеется некоторый набор высказываний, о которых можно говорить определённо, что они истинные или ложные. Обозначим их латинскими буквами A, B, C, D … .
Если у нас есть два простых предложения, то из них образовать новое, сложносочинённое предложение с помощью союзов «или» либо «и». В математической логике для этой цели используются специальные символы:
знак дизъюнкции v
знак конъюнкции & (иногда используется ^)
Знак NOT – знак отрицания

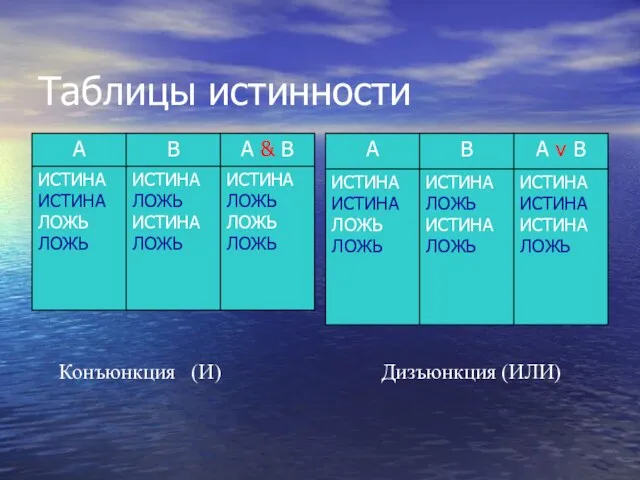
Утверждение A v B считается истинным тогда и только тогда, когда истинно хотя бы одно из исходных утверждений;
утверждение A & B – когда истинны оба утверждения.

Таблицы истинности
Конъюнкция (И) Дизъюнкция (ИЛИ)

Преобразование выражений, состоящих из булевых функций.
В математической логике преобразование выше указанных выражений проводится для различных целей – от упрощения исходного до доказательства утверждений. В информатике же оно используется в основном для упрощения, ведь при производстве цифровой электроники, как и любого другого товара, требуются наименьшие затраты. Для упрощения булевых выражений используются те же методы, что и при упрощении алгебраических. Для начала была проведена аналогия между алгебраическими операторами от двух аргументов (сложение, вычитание, умножение и т.д.) и булевыми.

Было выяснено, что умножение и логическое «И» обладают сходными свойствами
- от перестановки мест аргументов результат не изменяется
A & B = B & A
- существует следующий закон A & (B & C) = (A & B) & C

Существуют некоторые тождества, опирающиеся на особые свойства функции, например:
A & (~A) = ЛОЖЬ
(~A) & (~B) = ~ (A v B)

Сложение и логическое «ИЛИ»:
- от перестановки мест аргументов результат не изменяется
A v B = B v A
- существует следующий закон
(A v B) v С = A v (B v C)
- можно выносить общий множитель за скобки
(A & B) v (С & B) = B & (A v C)

Некоторые собственные законы сложения:
A v (~A) = ИСТИНА
(~A) v (~B) = ~ (A & B)

Нахождение исходного выражения по его значениям.
В отличие от алгебраических выражений, булевы можно восстановить, зная их аргументы и соответственные им значения. Пусть нам дана булева функция от 3 переменных:
Составим для неё таблицу и условимся обозначать ИСТИНУ - 1, а ЛОЖЬ – 0.

Для начала выпишем все аргументы функции, при которых функция равна 1.
F (1, 1, 0) = 1
F (1, 0, 1) = 1
F (1, 1, 1) = 1

Теперь запишем 3 таких выражения (функция принимает значение 1 три раза), что они принимают значение 1 только при вышеуказанных значениях
X1 & X2 & (~X3)
X1 & (~X2) & X3
X1 & X2 & X3

И запишем их логическую сумму:
(X1 & X2 & (~X3)) v (X1 & (~X2) & X3) v (X1 & X2 & X3) – это выражение принимает значение 1 при тех же значениях, что и исходная функция. Полученное выражение можно упростить.

Упростим
(X1 & X2 & (~X3)) v (X1 & (~X2) & X3) v (X1 & X2 & X3) =
= X1 & ((X2 & (~X3)) v ((~X2) & X3) v (X2 & X3)) =
= X1 & ((X2 & (~X3)) v X3 & ((~X2) v X2)) =
= X1 & ((X2 & (~X3)) v X3)

Применение в вычислительной технике и информатике
После изготовления первого компьютера стало ясно, что при егопроизводстве возможно использование только цифровых технологий –ограничение сигналов связи единицей и нулём для большей надёжности ипростоты архитектуры ПК. Благодаря своей бинарной природе, математическаялогика получила широкое распространение в ВТ и информатике.

Были созданыэлектронные эквиваленты логических функций, что позволило применять методыупрощения булевых выражений к упрощению электрической схемы. Кроме того,благодаря возможности нахождения исходной функции по таблице позволилосократить время поиска необходимой логической схемы. В программировании логика незаменима как строгий язык и служит дляописания сложных утверждений, значение которых может определить компьютер.