Алгебра суждений

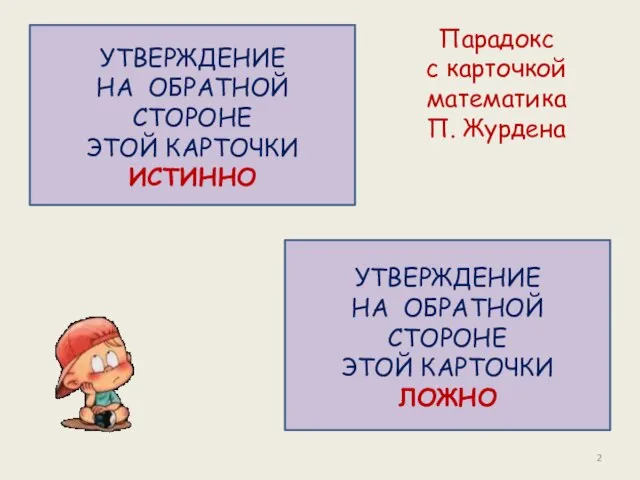
УТВЕРЖДЕНИЕ
НА ОБРАТНОЙ СТОРОНЕ
ЭТОЙ КАРТОЧКИ
ИСТИННО
УТВЕРЖДЕНИЕ
НА ОБРАТНОЙ СТОРОНЕ
ЭТОЙ КАРТОЧКИ
ЛОЖНО
Парадокс
с карточкой математика
П. Журдена

Основная задача логики высказываний заключается в том, чтобы на основании истинности или ложности простых высказываний определить истинность или ложность сложных высказываний.
Среди сложных высказываний можно выделить:
соединительные,
разделительные,
условные,
эквивалентные,
высказывания с внешним отрицанием.

Для булевых переменных определены следующие логические операции:
Инверсия (логическое отрицание)
 , , not, не, (неверно, что…)
2) Конъюнкция (логическое умножение)
, , &, and, и
3) Дизъюнкция (логическое сложение)
+, V, or, или
4) Импликация (следование) , если…, то…
5) Двойная импликация или эквиваленция
(равносильность) , =

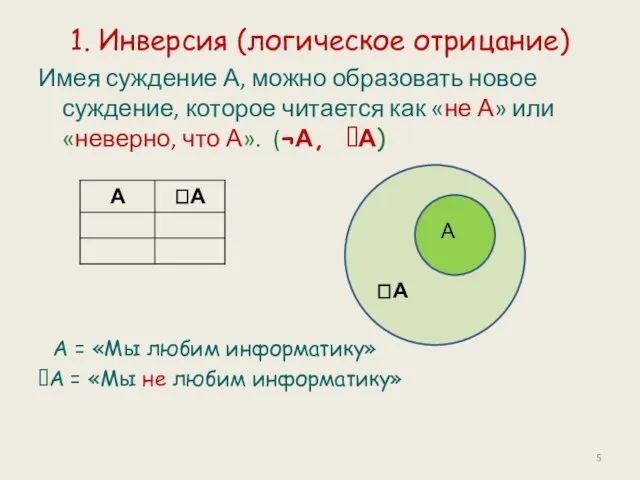
1. Инверсия (логическое отрицание)
Имея суждение А, можно образовать новое суждение, которое читается как «не А» или «неверно, что А». (А, А)
А = «Мы любим информатику»
А = «Мы не любим информатику»
А
А

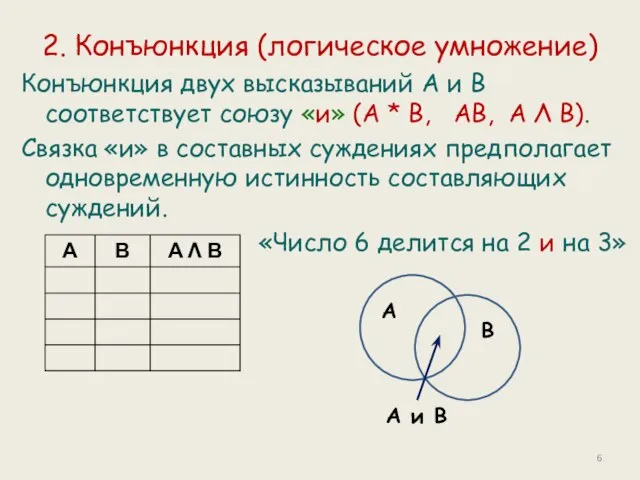
2. Конъюнкция (логическое умножение)
Конъюнкция двух высказываний А и В соответствует союзу «и» (А * В, АВ, А  В).
Связка «и» в составных суждениях предполагает одновременную истинность составляющих суждений.
«Число 6 делится на 2 и на 3»
А
В
А и В

3. Дизъюнкция (логическое сложение)
Дизъюнкция двух суждений соответствует союзу «или» (А + В, А V В).
Составное суждение со связкой «или» считается истинным, если истинно хотя бы одно из составных суждений, и считается ложным, если ложны все его составляющие.
Объединяющее «или»
«Петров является программистом или Петров является студентом»
А
В
А или В

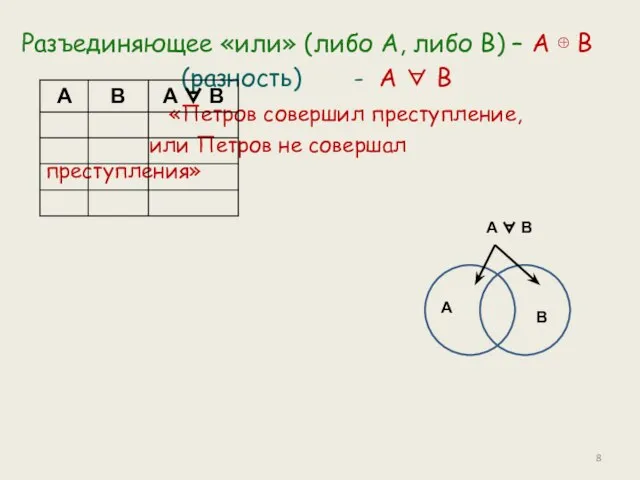
Разъединяющее «или» (либо А, либо В) – А  В
(разность) - А  В
«Петров совершил преступление,
или Петров не совершал преступления»
А
В
А  В

4. Импликация (следование)
А  В ( Если А, то В. Из А следует В)
Импликация ложна только в одном случае:
«из истины не может следовать ложь,
из лжи – все, что угодно».
«Если 2  2 = 5, то 2 + 2 = 5»
«Если 2  2 = 5, то 2 + 2 = 4»

Эквиваленция (равносильность, двойная импликация)
Суждения А и В называются равносильными или эквивалентными, если они одновременно истинны или одновременно ложны.
А = В ; А  В ; А  В ; А  В
А = «Этот треугольник равносторонний»
В = «Этот треугольник равноугольный»

Приоритетность логических операций
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция