Содержание
- 2. О практиках Работа в группах из 3-х человек. Постарайтесь сформировать группы, в которых будет хотя бы
- 3. Практика №1 «Программирование рекурсивных процедур и функций»
- 4. Основная задача Понять и реализовать 3 различных алгоритма нахождения чисел Фибоначчи. Подсказка: один алгоритм рекурсивный, два
- 5. Задача повышенной сложности Рекурсивно вычислить определитель матрицы разложением по строке/столбцу. Возможно ли вычислить итерационно? 19.09.2022 НИУ
- 6. Практика №2 «Продолжение работы с рекурсивными и итерационными алгоритмами»
- 7. Задача с прошлого занятия Рекурсивно вычислить определитель матрицы разложением по строке/столбцу. Возможно ли вычислить итерационно? 19.09.2022
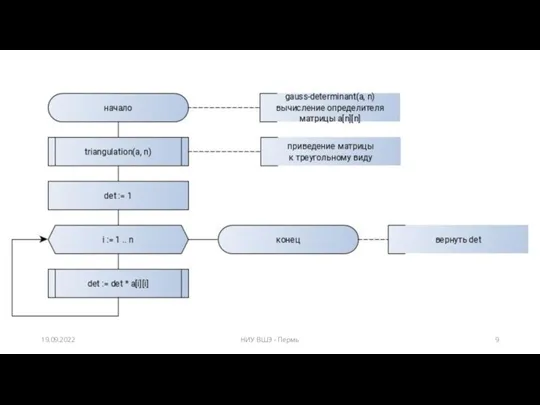
- 8. Задача на определитель матрицы Вычислить рекурсивно определитель матрицы с помощью метода Гаусса. Какой метод более точный
- 9. 19.09.2022 НИУ ВШЭ - Пермь
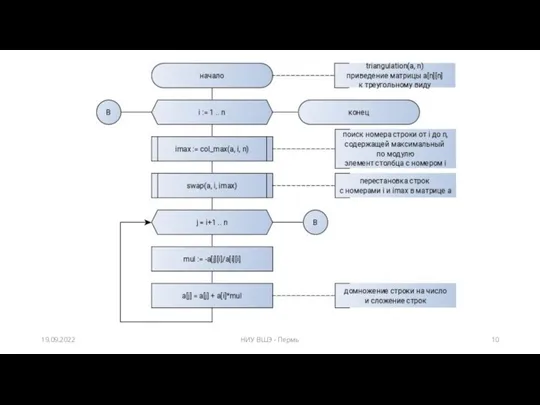
- 10. 19.09.2022 НИУ ВШЭ - Пермь
- 11. Практика №3 «Рекуррентные соотношения и итерационный алгоритм»
- 12. Задача по генерации перестановок Рекурсивная генерация всех n-факториал перестановок. Параметр n задаётся от 0 до 9.
- 13. Задача по генерации перестановок Например, найти все возможные перестановки для последовательности чисел 1, 2, 3. Существуют
- 14. Задача по генерации перестановок Дополнительно дублирую слайды с лекции: 19.09.2022 НИУ ВШЭ - Пермь
- 15. 19.09.2022 НИУ ВШЭ - Пермь
- 16. 19.09.2022 НИУ ВШЭ - Пермь
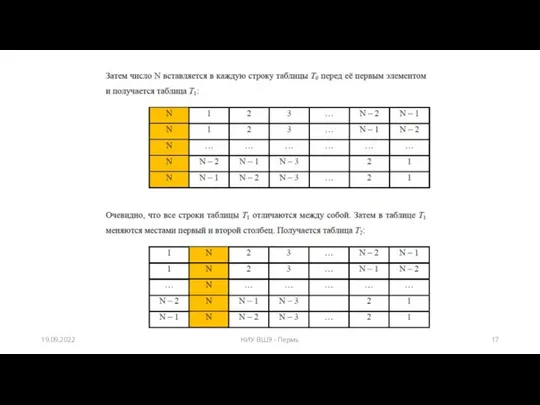
- 17. 19.09.2022 НИУ ВШЭ - Пермь
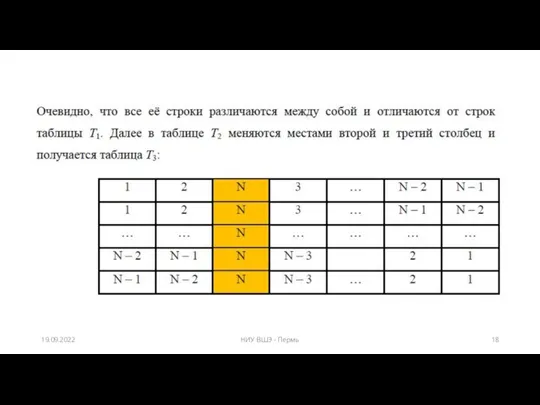
- 18. 19.09.2022 НИУ ВШЭ - Пермь
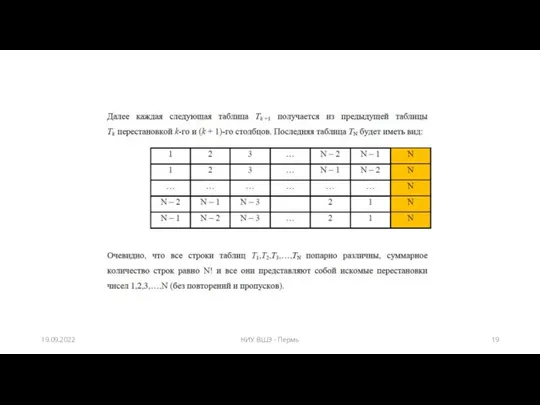
- 19. 19.09.2022 НИУ ВШЭ - Пермь
- 20. Задача по вычислению ленточного определителя Вычисление ленточного определителя (из презентации с лекции): итерационный способ; на основе
- 21. 19.09.2022 НИУ ВШЭ - Пермь
- 22. 19.09.2022 НИУ ВШЭ - Пермь
- 23. 19.09.2022 НИУ ВШЭ - Пермь
- 24. 19.09.2022 НИУ ВШЭ - Пермь
- 26. Скачать презентацию


















 Развитие и современное состояние МОУ «Подойниковская сош имени Героя Советского Союза М.И. Рогачёва»
Развитие и современное состояние МОУ «Подойниковская сош имени Героя Советского Союза М.И. Рогачёва» Коммуникационная политика в международном маркетинге
Коммуникационная политика в международном маркетинге История первой газеты и журнала
История первой газеты и журнала СРЕДСТВА ОБУЧЕНИЯ РУССКОМУ ЯЗЫКУ. ПРОБЛЕМА СОВРЕМЕННОГО УЧЕБНИКА
СРЕДСТВА ОБУЧЕНИЯ РУССКОМУ ЯЗЫКУ. ПРОБЛЕМА СОВРЕМЕННОГО УЧЕБНИКА Грибы в живописи
Грибы в живописи Профессиональные международные организации: новые возможности развития работ в области бетона и железобетона
Профессиональные международные организации: новые возможности развития работ в области бетона и железобетона Презентация на тему 8 Марта
Презентация на тему 8 Марта  Жлоб - грубый, тупой, малограмотный, некультурный, невоспитанный, наглый человек грубый, тупой, малограмотный, некультурный, невосп
Жлоб - грубый, тупой, малограмотный, некультурный, невоспитанный, наглый человек грубый, тупой, малограмотный, некультурный, невосп Аукцион объектов недвижимости
Аукцион объектов недвижимости Светотень в графике
Светотень в графике ОАО «Русские Навигационные Технологии» Лидер российского рынка мониторинга транспорта
ОАО «Русские Навигационные Технологии» Лидер российского рынка мониторинга транспорта Киево-Печерская Лавра-центр русского православия
Киево-Печерская Лавра-центр русского православия ЕГЭ по английскому языку
ЕГЭ по английскому языку СОВЕТСКАЯ МУЗЫКА
СОВЕТСКАЯ МУЗЫКА Презентация на тему Пресмыкающиеся
Презентация на тему Пресмыкающиеся  Макроэволюция
Макроэволюция Рамы металлические
Рамы металлические Владимирский верхошов
Владимирский верхошов Видеокарты
Видеокарты Буллинг в школе
Буллинг в школе Антиржавейная присадка
Антиржавейная присадка Зачем учить китайский
Зачем учить китайский Диверсифицированое ценообразование предприятия
Диверсифицированое ценообразование предприятия Презентация на тему Психология сновидений
Презентация на тему Психология сновидений  Виды глаголов
Виды глаголов Влияние солнечного излучения на показания комплекса АСДК-Б
Влияние солнечного излучения на показания комплекса АСДК-Б Влияние шума на здоровье человека
Влияние шума на здоровье человека Презентация на тему Влияние магнитных полей на живые организмы
Презентация на тему Влияние магнитных полей на живые организмы