А.М.Ковалев e-mail: [e-mail] , тел. [phone]

ПРОБЛЕМА
Изображение окружающей среды, получаемое от камеры с оптическим объективом (техническое зрение), не соответствует зрительному восприятию той же среды человеком (когнитивное зрение).
Искажения размеров, интерпозиции и глубины предметов могут превышать 100%.
Почему?

Ренессансная перспектива
Джотто (1266-1337) Альберти (1404-1472)
Брунеллески (1377-1446) Леонардо да Винчи (1452-1519)
Гиберти (1378-1455) Альбрехт Дюрер (1471-1528)
До сих пор является основным методом изображения трёхмерного (3М) пространства предметов

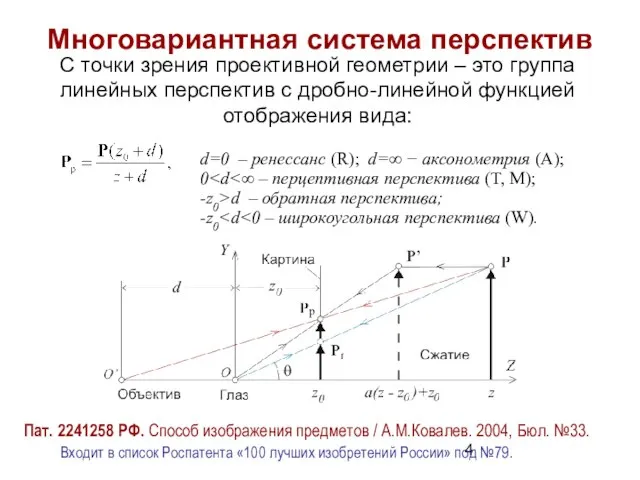
Многовариантная система перспектив
С точки зрения проективной геометрии – это группа линейных перспектив с дробно-линейной функцией отображения вида:
d=0 – ренессанс (R); d=∞ − аксонометрия (A);
0
-z0>d – обратная перспектива;
-z0
Пат. 2241258 РФ. Способ изображения предметов / А.М.Ковалев. 2004, Бюл. №33.
Входит в список Роспатента «100 лучших изобретений России» под №79.

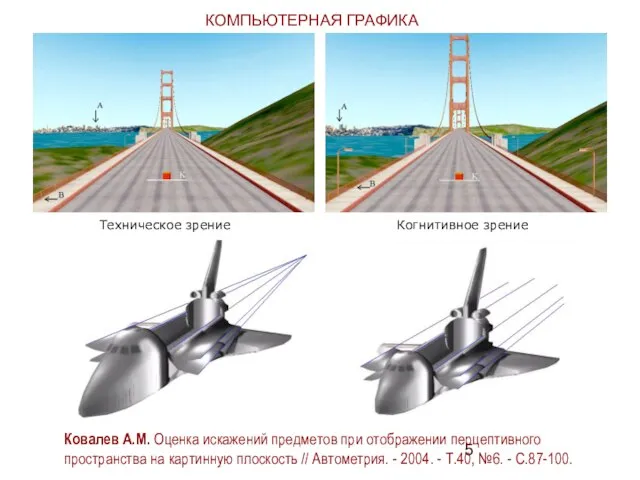
Техническое зрение
Когнитивное зрение
Ковалев А.М. Оценка искажений предметов при отображении перцептивного пространства на картинную плоскость // Автометрия. - 2004. - Т.40, №6. - С.87-100.
КОМПЬЮТЕРНАЯ ГРАФИКА

Недоступна фотографии
Линейная перспектива (М)
В такой манере рисовал
Поль Сезанн
Квазилинейная перспектива
Использует разные параметры dx,dy для разных координат картины.

Выводы
Многовариантная система перспектив даёт
возможность выбора оптимального варианта
для решения конкретной задачи.
Существование единой и непротиворечивой системы перспективы, в которой при изображении произвольной точки пространства все три её координаты определяются в полном соответствии с естественным зрительным восприятием,
на плоскости невозможно*.
*Ковалев А.М. О визуально воспринимаемом пространстве предметов
// Автометрия. - 2003. - Т.39, №6. - С.3-12.

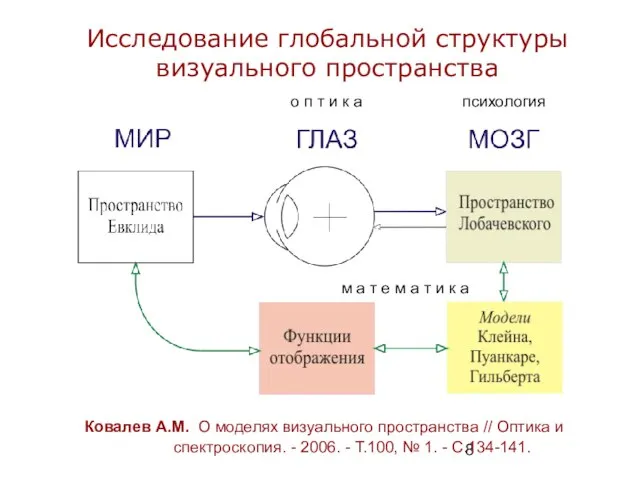
Исследование глобальной структуры
визуального пространства
Ковалев А.М. О моделях визуального пространства // Оптика и спектроскопия. - 2006. - Т.100, № 1. - С.134-141.
о п т и к а
психология
м а т е м а т и к а

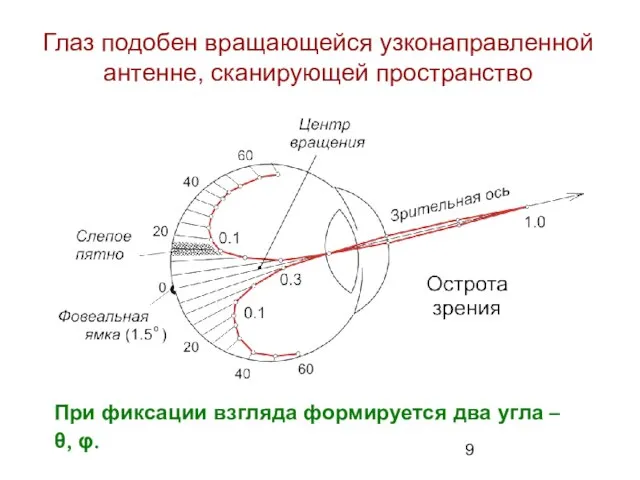
Глаз подобен вращающейся узконаправленной антенне, сканирующей пространство
При фиксации взгляда формируется два угла – θ, φ.

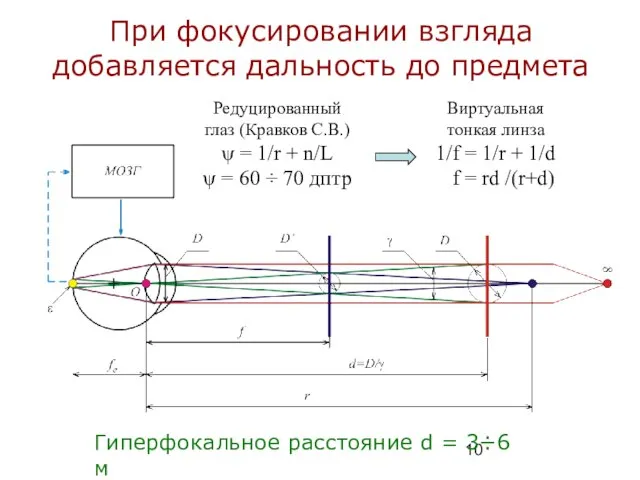
При фокусировании взгляда добавляется дальность до предмета
Гиперфокальное расстояние d = 3÷6 м
Редуцированный
глаз (Кравков С.В.)
ψ = 1/r + n/L
ψ = 60 ÷ 70 дптр
Виртуальная
тонкая линза
1/f = 1/r + 1/d
f = rd /(r+d)

Функции преобразования
МИР − геометрия Евклида r,θ,φ
Сенсорная модель* (Ф. Клейн) q=fm= ,θ,φ
p= ,θ,φ
Визуальное пространство* − геометрия Лобачевского
,θ,φ
(А. Пуанкаре)
Конформная модель*
*Ковалев А.М. Описание визуального пространства в моделях Клейна и Пуанкаре
// Автометрия. - 2006. - Т.42, № 4. - С.57-66.
Закон Вебера – Фехнера

Модель Клейна и визуальное пространство
Геометрия Лобачевского на плоскости
тождественна c геометрией на евклидовой
сфере с мнимым радиусом ic:
После подстановки z=iz получим
действительный гиперболоид
с асимптотическим конусом
Пересечение конуса и касательной
плоскости E (z=c) дает круг
Проекция всех точек гиперболоида на круг
и есть модель мнимой сферы Клейна.
Модель изотропного пространства – шар с радиусом с.

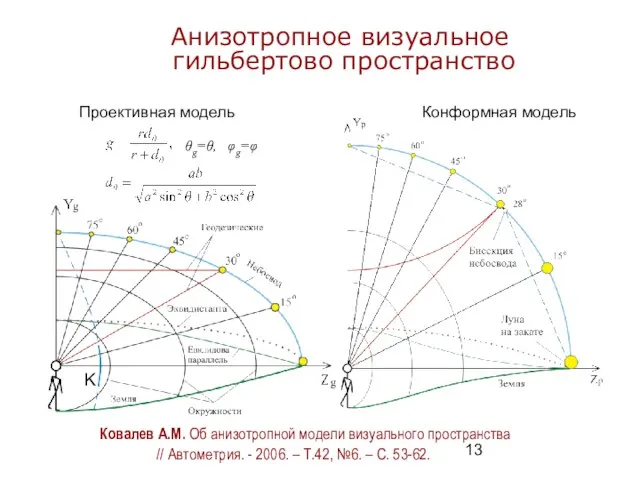
Анизотропное визуальное
гильбертово пространство
Проективная модель
Конформная модель
θg=θ, φg=φ
K
Ковалев А.М. Об анизотропной модели визуального пространства
// Автометрия. - 2006. – Т.42, №6. – С. 53-62.

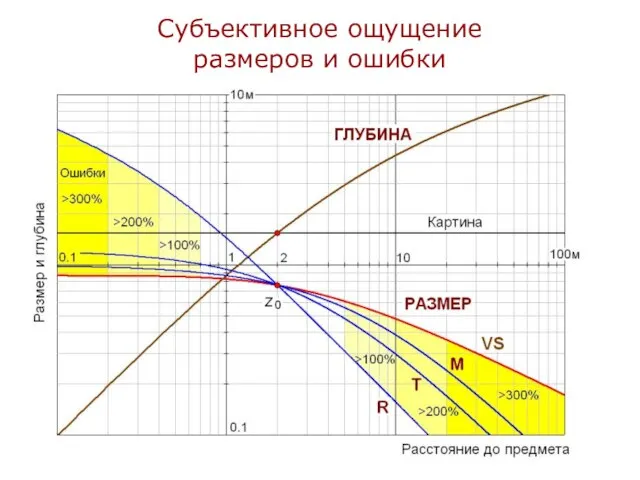
Субъективное ощущение
размеров и ошибки

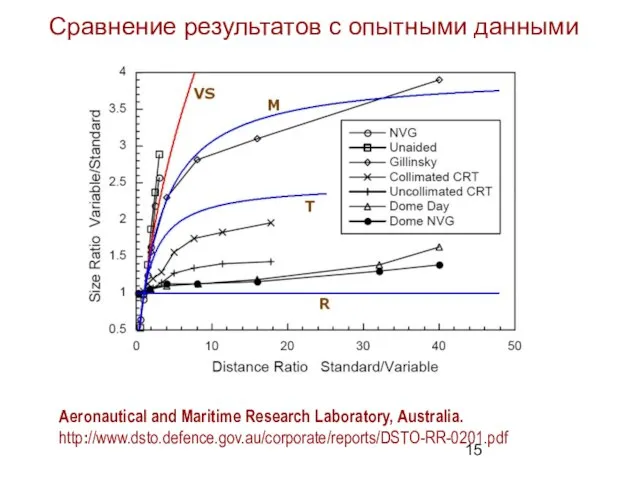
Aeronautical and Maritime Research Laboratory, Australia. http://www.dsto.defence.gov.au/corporate/reports/DSTO-RR-0201.pdf
Сравнение результатов с опытными данными

Заключение
Непротиворечивая система перспективы в полном соответствии с естественным зрительным восприятием существует в ограниченном объёме трехмерного пространства. Это − шар Клейна или эллипсоид Гильберта.
При конструировании «картинного» пространства (3М дисплеев) необходимо учитывать прямые признаки глубины, стимулирующие аккомодацию и конвергенцию глаз, а также все косвенные признаки, инициирующие когнитивный процесс сотворения визуального пространства.