Анализ информации в изображении

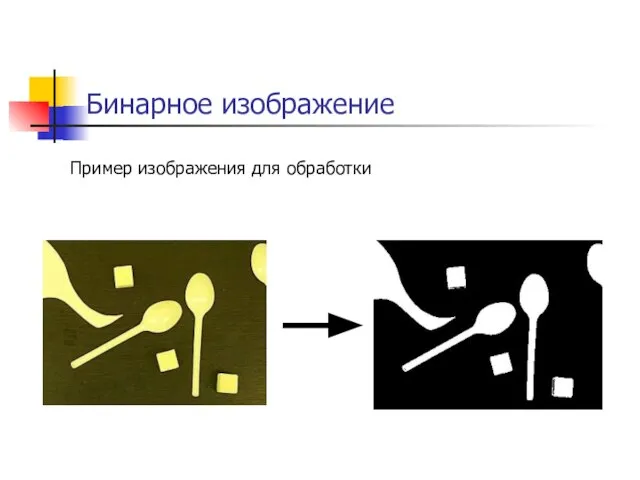
Бинарное изображение
Пример изображения для обработки

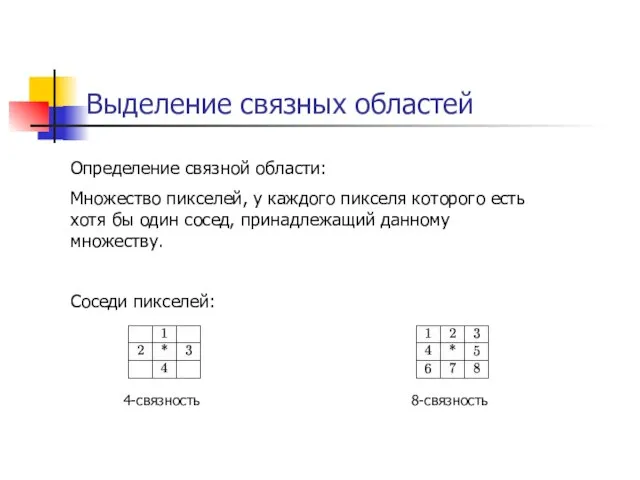
Выделение связных областей
Определение связной области:
Множество пикселей, у каждого пикселя которого есть хотя бы один сосед, принадлежащий данному множеству.
Соседи пикселей:
4-связность
8-связность

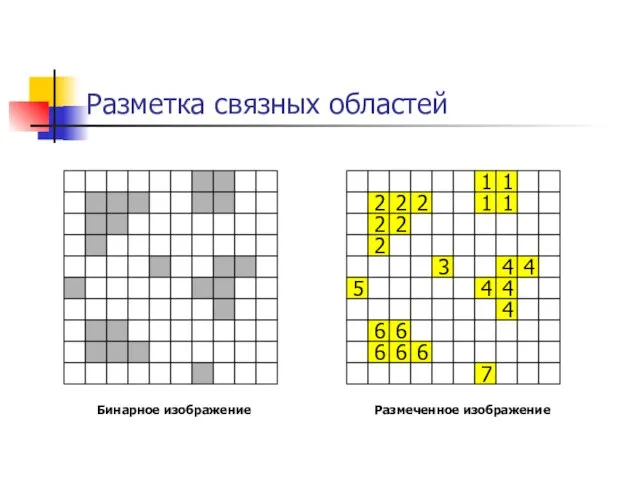
Разметка связных областей
1
1
2
2
2
1
1
2
2
2
3
4
4
5
4
4
4
6
6
6
6
6
7
Бинарное изображение
Размеченное изображение

Рекурсивная разметка связных областей 1
void Labeling(BIT* img[], int* labels[])
{
// labels должна быть обнулена
L = 1;
for(y = 0; y < H; y++)
for(x = 0; x < W; x++)
{
Fill(img, labels, x, y, L++);
}
}

Рекурсивная разметка связных областей 2
void Fill(BIT* img[], int* labels[], int x, int y, int L)
{
if( (labels[x][y] = = 0) && (img[x][y] = = 1) )
{
labels[x][y] = L;
if( x > 0 )
Fill(img, labels, x – 1, y, L);
if( x < W - 1 )
Fill(img, labels, x + 1, y, L);
if( y > 0 )
Fill(img, labels, x, y - 1, L);
if( y < H - 1 )
Fill(img, labels, x, y + 1, L);
}
}

Разметка связных областей путем последовательного сканирования
Последовательно, сканируем бинарное изображение сверху вниз,
слева направо:
if A = O
do nothing
else if (not B labeled) and (not C labeled)
increment label numbering and label A
else if B xor C labeled
copy label to A
else if B and C labeled
if B label = C label
copy label to A
else
copy either B label or C label to A
record equivalence of labels
Постобработка - переразметка с учетом эквивалентностей областей

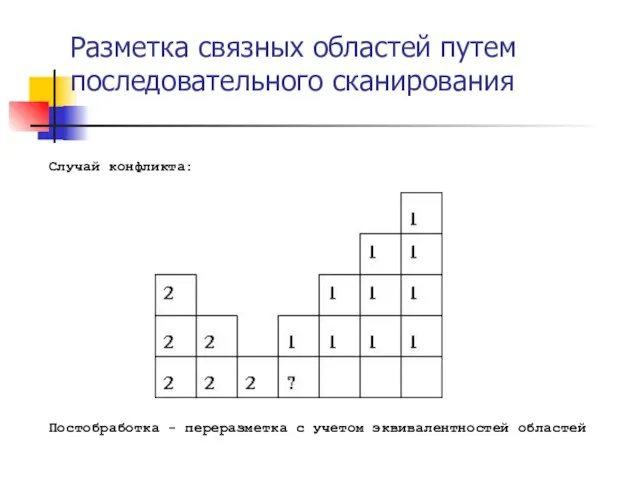
Разметка связных областей путем последовательного сканирования
Случай конфликта:
Постобработка - переразметка с учетом эквивалентностей областей

Анализ формы связных областей
Для каждой области можно подсчитать некий набор
простейших числовых характеристик:
Площадь
Периметр
Компактность
Ориентацию главной оси инерции
Удлиненность (эксцентриситет)
На основе этих характеристик можно классифицировать
получаемые области.

Анализ формы связных областей
Площадь – количество пикселей в области;
Периметр – количество пикселей принадлежащих
границе области;
Компактность – отношение квадрата периметра к площади;
Наиболее компактная фигура – круг,
.

Подсчет периметра области
Пиксель лежит на границе области, если он сам принадлежит
области и хотя бы один из его соседей области не принадлежит.
(внутренняя граница)
Пиксель лежит на границе области, если он сам не принадлежит
области и хотя бы один из его соседей области принадлежит.
(внешняя граница)
Периметр зависит также от того 4-х или 8-ми связность используется
для определения соседей.

Пример периметров области
Область
Внутренняя граница
Внешняя граница

Статистические моменты области
Дискретный центральный момент mij области определяется следующим образом:
n – общее количество пикселей в области

Инвариантные характеристики области
Для распознавания нас интересуют характеристики инвариантные по отношению к масштабированию, переносу, повороту:
Удлиненность, нецентрированность (эксцентриситет)
Компактность

Ориентация главной оси инерции
Не является инвариантной к повороту, но в ряде случаев предоставляет полезную информацию об ориентации объекта:

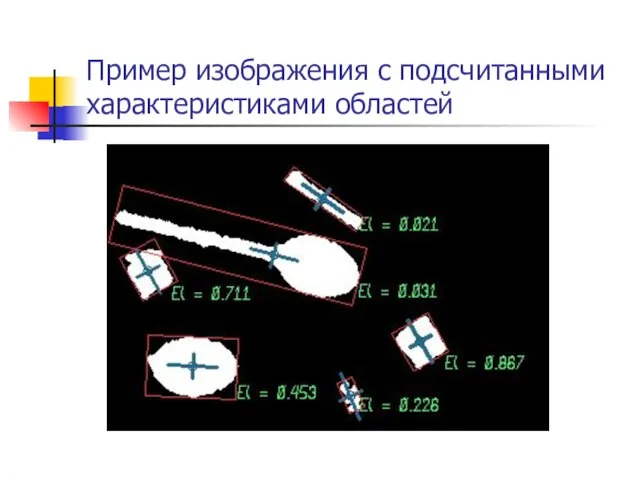
Пример изображения с подсчитанными характеристиками областей

Другие инвариантные характеристики области

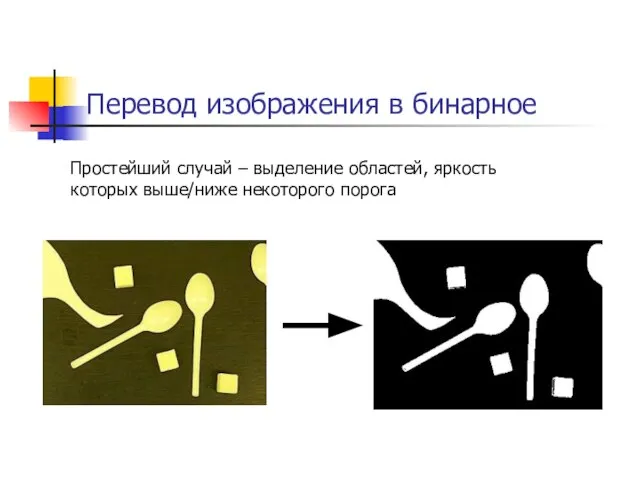
Перевод изображения в бинарное
Простейший случай – выделение областей, яркость которых выше/ниже некоторого порога

Как автоматически вычислить порог?
Сегментация изображения на области однородной яркости методом k-средних.
Метод k-средних – метод кластеризации данных, строящий кластеры настолько различные, насколько это возможно.
Целью задачи кластеризации является разбиение множества объектов на классы (кластеры) на основе некоторой меры сходства объектов (в нашем случае мера сходства это близость яркостей пикселей).

Алгоритм k-средних
Дано:
Набор векторов xi i=1,…,p;
k – число кластеров, на которые нужно разбить набор xi;
Найти:
k средних векторов mj j=1,…,k (центров кластеров);
отнести каждый из векторов xi к одному из k кластеров;

Алгоритм k-средних
Случайным образом выбрать k средних mj j=1,…,k;
Для каждого xi i=1,…,p подсчитать расстояние до каждого из mj j=1,…,k,
Отнести (приписать) xi к кластеру j’, расстояние до центра которого mj’ минимально;
Пересчитать средние mj j=1,…,k по всем кластерам;
Повторять шаги 2, 3 пока кластеры не перестанут изменяться;

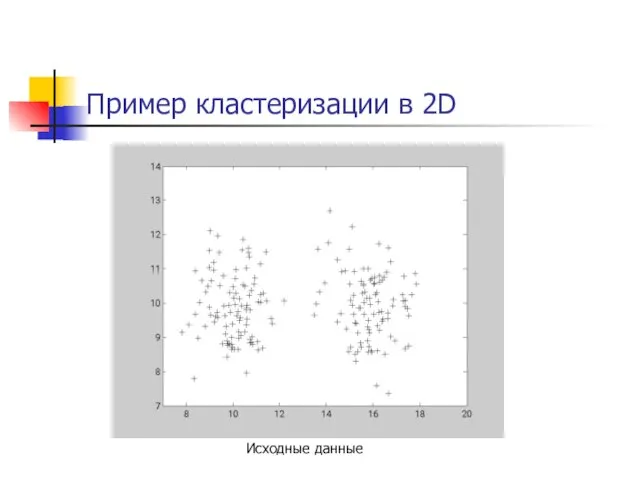
Пример кластеризации в 2D
Исходные данные

Пример кластеризации в 2D
Случайная инициализация центров кластеров (шаг 1)

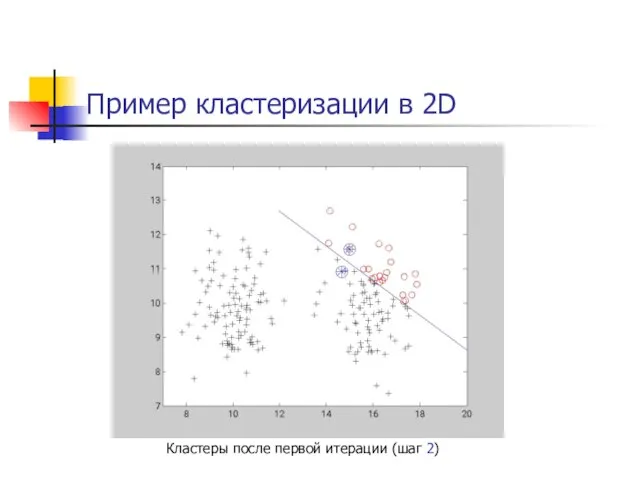
Пример кластеризации в 2D
Кластеры после первой итерации (шаг 2)

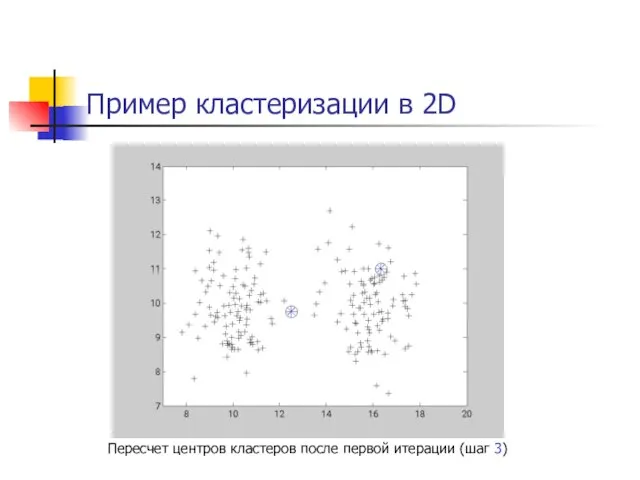
Пример кластеризации в 2D
Пересчет центров кластеров после первой итерации (шаг 3)

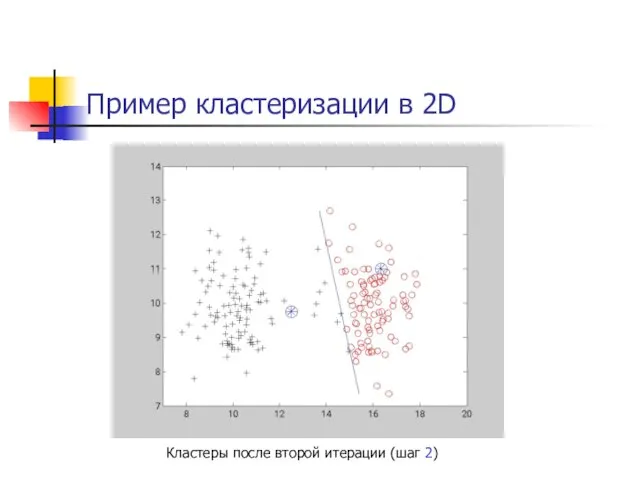
Пример кластеризации в 2D
Кластеры после второй итерации (шаг 2)

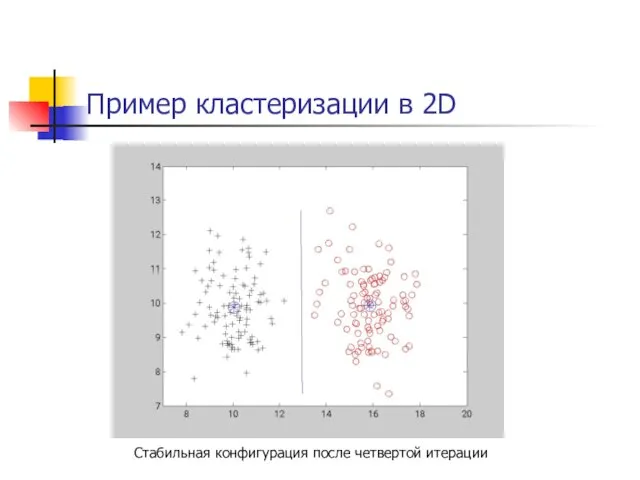
Пример кластеризации в 2D
Стабильная конфигурация после четвертой итерации

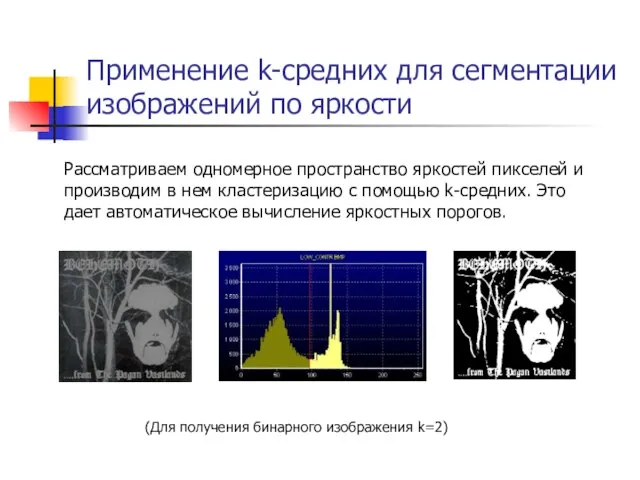
Применение k-средних для сегментации изображений по яркости
Рассматриваем одномерное пространство яркостей пикселей и производим в нем кластеризацию с помощью k-средних. Это дает автоматическое вычисление яркостных порогов.
(Для получения бинарного изображения k=2)

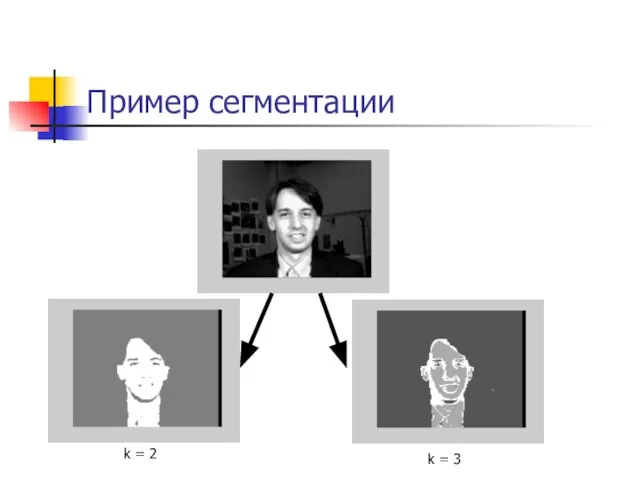
Пример сегментации
k = 2
k = 3

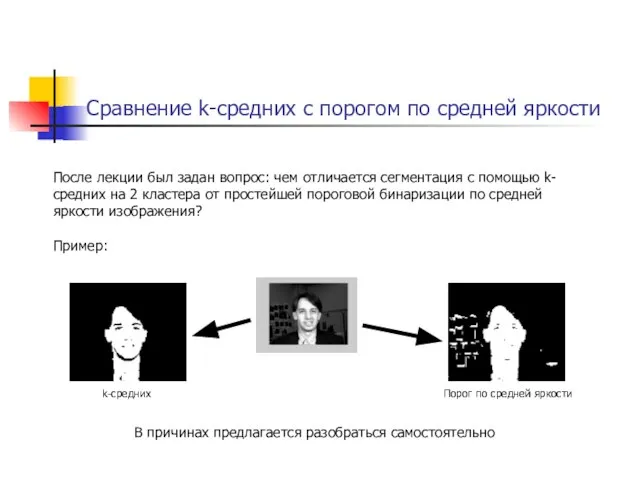
Сравнение k-средних с порогом по средней яркости
После лекции был задан вопрос: чем отличается сегментация с помощью k-средних на 2 кластера от простейшей пороговой бинаризации по средней яркости изображения?
Пример:
k-средних
Порог по средней яркости
В причинах предлагается разобраться самостоятельно

Преобразование Хафа (Hough)
Преобразование Хафа позволяет находить на бинарном изображении плоские кривые, заданные параметрически, например: прямые, окружности, эллипсы, и т.д.
Бинарное изображение – изображение, пиксели которого принимают всего два значения (0 и 1). Считаем 0 – точками фона, 1 – «точками интереса».
Задача преобразования Хафа состоит в выделении кривых, образованных точками интереса.

Основная идея метода
Рассмотрим семейство кривых на плоскости, заданное параметрическим уравнением:
F(a1, a2, …, an, x, y) = 0;
где F - некоторая функция, a1, a2, ..., an - параметры семейства кривых, x, y - координаты на плоскости. Параметры семейства кривых образуют фазовое пространство, каждая точка которого (конкретные значения параметров a1, a2, ..., an) соответствует некоторой кривой.
Идея преобразования Хафа состоит в поиске кривых (точек фазового пространства), которые проходят через достаточное количество точек интереса.

Машинное представление
Ввиду дискретности машинного представления и входных данных (изображения), требуется перевести непрерывное фазовое пространство в дискретное.
Вводим сетку на фазовом пространстве
Каждой ячейке сетки ставим в соответствие счетчик
Значение счетчика каждой ячейки устанавливаем равным количеству точек интереса, через которые проходит хотя бы одна кривая, параметры которой принадлежат данной ячейке.
Анализ счетчиков ячеек позволяет найти на изображении кривые, на которых лежит наибольшее количество точек интереса.

Выделение прямых на изображении
Прямую на плоскости можно задать следующим образом:
x cosθ + y sinθ = R,
R - длина перпендикуляра опущенного на прямую из начала координат,
θ - угол между перпендикуляром к прямой и осью OX,
θ изменяется в пределах от 0 до 2π , R ограничено размерами входного изображения.

Выделение прямых на изображении
Таким образом функция, задающая семейство прямых,
имеет вид:
F (R, θ, x, y) = x cosθ + y sinθ - R.
Через каждую точку (x, y) изображения можно провести несколько прямых с разными R и θ, то есть каждой точке (x, y) изображения соответствует набор точек в фазовом пространстве (R, θ). В свою очередь каждой точке пространства (R, θ) соответствует набор точек (x, y) на изображении, образующий прямую.

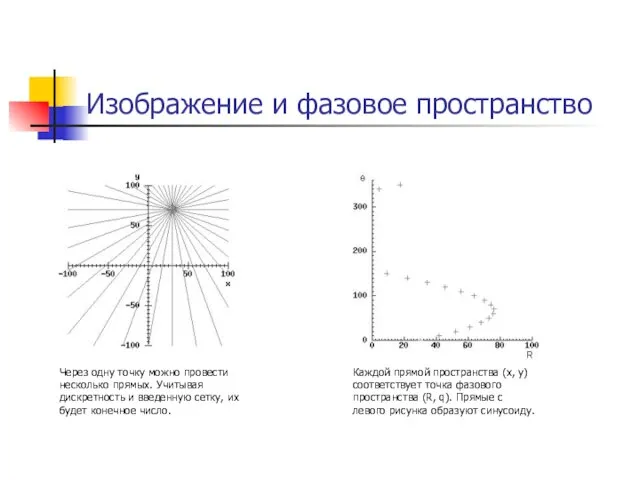
Изображение и фазовое пространство
Через одну точку можно провести несколько прямых. Учитывая дискретность и введенную сетку, их будет конечное число.
Каждой прямой пространства (x, y) соответствует точка фазового пространства (R, q). Прямые с левого рисунка образуют синусоиду.

Изображение и фазовое пространство
Изображение с пятью точками интереса.
Кривые в фазовом пространстве, соответствующие множеству прямых проходящих через каждую из точек.
Точки пересечения кривых в фазовом пространстве соответствуют параметрам прямых, проходящих более чем через одну точку интереса.

Дискретизация фазового пространства
Переводим непрерывное фазовое пространство в дискретное. Введем сетку на пространстве (R, θ), одной ячейке которой соответствует набор прямых с близкими значениями R и θ.
Счетчик ставится в соответствие каждой ячейке сетки
[Ri, Ri+1]x[θi,θi+1], равный числу точек интереса на изображении, удовлетворяющих уравнению:
x cosθ + y sinθ = R, где θi ≤ θ ≤ θi+1, Ri ≤ R ≤ Ri+1.

Алгоритм выделения прямых
обнулить счетчики всех ячеек;
для каждой точки интереса на изображении:
для каждой прямой, проходящей через данную точку увеличить соответствующий счетчик;
выбрать ячейки со значением счетчика, превышающим заданный порог;
В общем случае алгоритм поиска прямой на изображении при помощи преобразования Хафа выглядит так:

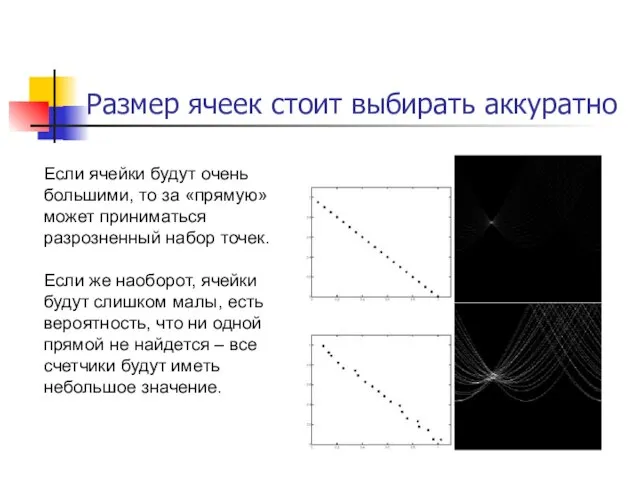
Размер ячеек стоит выбирать аккуратно
Если ячейки будут очень большими, то за «прямую» может приниматься разрозненный набор точек.
Если же наоборот, ячейки будут слишком малы, есть вероятность, что ни одной прямой не найдется – все счетчики будут иметь небольшое значение.

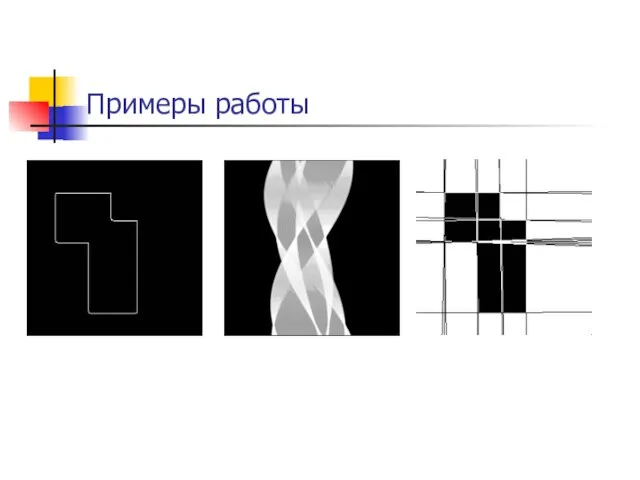
Примеры работы

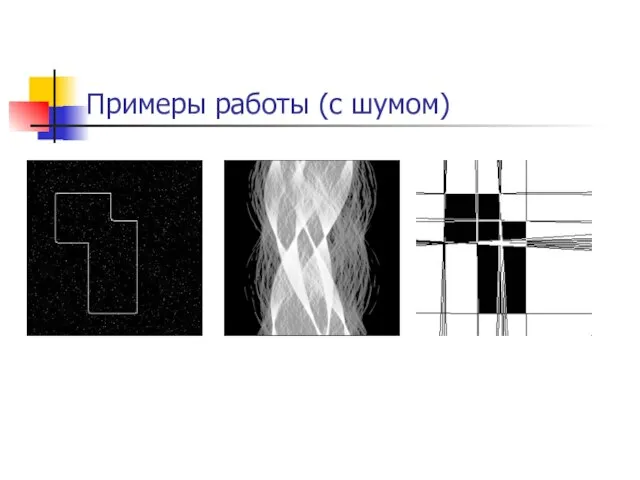
Примеры работы (с шумом)