Аннуитетные платежи

Задача № 1.
31.01.2016г Пётр взял в банке некоторую сумму в кредит под 12% годовых.
Схема выплаты кредита следующая:
31.01. каждого следующего года банк начисляет проценты на оставшуюся часть долга (т.е. долг возрастает на 12%), затем Пётр переводит в банк 3512320 рублей. Какую сумму взял Пётр в банке, если он выплатил долг тремя равными платежами?

Задача № 2.

Задача № 3.
2017 год

Задача № 4.

Задача № 5.

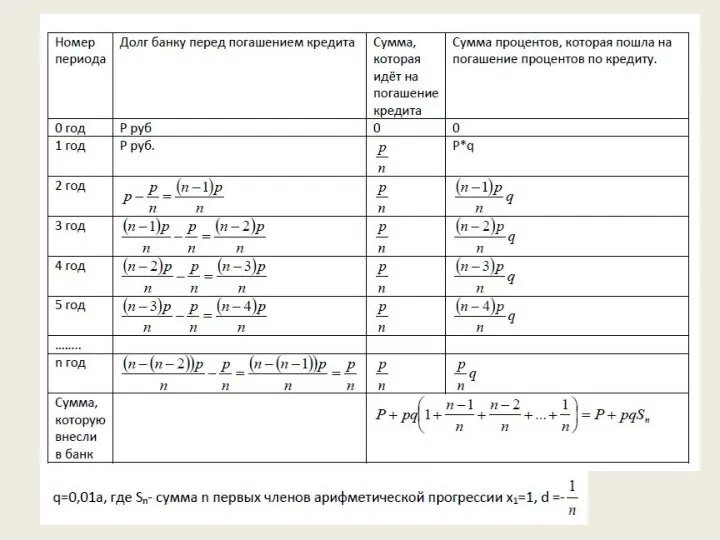
Суммы, выплачиваемые в конец каждого …(временного периода), подбираются так, чтобы сумма долга каждый месяц уменьшалась равномерно,т.е. на одну и ту же величину.
Дифференцированный платеж — это ежемесячный платеж по кредиту, уменьшающийся к концу срока кредитования и состоит из выплачиваемой постоянной доли основного долга и процентов на невыплаченный остаток кредита
ЗАДАЧА. Пусть взят кредит p рублей под а % годовых
с дифференцированным платежом на n лет (временных периодов).

Задача № 6.

Эльвира взяла кредит 1 млн. руб. на срок 36 мес. По договору она должна возвращать банку часть денег в конце каждого месяца.
Каждый месяц общая сумма долга возрастает на 10 %, а затем уменьшается на сумму, уплаченную Эльвирой банку в конце месяца. Суммы, выплаченные Эльвирой, подбираются так, чтобы сумма долга уменьшалась равномерно, т.е. на одну и ту же величину каждый месяц. На сколько тысяч рублей больше Эльвира выплатит банку в течение первого года кредитования, нежели в течение третьего года?
Задача № 7. Александр Ларин вар.141

Бизнесмен взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма долга увеличивается на 12 %, а затем уменьшается на сумму, уплаченную бизнесменом банку в конце месяца. Суммы, выплаченные бизнесменом, подбираются так, чтобы сумма долга уменьшалась равномерно, т.е. на одну и ту же величину каждый месяц. Сколько процентов от суммы кредита составила сумма, уплаченная банку сверх номы?
Задача № 8.

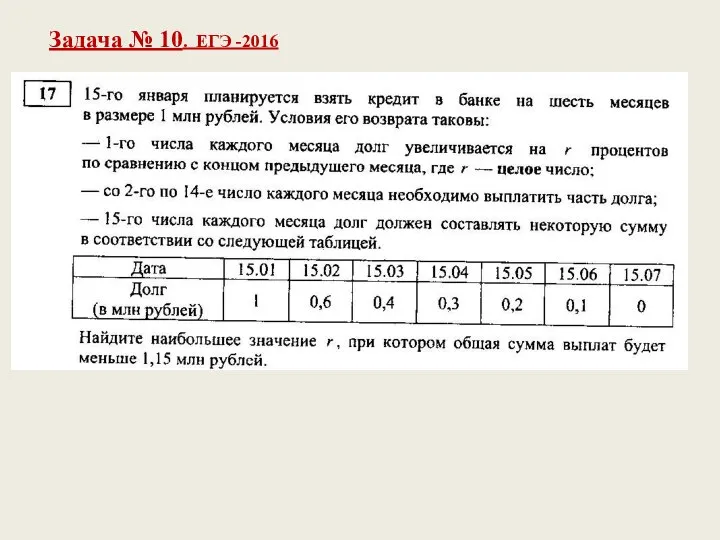
15 января планируется взять кредит в банке на 19 месяцев.
Условия возврата таковы: - 1-го числа каждого месяца долг возрастает на q% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 –е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 30 % больше суммы, взятой в кредит. Найдите q.
Задача № 9. ЕГЭ -2015

Задача № 10. ЕГЭ -2016

Задача № 11. ЕГЭ -2016

Тема 6. Анализ согласованности проверки заданий с развернутым ответом

Тема 6. Анализ согласованности проверки заданий с развернутым ответом
1 балл
Задание 7

Тема 6. Анализ согласованности проверки заданий с развернутым ответом
2 балла
Задание 8

Тема 6. Анализ согласованности проверки заданий с развернутым ответом
0 баллов
Задание 9

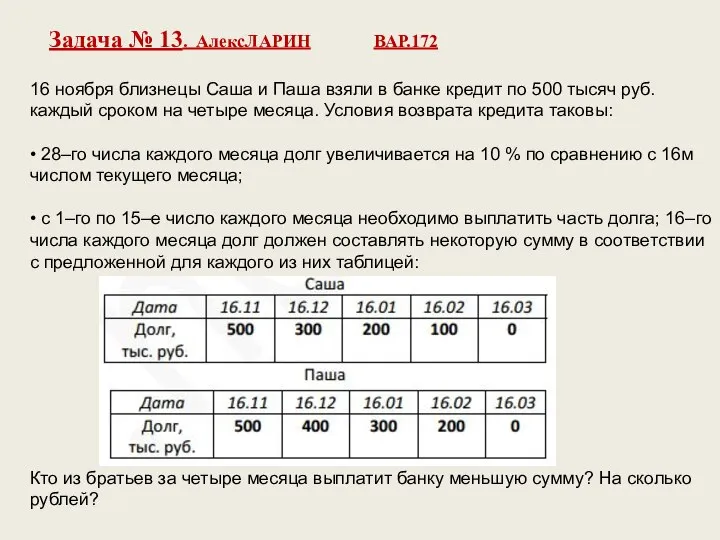
16 ноября близнецы Саша и Паша взяли в банке кредит по 500 тысяч руб. каждый сроком на четыре месяца. Условия возврата кредита таковы:
• 28–го числа каждого месяца долг увеличивается на 10 % по сравнению с 16м числом текущего месяца;
• с 1–го по 15–е число каждого месяца необходимо выплатить часть долга; 16–го числа каждого месяца долг должен составлять некоторую сумму в соответствии с предложенной для каждого из них таблицей:
Кто из братьев за четыре месяца выплатит банку меньшую сумму? На сколько рублей?
Задача № 13. АлексЛАРИН ВАР.172

Име­ет­ся три па­ке­та акций. Общее сум­мар­ное ко­ли­че­ство акций пер­вых двух па­ке­тов сов­па­да­ет с общим ко­ли­че­ством акций в тре­тьем па­ке­те. Пер­вый пакет в 4 раза де­шев­ле вто­ро­го, а сум­мар­ная сто­и­мость пер­во­го и вто­ро­го па­ке­тов сов­па­да­ет со сто­и­мо­стью тре­тье­го па­ке­та. Одна акция из вто­ро­го па­ке­та до­ро­же одной акции из пер­во­го па­ке­та на ве­ли­чи­ну, за­клю­чен­ную в пре­де­лах от 16 тыс. руб. до 20 тыс. руб., а цена акции из тре­тье­го па­ке­та не мень­ше 42 тыс. руб. и не боль­ше 60 тыс. руб. Опре­де­ли­те, какой наи­мень­ший и наи­боль­ший про­цент от об­ще­го ко­ли­че­ства акций может со­дер­жать­ся в пер­вом па­ке­те.
Задача № 14.

Задача № 15.

Задача № 16

Задача № 17

В рас­по­ря­же­нии на­чаль­ни­ка име­ет­ся бри­га­да ра­бо­чих в со­ста­ве 24 че­ло­век. Их нужно рас­пре­де­лить на день на два объ­ек­та. Если на пер­вом объ­ек­те ра­бо­та­ет t че­ло­век, то их су­точ­ная зар­пла­та со­став­ля­ет 4t2 у. е. Если на вто­ром объ­ек­те ра­бо­та­ет t че­ло­век, то их су­точ­ная зар­пла­та со­став­ля­ет t2 у. е. Как нужно рас­пре­де­лить на эти объ­ек­ты бри­га­ду ра­бо­чих, чтобы вы­пла­ты на их су­точ­ную зар­пла­ту ока­за­лись наи­мень­ши­ми? Сколь­ко у. е. в этом слу­чае при­дет­ся за­пла­тить ра­бо­чим?
Задача № 18 Ларин №123

Гри­го­рий яв­ля­ет­ся вла­дель­цем двух за­во­дов в раз­ных го­ро­дах. На за­во­дах про­из­во­дят­ся аб­со­лют­но оди­на­ко­вые то­ва­ры, но на за­во­де, рас­по­ло­жен­ном во вто­ром го­ро­де, ис­поль­зу­ет­ся более со­вер­шен­ное обо­ру­до­ва­ние. В ре­зуль­та­те, если ра­бо­чие на за­во­де, рас­по­ло­жен­ном в пер­вом го­ро­де, тру­дят­ся сум­мар­но t2 часов в не­де­лю, то за эту не­де­лю они про­из­во­дят 3t еди­ниц то­ва­ра; если ра­бо­чие на за­во­де, рас­по­ло­жен­ном во вто­ром го­ро­де, тру­дят­ся сум­мар­но t2 часов в не­де­лю, то за эту не­де­лю они про­из­во­дят 4t еди­ниц то­ва­ра.
За каж­дый час ра­бо­ты (на каж­дом из за­во­дов) Гри­го­рий пла­тит ра­бо­че­му 500 руб­лей.
Гри­го­рий готов вы­де­лять 5 000 000 руб­лей в не­де­лю на опла­ту труда ра­бо­чих. Какое наи­боль­шее ко­ли­че­ство еди­ниц то­ва­ра можно про­из­ве­сти за не­де­лю на этих двух за­во­дах?
Задача № 19.

В двух об­ла­стях есть по 20 ра­бо­чих, каж­дый из ко­то­рых готов тру­дить­ся
по 10 часов в сутки на до­бы­че алю­ми­ния или ни­ке­ля.
В пер­вой об­ла­сти один ра­бо­чий за час
до­бы­ва­ет 0,1 кг алю­ми­ния или 0,1 кг ни­ке­ля.
Во вто­рой об­ла­сти для до­бы­чи х кг алю­ми­ния в день тре­бу­ет­ся
че­ло­ве­ко-часов труда, а для до­бы­чи у кг ни­ке­ля в день
тре­бу­ет­ся че­ло­ве­ко-часов труда.
Обе об­ла­сти по­став­ля­ют до­бы­тый ме­талл на завод,
где для нужд про­мыш­лен­но­сти про­из­во­дит­ся сплав алю­ми­ния и ни­ке­ля,
в ко­то­ром на 3 кг алю­ми­ния при­хо­дит­ся 1 кг ни­ке­ля.
При этом об­ла­сти до­го­ва­ри­ва­ют­ся между собой вести
до­бы­чу ме­тал­лов так,
чтобы завод мог про­из­ве­сти наи­боль­шее ко­ли­че­ство спла­ва.
Сколь­ко ки­ло­грам­мов спла­ва при таких усло­ви­ях
еже­днев­но смо­жет про­из­ве­сти завод?
Задача № 20.

Задача № 21.

Задача № 22.

Стоимость разработки электронной версии учебника некоторого издания равна 800 тыс. рублей. Затраты на производство х тысяч таких электронных учебников
в этом издательстве равны (x2+6x+22100) тысяч рублей в год. Если учебники продавать по цене а руб. за единицу, то прибыль издательства за один год составит ax–(x2+6x+22100).
Издательство будет выпускать учебники в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении а разработка учебника окупится не более чем за 2 года?
Задача № 23.

Два ве­ло­си­пе­ди­ста рав­но­мер­но дви­жут­ся по вза­им­но пер­пен­ди­ку­ляр­ным до­ро­гам по на­прав­ле­нию к пе­ре­крест­ку этих дорог. Один из них дви­жет­ся со ско­ро­стью 40 км/ч и на­хо­дит­ся на рас­сто­я­нии 5 км от пе­ре­крест­ка, вто­рой дви­жет­ся со ско­ро­стью 30 км/ч и на­хо­дит­ся на рас­сто­я­нии 3 км от пе­ре­крест­ка. через сколь­ко минут рас­сто­я­ние между ве­ло­си­пе­ди­ста­ми ста­нет наи­мень­шим? Ка­ко­во будет это наи­мень­шее рас­сто­я­ние.

Алек­сей вышел из дома на про­гул­ку со ско­ро­стью v км/ч. После того, как он про­шел 6 км, из дома сле­дом за ним вы­бе­жа­ла со­ба­ка Жучка, ско­рость ко­то­рой была на 9 км/ч боль­ше ско­ро­сти Алек­сея. Когда Жучка до­гна­ла хо­зя­и­на, они по­вер­ну­ли назад и вме­сте воз­вра­ти­лись домой со ско­ро­стью 4 км/ч. Най­ди­те зна­че­ние v, при ко­то­ром время про­гул­ки Алек­сея ока­жет­ся наи­мень­шим. Сколь­ко при этом со­ста­вит время его про­гул­ки?