Слайд 23.2.1Точечный источник и контакт двух сред
Обозначим:
Будем искать решение
в виде:
Г.У.:
На границе:

Слайд 3Коэффициент отражения:
Решение:
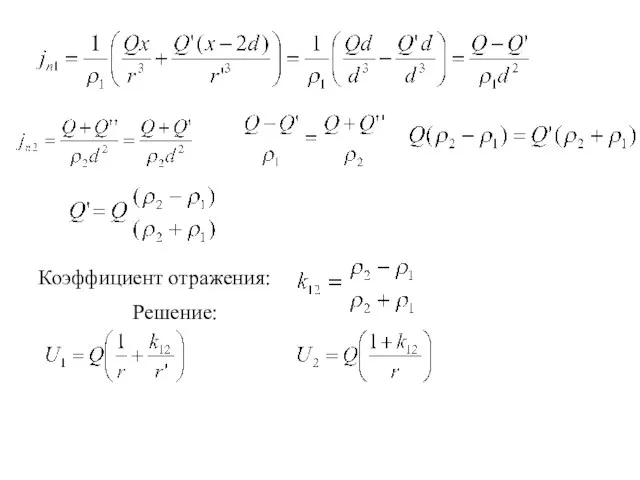
Слайд 4Дифференцирование по направлению х
дает поле, отвечающее идеальной градиент-установке
На поверхности земли:

Слайд 5Проведем преобразования применительно к случаю
профилирования:
A
ρ1
ρ2
d
Ο
x’
x
0
1.
x’
0
A
ρ1
ρ2
Ο
2.
A
ρ1
ρ2
d
Ο
x’
0
3.
1.
2.
3.

Слайд 6Формулы для кажущегося сопротивления идеальной градиент-установки
ΑΜΝ:
MNB:

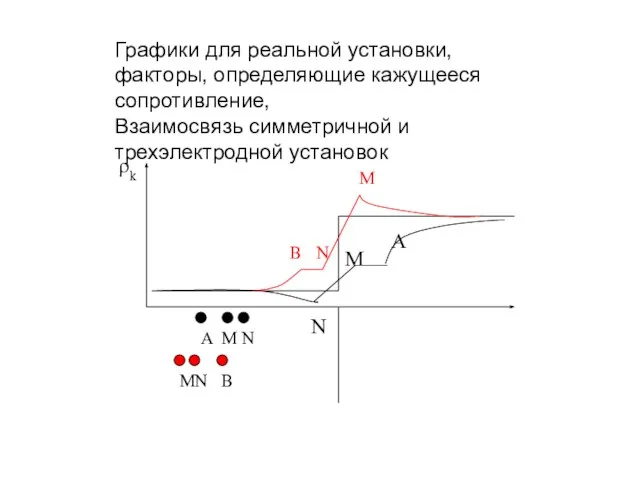
Слайд 7ρk
N
M
A
B
N
M
Графики для реальной установки, факторы, определяющие кажущееся сопротивление,
Взаимосвязь симметричной и трехэлектродной установок
Слайд 83.2.2. Сфера в электрическом поле
Постановка задачи:
Разрыв радиальной компоненты E
(при неразрывности тангенциальной)

Слайд 9Положим, что
*
**
Уравнение
Лежандра
Используем метод разделения переменных:

Слайд 10Уравнение Лежандра имеет нетривиальные решения при:
Решения уравнения – полиномы Лежандра, определяемые по

формуле Родрига:
-частные решения
Вернемся к уравнению **
Слайд 11Ему удовлетворяют решения:
Частное решение:
Объединяем решения:
Общее решение:

Слайд 12Для rДля r>d:
Для окрестностей шара: rПредварительно представим 1/R с помощью полиномов Лежандра

Слайд 133б)
Решение уравнений 3а и 3б:
- коэффициент отражения

Слайд 14Частный случай однородного поля:
R
M
r
d
a
ρ2
ρ1
d>>r r/d<<1
d>>a a/d<<1
R
A→

Слайд 15Ограничимся первым членом ряда, т.к. d – большая величина

Слайд 16r
x
Θ
Сопоставление с полем диполя:
1
Μ
− нормальное поле

Слайд 17Выводы:
Сферическое включение в однородном поле эквивалентно электрическому диполю, помещенному в центре сферы.

Физическими источниками аномального поля являются индуцированные источники, расположенные на поверхности включения.
Для шар-проводника внутреннее поле направлено как нормальное поле, для шара-изолятора – направлено противоположно нормальному полю.

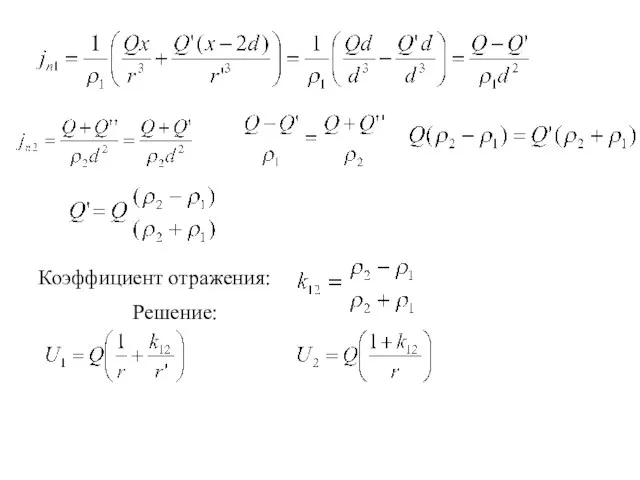














 Нелитературные формы языка
Нелитературные формы языка Панкреатит у собак. выполнила:Филимонова Д. научный руководитель:Паршин П.А.
Панкреатит у собак. выполнила:Филимонова Д. научный руководитель:Паршин П.А. Спортивно-оздоровительныйкомплекс БГУ «Бригантина» 15-17 февраля 2008 г.
Спортивно-оздоровительныйкомплекс БГУ «Бригантина» 15-17 февраля 2008 г. Процессуальное право
Процессуальное право Владимир Михайлович Ануфриев
Владимир Михайлович Ануфриев Презентация на тему Вероисповедание
Презентация на тему Вероисповедание  ЗЕМСНАРЯДЫ С ШНЕКОВЫМИ НАГНЕТАТЕЛЯМИ ДЛЯ ДОБЫЧИ САПРОПЕЛЯ ИЗ ОТКРЫТЫХ ВОДОЕМОВ
ЗЕМСНАРЯДЫ С ШНЕКОВЫМИ НАГНЕТАТЕЛЯМИ ДЛЯ ДОБЫЧИ САПРОПЕЛЯ ИЗ ОТКРЫТЫХ ВОДОЕМОВ 25% МИРОВОГО ПРОИЗВОДСТВА дымовых пожарных извещателей
25% МИРОВОГО ПРОИЗВОДСТВА дымовых пожарных извещателей Презентация на тему Тютчев Фёдор Иванович (1803 – 1873)
Презентация на тему Тютчев Фёдор Иванович (1803 – 1873)  Анализ конкурентов и принятие решения о модели монетизации программы “CoronaHunt”
Анализ конкурентов и принятие решения о модели монетизации программы “CoronaHunt” Альберт Эйнштейн
Альберт Эйнштейн Анализ возможных погрешностей при испытаниях конструкций. Виды ошибок измерений и способы их определения и устранения
Анализ возможных погрешностей при испытаниях конструкций. Виды ошибок измерений и способы их определения и устранения Выполнение положений Московского областного отраслевого соглашения по машиностроительному и горно-металлургическому комплекса
Выполнение положений Московского областного отраслевого соглашения по машиностроительному и горно-металлургическому комплекса Уроки про офис
Уроки про офис Глава 2Основы алгоритмизациии объектно-ориентированногопрограммирования
Глава 2Основы алгоритмизациии объектно-ориентированногопрограммирования ТРЦ Балашовский пассаж
ТРЦ Балашовский пассаж Совершенствование системы оказания медицинской помощи больным середечно-сосудистыми заболеваниями в Российской Федерации ЗАМ
Совершенствование системы оказания медицинской помощи больным середечно-сосудистыми заболеваниями в Российской Федерации ЗАМ Курьер доставляющего сервиса Чекбокс. Тренинг
Курьер доставляющего сервиса Чекбокс. Тренинг ОФБУ как форма управления активами
ОФБУ как форма управления активами Курица с морковкой и луком
Курица с морковкой и луком москалев долг
москалев долг “Внутренний контроль качества образования. Поиск оптимальной модели. Опыт работы по организации внутришкольного контроля ”
“Внутренний контроль качества образования. Поиск оптимальной модели. Опыт работы по организации внутришкольного контроля ”  Презентация на тему А.С. Пушкин "Медный Всадник"
Презентация на тему А.С. Пушкин "Медный Всадник" Публичная власть на региональном уровне и правовые основы государственной власти в субъектах Российской Федерации
Публичная власть на региональном уровне и правовые основы государственной власти в субъектах Российской Федерации Проект: Признание недействительным решения налогового органа
Проект: Признание недействительным решения налогового органа Historical Foundations of Modern English Spelling
Historical Foundations of Modern English Spelling ЭТО
ЭТО Реклама на сайте Dirty.ru для украинских рекламодателей
Реклама на сайте Dirty.ru для украинских рекламодателей