Содержание
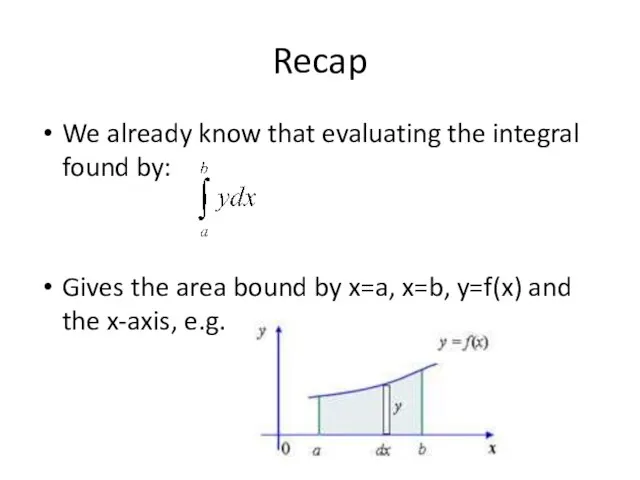
- 2. Recap We already know that evaluating the integral found by: Gives the area bound by x=a,
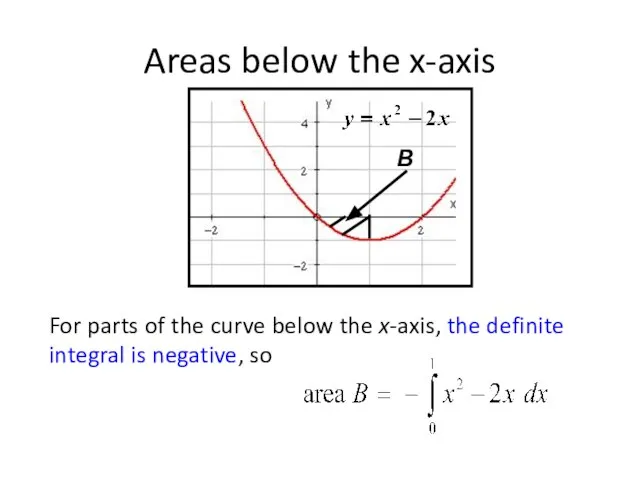
- 3. Areas below the x-axis
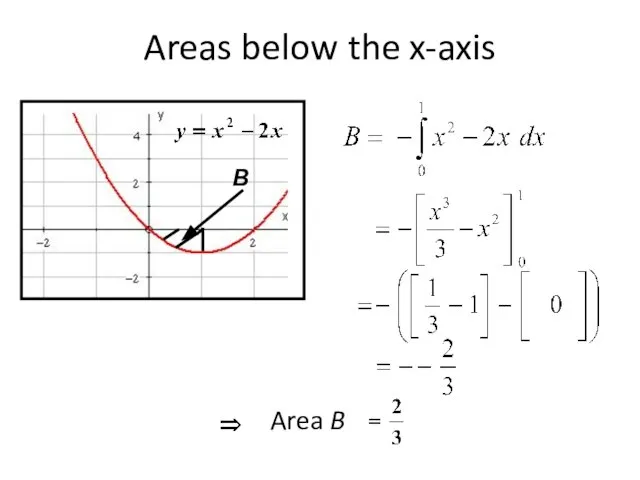
- 4. Areas below the x-axis
- 5. An area is always positive. The definite integral is positive for areas above the x-axis but
- 6. Example Evaluate: We can see that the function has 3 roots at: x = -1, x
- 7. Example Our knowledge of a positive cubic function tells us that the section between the limits
- 8. Example So the total area is given by:
- 9. Areas bound with the y-axis We can also evaluate areas bound by y=a, y=b, x=f(y) and
- 10. Example Find this area bound by y=1, y=3, y=√(x-2) and the y-axis. Firstly we need to
- 12. Скачать презентацию






 Рекомендации по работе с детьми алаликами
Рекомендации по работе с детьми алаликами ГОУ «Школа – интернат №15 циркового профиля для детей – сирот и детей, оставшихся без попечения родителей, имени Ю.В.Никулина»
ГОУ «Школа – интернат №15 циркового профиля для детей – сирот и детей, оставшихся без попечения родителей, имени Ю.В.Никулина» Что изучает физика
Что изучает физика Без географии Вы нигде!!!
Без географии Вы нигде!!! Три основные задачи на проценты
Три основные задачи на проценты Открытый урок: учить и учиться
Открытый урок: учить и учиться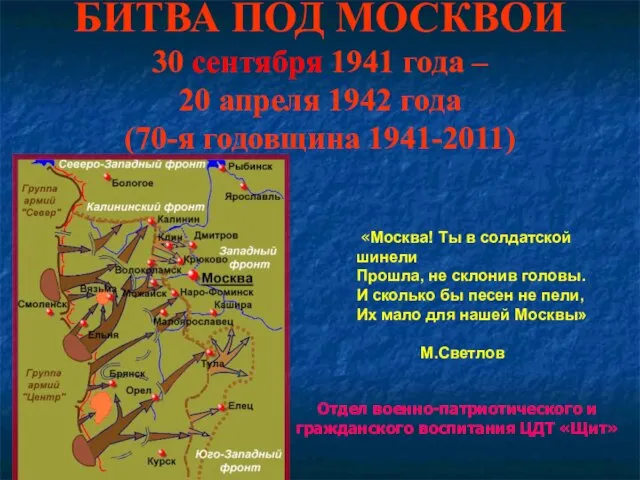 БИТВА ПОД МОСКВОЙ30 сентября 1941 года – 20 апреля 1942 года(70-я годовщина 1941-2011)
БИТВА ПОД МОСКВОЙ30 сентября 1941 года – 20 апреля 1942 года(70-я годовщина 1941-2011) Круговая тренировка на уроках физической культуры
Круговая тренировка на уроках физической культуры Презентация на тему виды изобразительного искусства
Презентация на тему виды изобразительного искусства  ПРОВЕДЕНИЕ ГОСУДАРСТВЕННОЙ (ИТОГОВОЙ) АТТЕСТАЦИИ ВЫПУСКНИКОВ IX КЛАССОВ В НОВОЙ ФОРМЕ В 2012 ГОДУ
ПРОВЕДЕНИЕ ГОСУДАРСТВЕННОЙ (ИТОГОВОЙ) АТТЕСТАЦИИ ВЫПУСКНИКОВ IX КЛАССОВ В НОВОЙ ФОРМЕ В 2012 ГОДУ  РА Fabrika - Презентация
РА Fabrika - Презентация 오늘 저는 선미하고 극장에 가서 영화를 보았습니다
오늘 저는 선미하고 극장에 가서 영화를 보았습니다 Презентация на тему Подготовка к сочинению. Описание местности
Презентация на тему Подготовка к сочинению. Описание местности Уникальное шоу Мыльная кухня
Уникальное шоу Мыльная кухня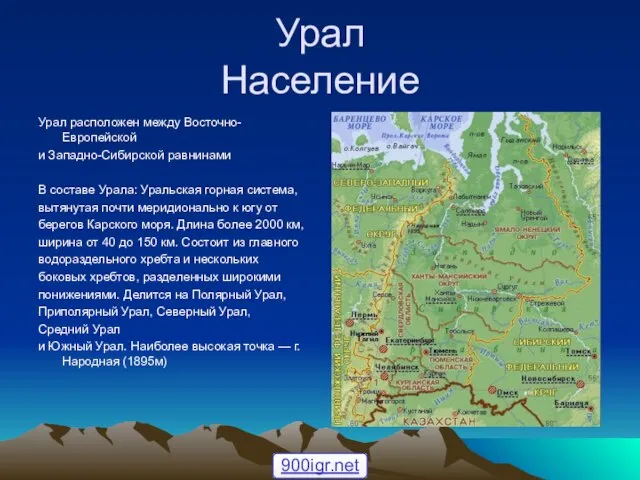 Население Урала
Население Урала Приготовление изделий из слоёного теста. 7 класс
Приготовление изделий из слоёного теста. 7 класс Механизмы финансирования деятельности по адаптации к последствиям изменений климата и снижению выбросов парниковых газов
Механизмы финансирования деятельности по адаптации к последствиям изменений климата и снижению выбросов парниковых газов Клинический случай. Операция
Клинический случай. Операция Инженер-строитель
Инженер-строитель Фёдор Михайлович Достоевский 1821 - 1881
Фёдор Михайлович Достоевский 1821 - 1881 Разновидности компьютерных сетей
Разновидности компьютерных сетей Тема проекта: Русская народная игрушка
Тема проекта: Русская народная игрушка ЗДОРОВЬЕСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ
ЗДОРОВЬЕСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ Полезащитное лесоразведение
Полезащитное лесоразведение Электронное взаимодействие между организациями ислужбой занятости населения
Электронное взаимодействие между организациями ислужбой занятости населения Преимущества и выгоды внедрения отраслевых систем бизнес-анализа на платформе Microsoft
Преимущества и выгоды внедрения отраслевых систем бизнес-анализа на платформе Microsoft Проблемы воспитания
Проблемы воспитания Сода
Сода