Содержание
- 2. Георг Кантор (3 марта 1845г. – 6 января 1918г.) Георг Фердинанд Людвиг Филипп Кантор родился 3
- 3. Два года спустя он занял должность приват-доцента в Университете в Галле . Один из его коллег
- 4. Шарль Мерэ (1835г – 1811г.) В 1869 году Мерэ опубликовал статью, в которой было впервые дано
- 5. Чтобы определить иррациональное число как предел последовательности рациональных чисел, нужно показать, что такая последовательность сходится. Для
- 6. Теория действительного числа В своем построении Кантор исходит из наличия рациональных чисел. Затем он вводит фундаментальные
- 7. Далее, формальные пределы равны друг другу, если они имеют две такие фундаментальные последовательности, которые эквивалентны друг
- 8. Отношение порядка определяется следующим образом. Если и то Если то Отношение порядка
- 9. Таким образом, классы эквивалентности описывают некоторые вещественные числа. Назовем их вещественными числами первого порядка. Если мы
- 11. Скачать презентацию








 Морской флот. Морской транспорт и его деятельность
Морской флот. Морской транспорт и его деятельность Ресторан и мини-гольф клуб Мелисса Флеминг
Ресторан и мини-гольф клуб Мелисса Флеминг Электронагревательные приборы. 8 класс
Электронагревательные приборы. 8 класс Не поддаваться панике
Не поддаваться панике Бозгурд. Терроризм
Бозгурд. Терроризм Презентация на тему Развитие сюжетной игры детей дошкольного возраста
Презентация на тему Развитие сюжетной игры детей дошкольного возраста Инновационные подходы к социально-воспитательной работе с детьми с ограниченными возможностями здоровья
Инновационные подходы к социально-воспитательной работе с детьми с ограниченными возможностями здоровья Продукция
Продукция Пути развития современной архитектуры. Основные стили архитектуры ХХ-ХXI века. 7 класс
Пути развития современной архитектуры. Основные стили архитектуры ХХ-ХXI века. 7 класс Страны Южной Америки
Страны Южной Америки МОУ "Берёзовская средняя общеобразовательная школа №2"
МОУ "Берёзовская средняя общеобразовательная школа №2" Презентация на тему Симметрия в архитектуре
Презентация на тему Симметрия в архитектуре  Protected Area Governance
Protected Area Governance  Что такое фольклор?
Что такое фольклор? Культурные практики ребенка
Культурные практики ребенка Основы трудового права
Основы трудового права  Инновационная экосистема
Инновационная экосистема Реконкиста и образование централизованных государств на Пиренейском полуострове
Реконкиста и образование централизованных государств на Пиренейском полуострове Птицы
Птицы Особенности органищации БУ в группах
Особенности органищации БУ в группах Архитектура Акрополя
Архитектура Акрополя Правописание безударных личных окончаний глаголов I и I I спряжения
Правописание безударных личных окончаний глаголов I и I I спряжения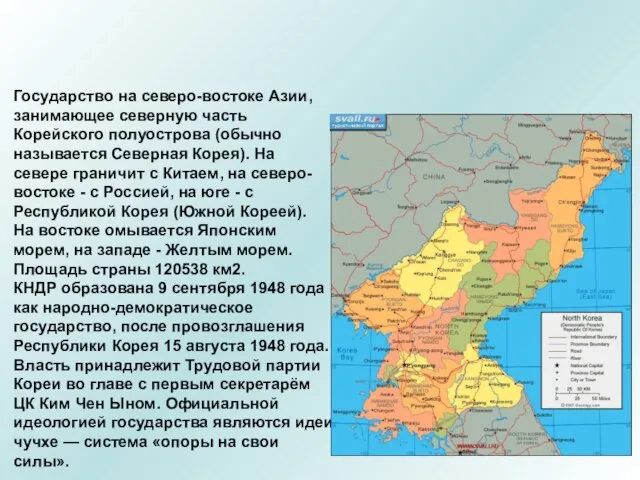 Презентация на тему СЕВЕРНАЯ КОРЕЯ (КОРЕЙСКАЯ НАРОДНО-ДЕМОКРАТИЧЕСКАЯ РЕСПУБЛИКА)
Презентация на тему СЕВЕРНАЯ КОРЕЯ (КОРЕЙСКАЯ НАРОДНО-ДЕМОКРАТИЧЕСКАЯ РЕСПУБЛИКА)  Нормативно-правовое обеспечение организации производственного контроля на молокоперерабатывающих предприятиях
Нормативно-правовое обеспечение организации производственного контроля на молокоперерабатывающих предприятиях Типы смесителей. Лекция №10
Типы смесителей. Лекция №10 Безопасный вебсерфинг
Безопасный вебсерфинг Курообразные
Курообразные Группа «Дюймовочка»
Группа «Дюймовочка»