Статистическая гипотеза

Нулевой (основной) гипотезой - H0 называют какое-либо конкретное предположение о теоретической функции распределения или предположение, влекущее за собой важные практические последствия
Альтернативная гипотеза H1 - любая гипотеза, исключающая нулевую

Задача проверки статистической гипотезы состоит в том, чтобы, используя статистические данные (выборку)
X1, X2, …, Xn,
принять или отклонить нулевую гипотезу

Нулевые и альтернативные гипотезы формулируются как утверждение о принадлежности функций распределения некоторой случайной величины определенному классу распределений

Гипотеза называется простой, если соответствующий класс распределений содержит лишь одно распределение, в противном случае гипотеза будет сложной.
Гипотезы о параметрах распределений называются
параметрическими

значение которой для заданной
выборки служит основанием принятия или отклонения основной гипотезы
Статистикой критерия
называется функция от выборки

Статистический критерий - правило, позволяющее только по результатам наблюдений
X1, X2, …, Xn
принять или отклонить нулевую гипотезу H0

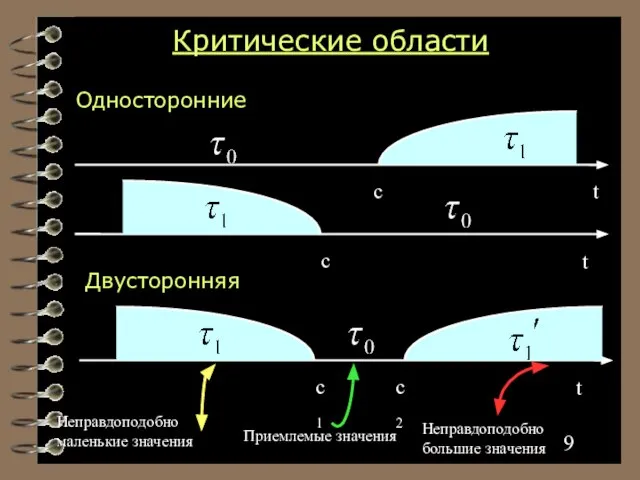
Каждому критерию отвечает разбиение области значений статистики критерия на две непересекающихся части: критическую область τ1
область принятия гипотезы τ0

Критические области
Двусторонняя
Неправдоподобно маленькие значения
Неправдоподобно большие значения
Приемлемые значения

Если значение статистики критерия попадает в область принятия гипотезы τ0 , то принимается нулевая гипотеза, в противном случае она отвергается (принимается альтернативная гипотеза)

Задать статистический критерий значит:
задать статистику критерия
задать критическую область

В ходе проверки гипотезы H0 можно прийти к правильному выводу, либо совершить два рода ошибок:
ошибку первого рода -- отклонить H0, когда она верна
ошибку второго рода -- принять H0, когда она не верна.

Так как статистика критерия
есть случайная величина со своим законом распределения, то
попадание её в ту или иную область характеризуется соответствующими вероятностями:
вероятностью ошибки первого рода α
вероятностью ошибки второго рода β

Ошибку первого рода α ещё называют уровнем значимости критерия.
Часто пользуются понятием мощности критерия W -- вероятности попадания в критическую область при условии справедливости альтернативной гипотезы

В общем случае вводят функцию мощности

При разработке статистического критерия невозможно одновременно минимизировать обе ошибки. Поэтому поступают следующим образом: при заданном числе испытаний n устанавливается верхняя граница для ошибки первого рода α.
Выбирается тот критерий, у которого наименьшая ошибка второго рода.

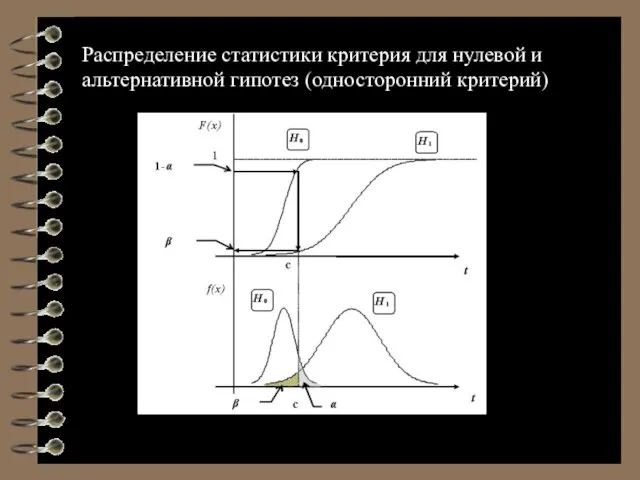
Распределение статистики критерия для нулевой и альтернативной гипотез (односторонний критерий)

Уровень значимости α устанавливается из значений следующего ряда:
0.05, 0.01, 0.005, …
события с такими вероятностями считаются практически невозможными.
Допустимая величина уровня значимости определяется теми последствиями, которые наступают после совершения ошибки.

Примеры формулировок статистических гипотез
Гипотеза о виде распределения:
произведено n независимых измерений случайной величины с неизвестной функцией распределения F(x). Следует проверить гипотезу:

Гипотеза однородности
Произведено k серий независимых испытаний
Можно ли с достаточной надежностью считать, что закон распределения наблюдений от серии к серии не менялся? Если это так, то статистические данные однородны.
Проверяется гипотеза однородности:

Гипотеза независимости
Наблюдается двухмерная случайная величина ξ = (ξ1, ξ2) с неизвестной функцией распределения Fξ (x, y) и есть основания полагать, что компоненты
ξ1, ξ2 -- независимы.
В этом случае проверяется гипотеза независимости:

1 шаг – выдвигается основная гипотеза H0
2 шаг – задается уровень значимости α
3 шаг – задается статистика критерия T(X) с известным законом распределения
Пять шагов проверки гипотезы

4 шаг – из таблиц распределения статистики критерия находятся квантили, соответствующие границам критической области
5 шаг – для данной выборки рассчитывается значение статистики критерия

Если значение статистики критерия попадает в область принятия гипотезы, то нулевая гипотеза принимается на уровне значимости α.
В противном случае принимается альтернативная гипотеза (отвергается нулевая гипотеза)

Среди критериев выделяются такие, которые улавливают любые отклонения от нулевой гипотезы.
Они называются
« критерии согласия »

Критерий согласия Колмогорова
Применяется для проверки гипотезы о виде распределения
При условии, что теоретическая функция распределения непрерывная и полностью определена

Критерий согласия Колмогорова
За меру близости распределений принимается максимальное отклонение эмпирической функции распределения Fn(x) от теоретической F(x).

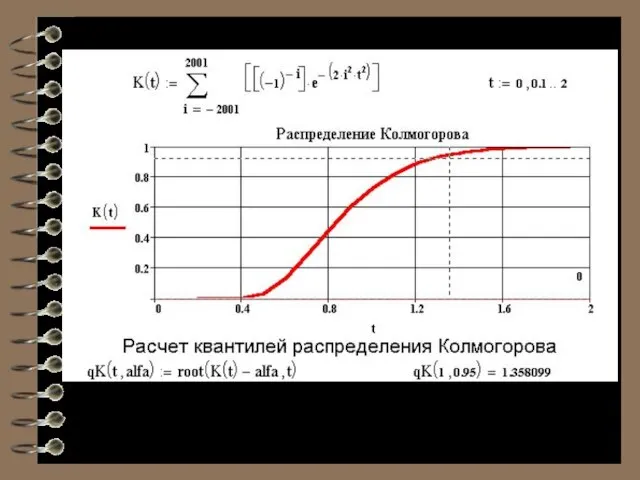
Распределение статистики Колмогорова не зависит от F (x).
При больших n оно стремится к распределению Колмогорова.
Статистика критерия

Критерий согласия χ2 Пирсона
(хи-квадрат)
Первоначально разработан для дискретных распределений