Арксинус. Решение уравнения sin t = a (10 класс)

Цели
Изучить определение арксинуса числа.
Изучить формулы решения простейшего тригонометрического уравнения sin t = a.

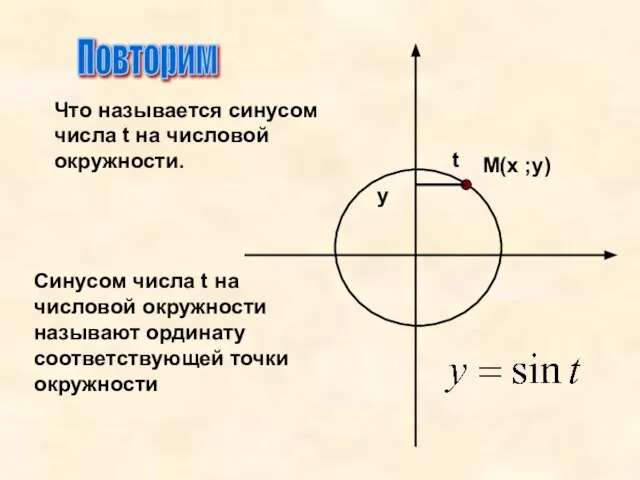
Повторим
Что называется синусом числа t на числовой окружности.
Синусом числа t на числовой окружности называют ординату соответствующей точки окружности
М(х ;у)
у
t

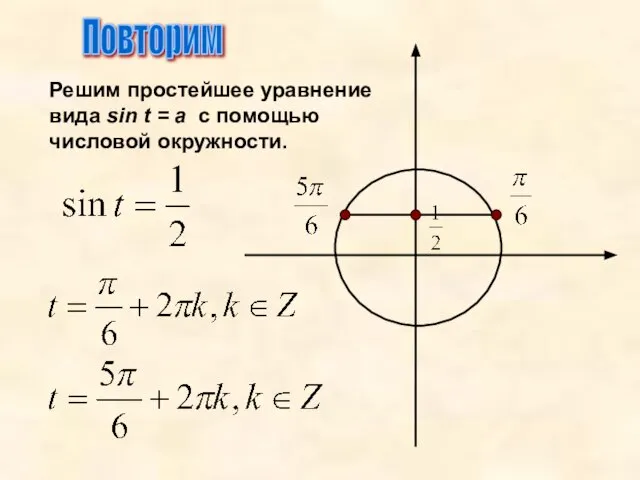
Повторим
Решим простейшее уравнение вида sin t = a с помощью числовой окружности.

Решим уравнение
С помощью числовой окружности получим решение.

?
Решим уравнение
Что это за число t1?
В рассмотрение введён новый символ
«арксинус трёх пятых»

С помощью введённого символа можно записать корни

Решим уравнение
С помощью числовой окружности получим решение.

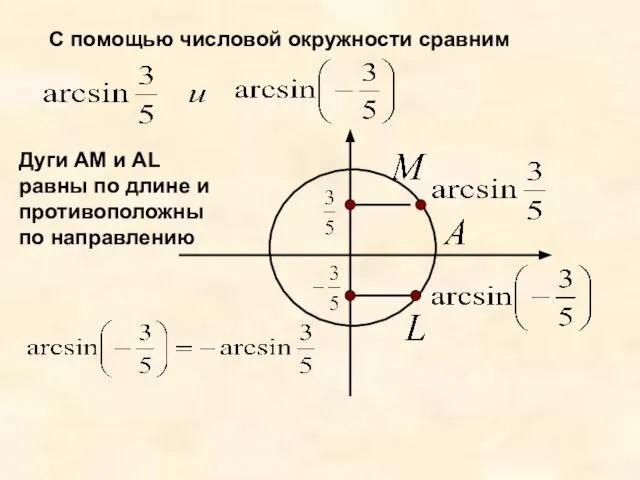
С помощью числовой окружности сравним
Дуги AM и AL равны по длине и противоположны по направлению

Получим

Определение

Существует три частных случая решения уравнения sin t = a

Пример 1.
Вычислить:

Пример 1.
Вычислить:

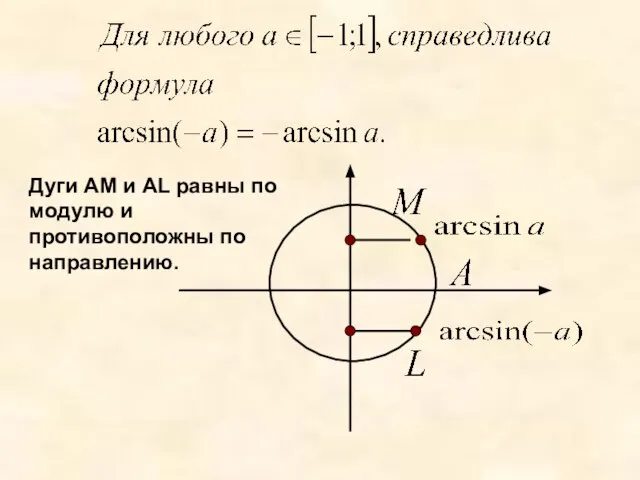
Дуги АМ и АL равны по модулю и противоположны по направлению.

Пример 2.
Решить уравнение

Пример 2.
Решить уравнение

Пример 2.
Решить уравнение

Принята общая формула решения тригонометрического уравнения sin t = a

Пример 3.
Решить неравенство
Строим окружность
Учитываем, что синус – это ордината точки числовой окружности.
P
M
Следовательно
Данному неравенству соответствуют точки открытой дуги MP
Получим

Решите из учебника
№ 16.1, 16.3, 16.5, 16.9, 16.11

Задание на дом
§ 16 выучить
№ 16.2, 16.4, 16.6