Безмасштабные сети(scale-free networks)

Граф
Граф или неориентированный граф G — это упорядоченная пара G: = (V,E), для которой выполнены следующие условия:
V это множество вершин или узлов,
E это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

Диаметр графа — это максимум расстояния между вершинами для всех пар вершин. Расстояние между вершинами — наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую.

Граф называется связным, если любые две несовпадающие вершины графа соединены маршрутом. Очевидно, что для связности графа необходимо и достаточно, чтобы произвольная фиксированная вершина графа соединялась маршрутом с каждой из оставшихся вершин этого графа.

Числом реберной связности графа называется число, равное наименьшему числу ребер, удаление которых приводит к несвязному графу. Число реберной связности одновершинного графа полагается равным нулю

Числом вершинной связности (или просто числом связности) графа называется число, равное наименьшему числу вершин, удаление которых приводит к несвязному или одновершинному графу

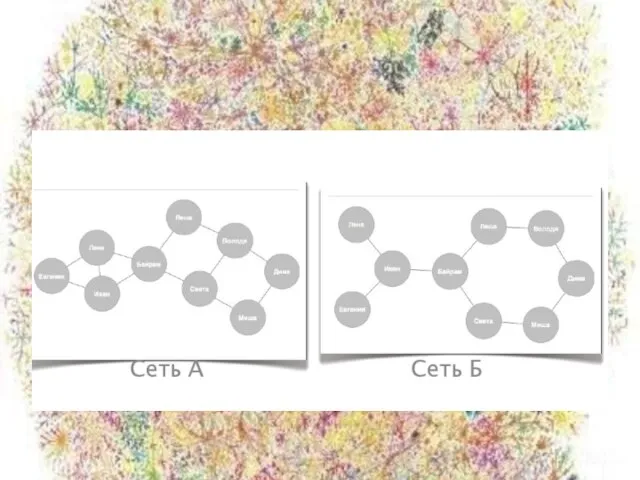
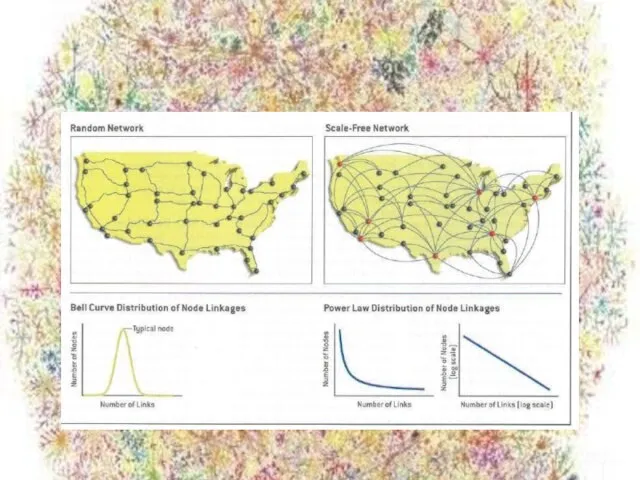
Две категории сетей
Классические(случайные) - новые узлы присоединяются к существующим примерно с одинаковой вероятностью,
Безмасштабные - существуют узлы притягивающие непропорционально большое число новых узлов (концентраторы)
Пример классической сети
Пример безмасштабной сети

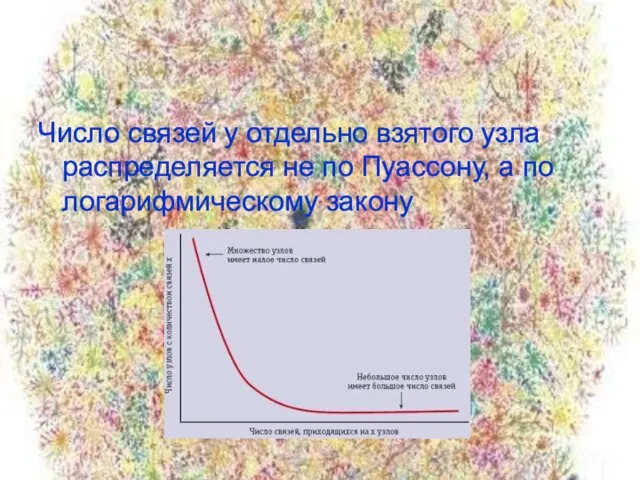
Число связей у отдельно взятого узла распределяется не по Пуассону, а по логарифмическому закону. Отсюда следует, что в большинстве реальных сетей основная часть узлов имеет ограниченное число связей, а отдельные узлы-концентраторы (Барабаши называет их hub) имеют аномально большое число связей

Число связей у отдельно взятого узла распределяется не по Пуассону, а по логарифмическому закону

Где мы можем увидеть безмасштабные сети?
Техника: Сети электропередачи, Интернет, Веб, ...
Социум: половые контакты, связи, организации, дороги, авиамаршруты ...
Биология: нейроны; пищевые, экологические, метаболические сети, ...
Физика: молекулы, галактики…

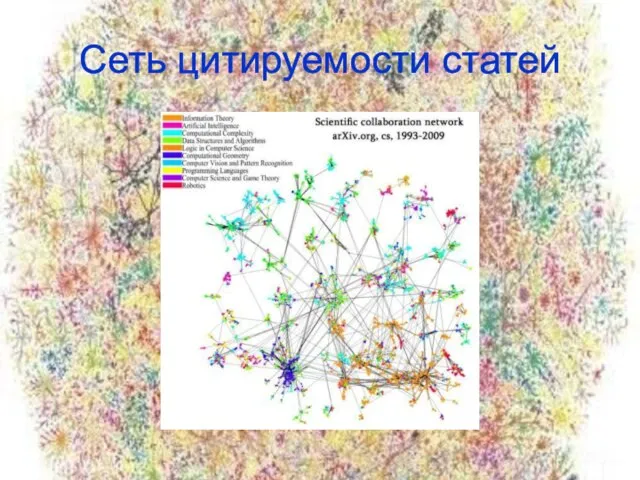
Сеть цитируемости статей

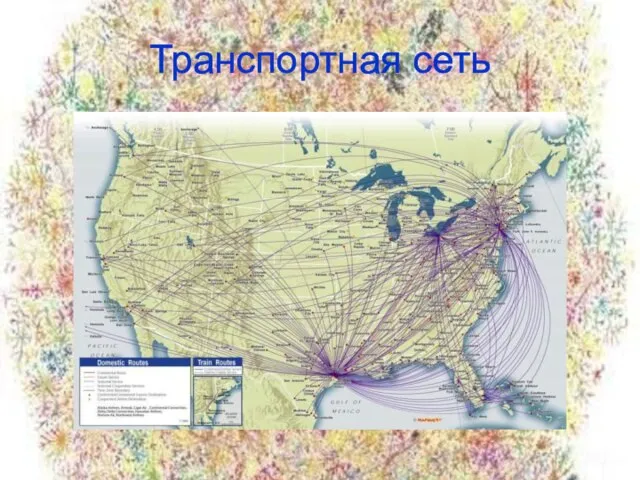
Транспортная сеть

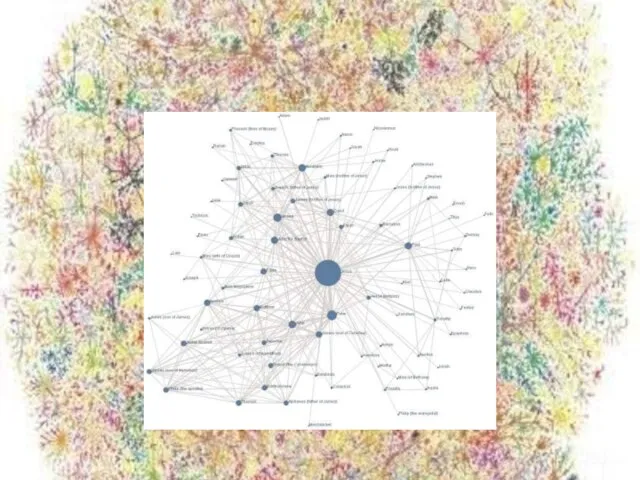
Социальная сеть

Human Sexual Contacts

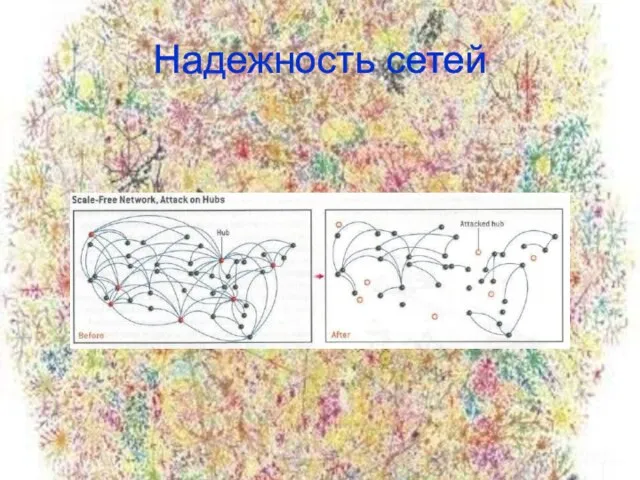
Надежность сетей
При удалении некоторого процента узлов, скажем 5%, граф рассыпается на мелкие кусочки, гигантский кластер перестаёт существовать
Рост безмасштабной сети не приводит к увеличению ее устойчивости к случайным воздействиям

Надежность сетей

Надежность сетей

Надежность сетей

Вирусология
Лечить случайные узлы ни к чему не
приводит
Если лечить хабы, то можно быстро
погасить эпидемию
СПИД, компьютерные вирусы

Предсказание
Кто с кем напишет следующую статью?
Где проложат новые дороги?
Кто присоединится к группе риска?

СУБД
Кластеризация: запросы к сетям будут
бегать по соседям.
Что делать с хабами? С костяком?
Зависит от кластеризации или s-метрики.