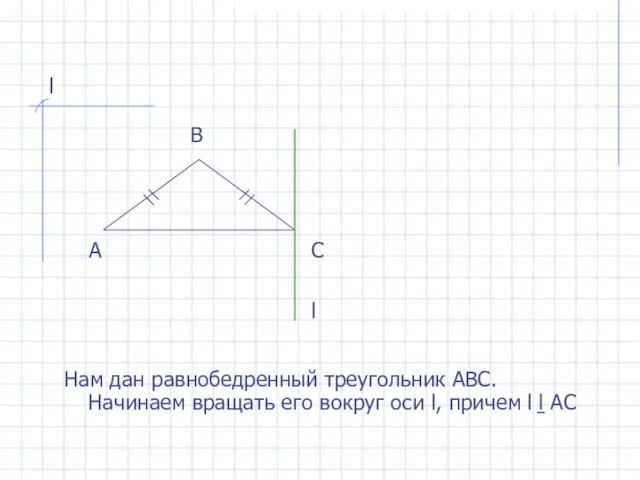
C 18 № 2

l
Нам дан равнобедренный треугольник АВС. Начинаем вращать его вокруг оси l, причем l ḻ АС
l
A
B
C

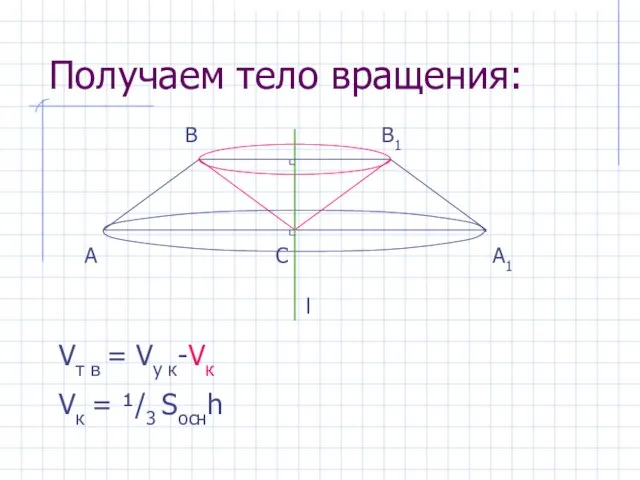
Получаем тело вращения:
А
А1
Vт в = Vу к-Vк
Vк = ¹/3 Sоснh
В
В1
С
l

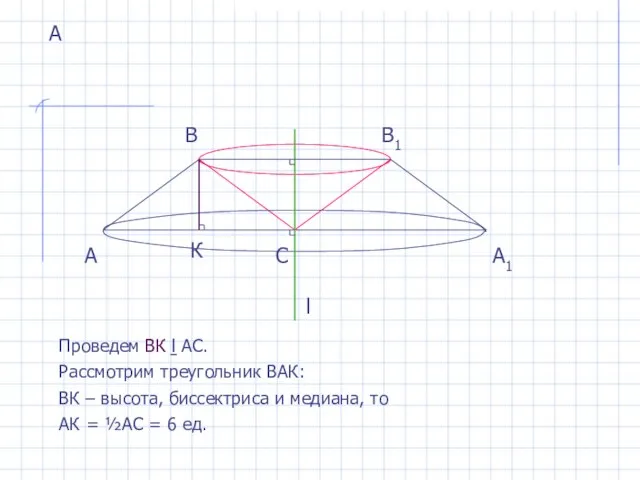
А
А
А1
Проведем ВК ḻ АС.
Рассмотрим треугольник ВАК:
ВК – высота, биссектриса и медиана, то
АК = ½АС = 6 ед.
В
В1
С
l
К

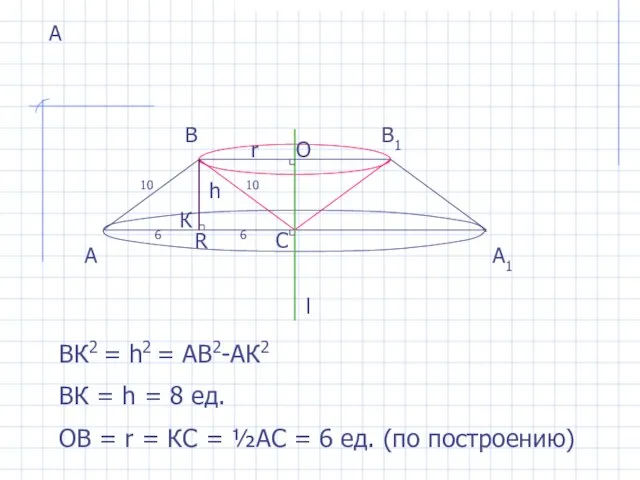
А
А
А1
ВК2 = h2 = AB2-АК2
ВК = h = 8 ед.
ОВ = r = КС = ½АС = 6 ед. (по построению)
В
В1
С
l
К
h
R
r
О
6
10
10
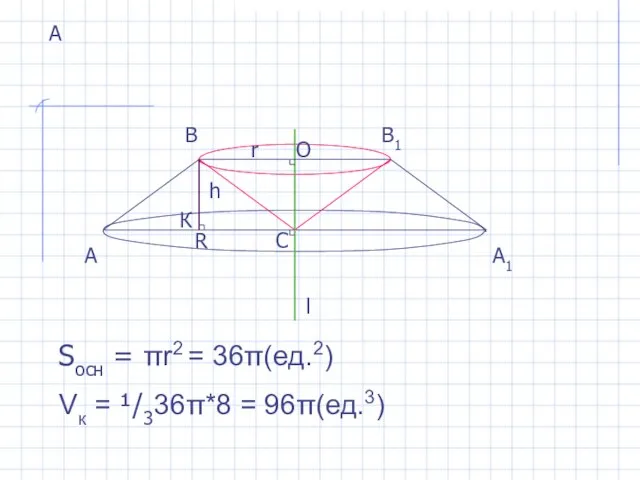
6

А
А
А1
Sосн = πr2 = 36π(ед.2)
Vк = ¹/336π*8 = 96π(ед.3)
В
В1
С
l
К
h
R
r
О

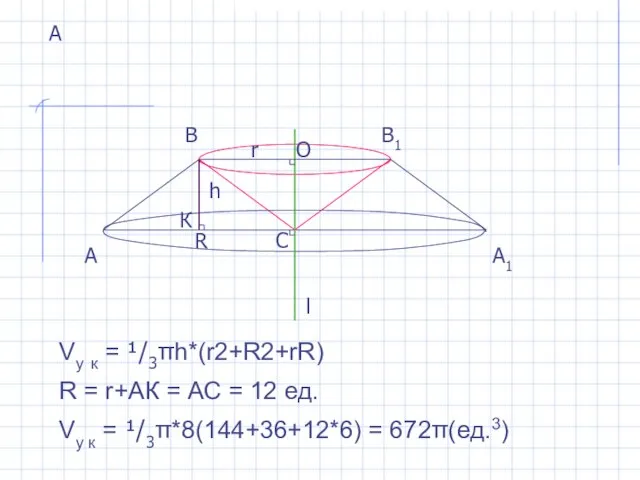
А
А
А1
Vу к = ¹/3πh*(r2+R2+rR)
R = r+AК = АС = 12 ед.
Vу к = ¹/3π*8(144+36+12*6) = 672π(ед.3)
В
В1
С
l
К
h
R
r
О

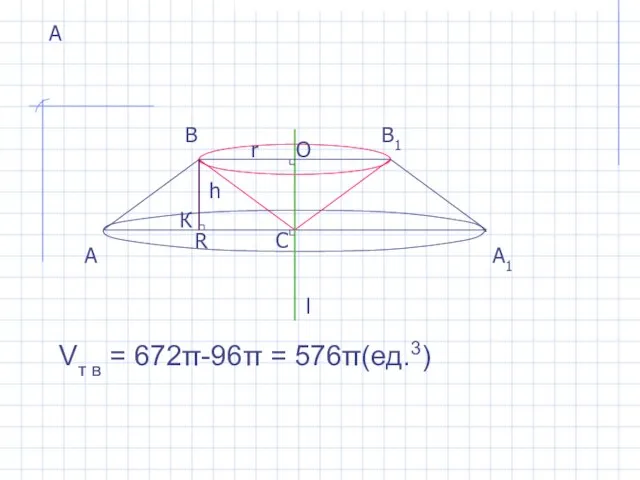
А
А
А1
Vт в = 672π-96π = 576π(ед.3)
В
В1
С
l
К
h
R
r
О