Содержание
- 2. Наряду с расчетом конструкций компьютерное моделирование и симуляция могут использоваться и для оптимизации проектов. Оптимизацию можно
- 3. Метод конечных элементов (МКЭ, Finite Elements Method, FEM) наиболее распространенный численный метод решения задач прикладной механики,
- 4. Схема перехода от твердотельной модели к расчетной сетке Современные системы автоматизации инженерных расчетов, как правило, применяются
- 5. Расчетные системы позволяют «заглянуть» внутрь детали, что практически невозможно при натурных прочностных испытаниях, получить исчерпывающую картину
- 6. Анализ напряженно-деформированного состояния детали в системе ANSYS Моделирование аварийного удара автомобиля
- 7. Моделирование кинематики Пространственные механизмы являются важной составляющей современной техники и производственных технологий, например шасси самолетов и
- 8. Моделирование прямой задачи кинематики в CATIA Решение обратной задачи кинематики в КОМПАС 3D
- 9. Еще одной важной задачей, решаемой в кинематических расчетных системах, является определение работоспособности механизмов: отсутствие заклиниваний; предупреждение
- 10. Аэрогидродинамические расчеты Вычислительная гидрогазодинамика (CFD, Computational Fluid Dynamics) широко при-меняется как в традиционных для нее отраслях:
- 11. Расчет течения в вихревом насосе Расчетная сетка для моделирования обтекания антикрыла гоночного автомобиля
- 12. В ряде случаев даже наличие геометрической симметрии в модели не позволяет рассматривать половину модели ввиду несимметричности
- 13. Другим примером использования CFD для создания бытовых продуктов можно назвать моделирование течений в водопроводных и канализационных
- 15. Скачать презентацию
Слайд 2 Наряду с расчетом конструкций компьютерное моделирование и симуляция могут использоваться и для
Наряду с расчетом конструкций компьютерное моделирование и симуляция могут использоваться и для

Таким образом, численное моделирование задач прочности существенно экономит время, ресурсы, позволяет сократить объемы натурных испытаний, а также более тщательно оптимизировать конструкции.
Слайд 3 Метод конечных элементов (МКЭ, Finite Elements Method, FEM) наиболее распространенный численный метод
Метод конечных элементов (МКЭ, Finite Elements Method, FEM) наиболее распространенный численный метод

Метод конечных элементов
Слайд 4Схема перехода от твердотельной модели к расчетной сетке
Современные системы автоматизации инженерных расчетов,
Схема перехода от твердотельной модели к расчетной сетке
Современные системы автоматизации инженерных расчетов,

Существенным достоинством расчетных систем перед проверочными натурными испытаниями является возможность определения элементов не только с недостаточной прочностью, но и с избыточной. Это позволяет оптимизировать геометрию деталей с целью снижения их массы, что особенно критично, например, в авиакосмической отрасли, двигателестроении.
Слайд 5 Расчетные системы позволяют «заглянуть» внутрь детали, что практически невозможно при натурных прочностных
Расчетные системы позволяют «заглянуть» внутрь детали, что практически невозможно при натурных прочностных

Современные расчетные системы обеспечивают:
комплексный анализ характеристик конструкций, включая расчет напряженно-деформированного состояния, собственных частот и форм колебаний;
анализ устойчивости;
решение задач теплопередачи;
исследование установившихся и неустановившихся процессов;
исследование акустических явлений;
исследование нелинейных статических процессов;
исследование нелинейных динамических переходных процессов;
расчет критических частот и вибраций роторных машин;
анализ частотных характеристик при воздействии случайных нагрузок.
Предусмотрена возможность моделирования практически всех типов материалов, включая композитные и эластичные.
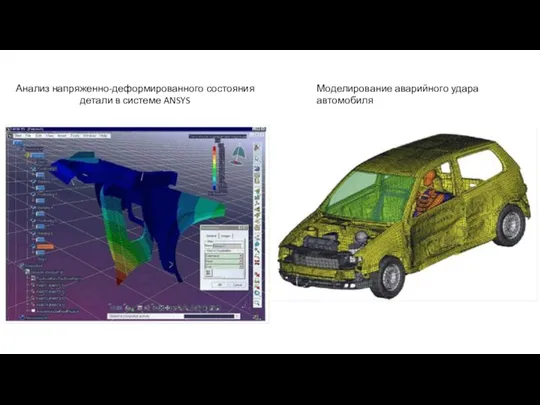
Слайд 6Анализ напряженно-деформированного состояния детали в системе ANSYS
Моделирование аварийного удара автомобиля
Анализ напряженно-деформированного состояния детали в системе ANSYS
Моделирование аварийного удара автомобиля
Слайд 7Моделирование кинематики
Пространственные механизмы являются важной составляющей современной техники и производственных технологий, например
Моделирование кинематики
Пространственные механизмы являются важной составляющей современной техники и производственных технологий, например

Так как конструирование сложных механизмов осуществляется с использованием MCAD-систем, то логичным стало использование полученных геометрических моделей для моделирования и анализа их движения. Проектирование кинематики отличается высокой геометрической сложностью и в существенной степени определяет качество конечного продукта, стоимость его изготовления и эксплуатации.
В 70-80-е годы, в период активного развития рабочих станций и их применения для проектирования изделий машиностроения, появились первые системы для динамического и кинематического анализа пространственных механизмов, такие как ADAMS, ANSYS Mechanical, COSMOS Motion и др. К настоящему времени эти системы получили признание специалистов и вошли в повседневную практику работы сотен тысяч инженеров.
Инженерные системы моделирования кинематики обеспечивают возможность решения как прямых, так и обратных задач. Прямая задача заключается в том, чтобы по известным усилиям и другим характеристикам приводов (пневмо- и гидроцилиндров, электродвигателей и т. п.) определить скорости и траектории движения всех элементов, составляющих механизм. При решении обратной (часто употребляется термин инверсная) задачи - напротив: по известной или заданной траектории и скорости перемещения одного из звеньев (как правило, конечного) требуется определить траектории остальных звеньев, силы, действующие на них, и, соответственно, требуемые силовые и скоростные характеристики приводов.
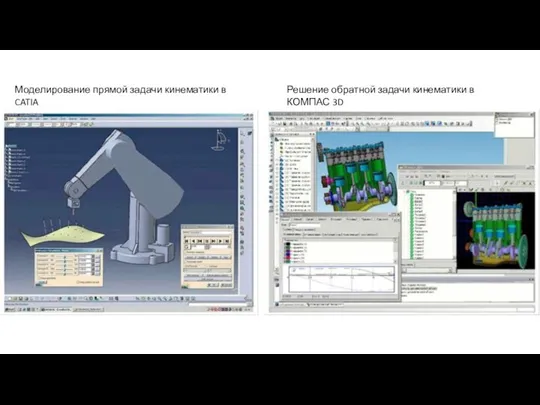
Слайд 8Моделирование прямой задачи кинематики в CATIA
Решение обратной задачи кинематики в КОМПАС 3D
Моделирование прямой задачи кинематики в CATIA
Решение обратной задачи кинематики в КОМПАС 3D
Слайд 9 Еще одной важной задачей, решаемой в кинематических расчетных системах, является определение работоспособности
Еще одной важной задачей, решаемой в кинематических расчетных системах, является определение работоспособности
отсутствие заклиниваний;
предупреждение нежелательных касаний и столкновений элементов механизма;
вписывание механизма в заданные габариты.
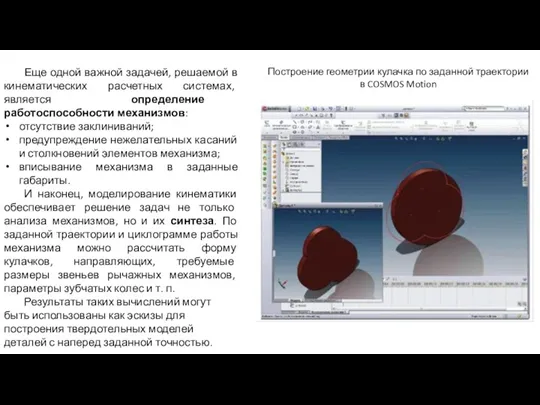
И наконец, моделирование кинематики обеспечивает решение задач не только анализа механизмов, но и их синтеза. По заданной траектории и циклограмме работы механизма можно рассчитать форму кулачков, направляющих, требуемые размеры звеньев рычажных механизмов, параметры зубчатых колес и т. п.
Результаты таких вычислений могут быть использованы как эскизы для построения твердотельных моделей деталей с наперед заданной точностью.
Построение геометрии кулачка по заданной траектории в COSMOS Motion
Слайд 10Аэрогидродинамические расчеты
Вычислительная гидрогазодинамика (CFD, Computational Fluid Dynamics) широко при-меняется как в традиционных
Аэрогидродинамические расчеты
Вычислительная гидрогазодинамика (CFD, Computational Fluid Dynamics) широко при-меняется как в традиционных

Расчеты осуществляются с использованием численных методов и алгоритмов для решения и анализа задач течений жидкостей и газов, как правило, состоящих в решении уравнений Навье-Стокса методами конечных объемов, конечных элементов, конечных разностей и др. Современные программные комплексы для моделирования течений в жидкости и газах позволяют рассчитывать широкий диапазон течений по числу Маха, многофазные и много-компонентные течения, течения в несжимаемых жидкостях.
При рассмотрении актуальных промышленных задач расчетная модель должна обеспечивать точную передачу геометрии без упрощений, характерных для задач расчета напряженно-деформированного состояния.
Слайд 11Расчет течения в вихревом насосе
Расчетная сетка для моделирования обтекания антикрыла гоночного автомобиля
Расчет течения в вихревом насосе
Расчетная сетка для моделирования обтекания антикрыла гоночного автомобиля

Слайд 12 В ряде случаев даже наличие геометрической симметрии в модели не позволяет
В ряде случаев даже наличие геометрической симметрии в модели не позволяет

Первоначально вычислительная гидроаэродинамика использовалась применительно к задачам проектирования авиационной, космической техники и судостроения. С развитием программных средств и повышением производительности настольных ПК она находит все более широкое применение и в других отраслях. Некоторые, ставшие привычными продукты было бы очень трудно спроектировать без ее использования, например струйные принтеры. Использование CFD при проектировании струйных принтеров оправдано и дает ряд преимуществ для изучения того, как форма, размер и скорость испускаемой капли зависят от таких параметров, как импульс управляющего давления, форма форсунки, коэффициент поверхностного натяжения, и многое другое.
Моделирование образования капли в струйном принтере
Слайд 13 Другим примером использования CFD для создания бытовых продуктов можно назвать моделирование течений
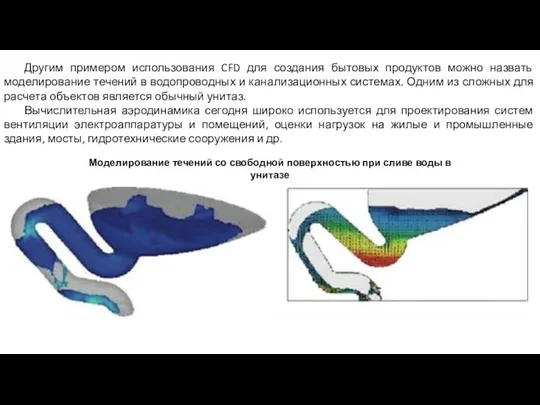
Другим примером использования CFD для создания бытовых продуктов можно назвать моделирование течений
Вычислительная аэродинамика сегодня широко используется для проектирования систем вентиляции электроаппаратуры и помещений, оценки нагрузок на жилые и промышленные здания, мосты, гидротехнические сооружения и др.
Моделирование течений со свободной поверхностью при сливе воды в унитазе
 Бронза
Бронза В моей презентации представлены эскизы вечерних платьев, выполненные в графическом редакторе «Adobe Photoshop». Эти эскизы- мое личное тв
В моей презентации представлены эскизы вечерних платьев, выполненные в графическом редакторе «Adobe Photoshop». Эти эскизы- мое личное тв СПК Ольшанка
СПК Ольшанка Человек имеет право
Человек имеет право Week 1. Lesson 1
Week 1. Lesson 1 Стресс-менеджмент руководителя
Стресс-менеджмент руководителя «Как помочь птицам»
«Как помочь птицам» Образование и наука
Образование и наука История натуральных чисел
История натуральных чисел Презентация на тему РАВНОМЕРНОЕ ДВИЖЕНИЕ Механическое движение: перемещение, скорость, ускорение
Презентация на тему РАВНОМЕРНОЕ ДВИЖЕНИЕ Механическое движение: перемещение, скорость, ускорение  Мутации
Мутации Эпический театр Бертольта Брехта
Эпический театр Бертольта Брехта Всё о кино
Всё о кино Консультация по проведению артикуляционной гимнастики.(для родителей)
Консультация по проведению артикуляционной гимнастики.(для родителей) Как контролировать интенсивность физической нагрузки
Как контролировать интенсивность физической нагрузки Предметы домашней утвари в русской избе
Предметы домашней утвари в русской избе Отчет отряда "Факел" за 2009-2010 уч.г.
Отчет отряда "Факел" за 2009-2010 уч.г. Все работы хороши, выбирай на вкус
Все работы хороши, выбирай на вкус Общие сведения о Банке АБ «ИНТЕРПРОГРЕССБАНК» (ЗАО) – универсальный кредитно-финансовый институт, приоритетным направлением деят
Общие сведения о Банке АБ «ИНТЕРПРОГРЕССБАНК» (ЗАО) – универсальный кредитно-финансовый институт, приоритетным направлением деят Бар-ресторан Штольня
Бар-ресторан Штольня ЗАГАЛЬНІ ЗАКОНОМІРНОСТІ ГОРІННЯ ГАЗОПОВІТРЯНИХ СИСТЕМ
ЗАГАЛЬНІ ЗАКОНОМІРНОСТІ ГОРІННЯ ГАЗОПОВІТРЯНИХ СИСТЕМ Курс на импортозамещение – долгосрочный приоритет
Курс на импортозамещение – долгосрочный приоритет Электронный инструментарий реализации модели управления развитием системы оценки качества образования на уровне ОУ
Электронный инструментарий реализации модели управления развитием системы оценки качества образования на уровне ОУ Сегментирование потребителей
Сегментирование потребителей Колледж железнодорожной медицины
Колледж железнодорожной медицины java. lang (Java Language) Package
java. lang (Java Language) Package Каноническое право Пацков Артём Юб02/1402
Каноническое право Пацков Артём Юб02/1402 Нужно ли запрещать мат
Нужно ли запрещать мат