Центральная и осевая симметрии

Рассмотреть осевую и центральную симметрии как свойства некоторых геометрических фигур;
Уметь строить симметричные точки и уметь распознавать фигуры, являющиеся симметричными относительно точки или прямой;
Совершенствование навыков решения задач;
Продолжить работу над аккуратностью записи и выполнения геометрического чертежа;
Цели урока:

Устная работа
«Щадящий опрос»
Какая точка называется серединой отрезка?
Какой треугольник называется равнобедренным?
Каким свойством обладают диагонали ромба?
Сформулируйте свойство биссектрисы равнобедренного треугольника.
Какие прямые называются перпендикулярными?
Какой треугольник называется равносторонним?
Каким свойством обладают диагонали квадрата?
Какие фигуры называются равными?

А
Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему
А
А1
а
О
а – ось симметрии

Являются ли данные точки симметричными ?
М
М1
m
С
D
b
B
В1
а
Рисунок 1
Рисунок 2
Рисунок 3

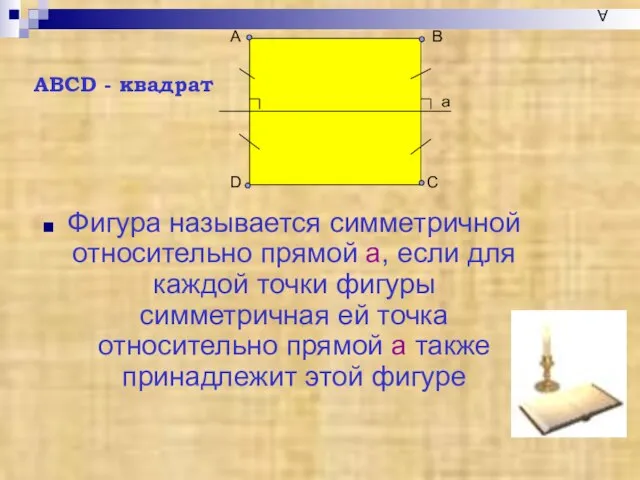
А
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре
А
В
С
D
а
АВСD - квадрат

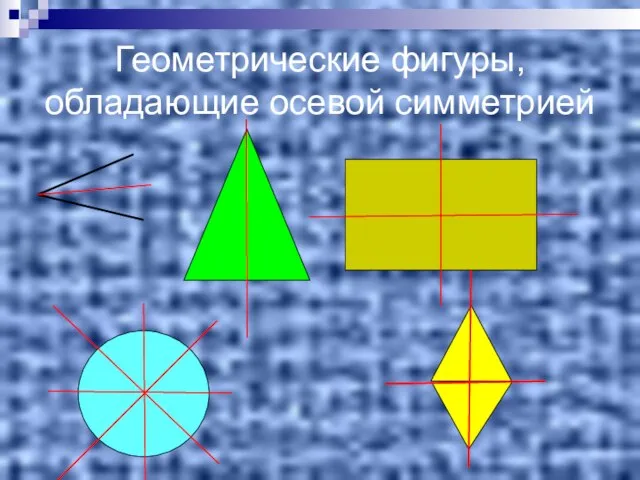
Геометрические фигуры, обладающие осевой симметрией

Фигуры, обладающие осевой симметрией

А
Сколько осей симметрии имеет:
Отрезок
Прямая
Луч
А
В
а
О
Е
одна
множество
Ни одной
Задачи:

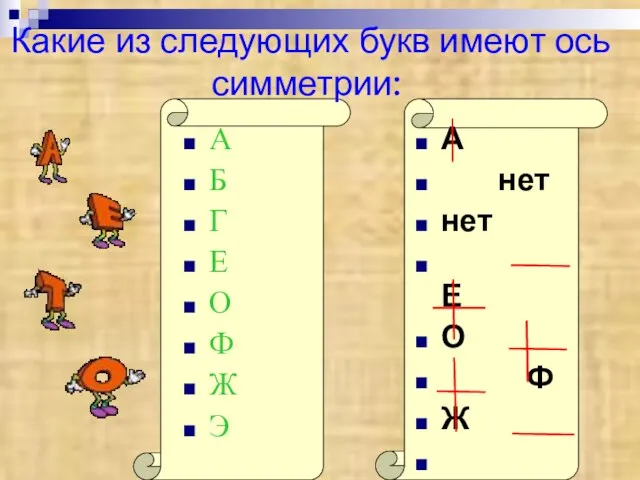
Какие из следующих букв имеют ось симметрии:
А
Б
Г
Е
О
Ф
Ж
Э
А
нет
нет
Е
О
Ф
Ж
Э

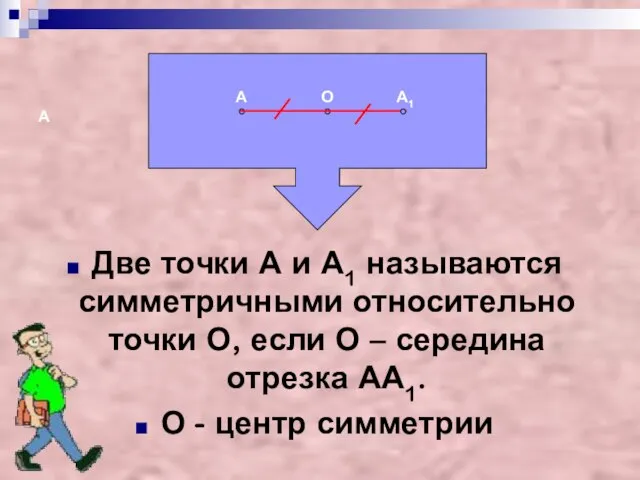
А
Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.
О - центр симметрии
А
О
А1

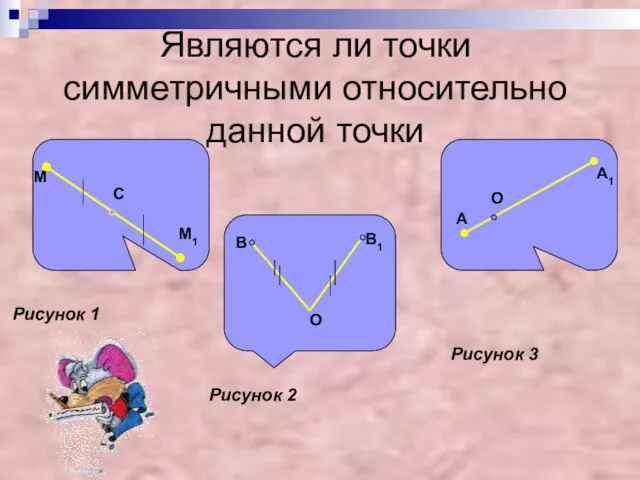
Являются ли точки симметричными относительно данной точки
Рисунок 1
Рисунок 2
Рисунок 3
М1
В
В1
О
М
А
А1
О
С

А
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно О также принадлежит этой фигуре.
О – центр симметрии квадрата
А
В
С
Д
О

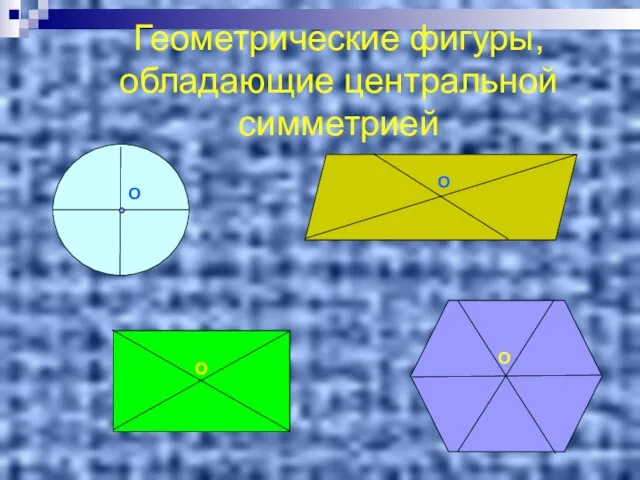
Геометрические фигуры, обладающие центральной симметрией
О
О
О
О

Фигуры, обладающие центральной симметрией

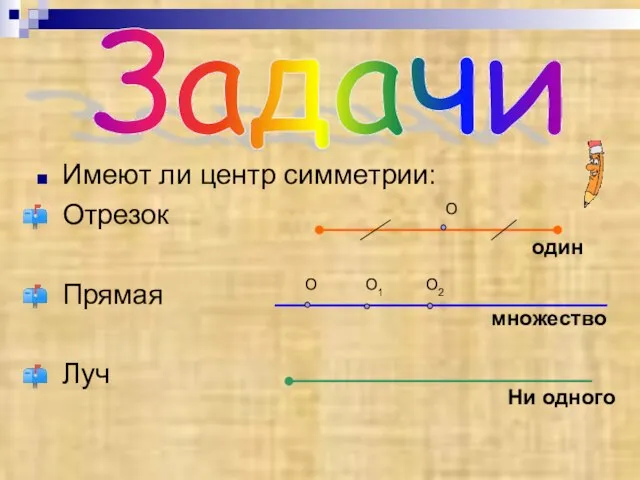
О
Имеют ли центр симметрии:
Отрезок
Прямая
Луч
Задачи
О
один
множество
Ни одного
О
О1
О2

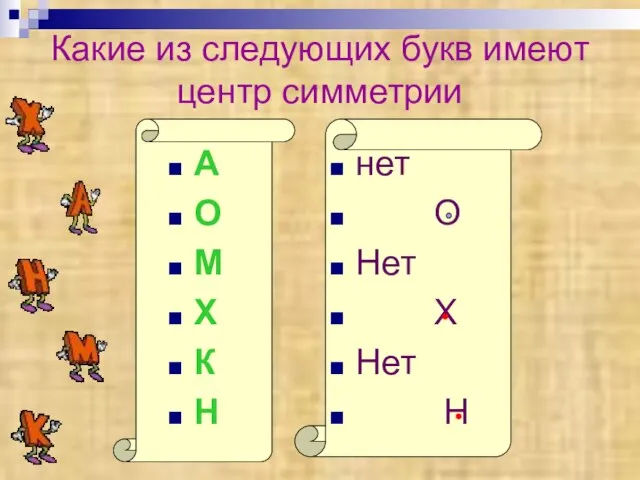
Какие из следующих букв имеют центр симметрии
А
О
М
Х
К
Н
нет
О
Нет
Х
Нет
Н