Четыре замечательные точки треугольника

Из истории

ИЗ ИСТОРИИ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКА
В четвертой книге "Начал" Евклид решает задачу: "Вписать круг в данный треугольник". Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга. Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга. В "Началах" не говорится о том, что и три высоты треугольника пересекаются в одной точке, называемой ортоцентром (греческое слово "ортос" означает "прямой", "правильный"). Это предложение было, однако, известно Архимеду, Паппу, Проклу. Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника.
На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы "замечательными" или "особенными" точками треугольника. Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – "геометрии треугольника" или "новой геометрии треугольника", одним из родоначальников которой стал Леонард Эйлер.
В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже "прямой Эйлера". В двадцатых годах XIX века французские математики Ж. Понселе, Ш. Брианшон и другие установили независимо друг от друга следующую теорему: основания медиан, основания высот и середины отрезков высот, соединяющих ортоцентр с вершинами треугольника, лежат на одной и той же окружности.
Эта окружность называется "окружностью девяти точек", или "окружностью Фейербаха", или "окружностью Эйлера". К. Фейербах установил, что центр этой окружности лежит на прямой Эйлера.
Большой вклад в развитие геометрии треугольника внесли математики XIX – XX веков Лемуан, Брокар, Тебо и другие.

План урока
Теорема о медианах треугольника
Свойство биссектрисы угла
Свойство серединного перпендикуляра к отрезку
Теорема о биссектрисах треугольника
Теорема о серединных перпендикулярах к сторонам треугольника
Теорема о высотах треугольника
Контрольные вопросы

Теорема о медианах треугольника
Th Медианы тр-ка пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
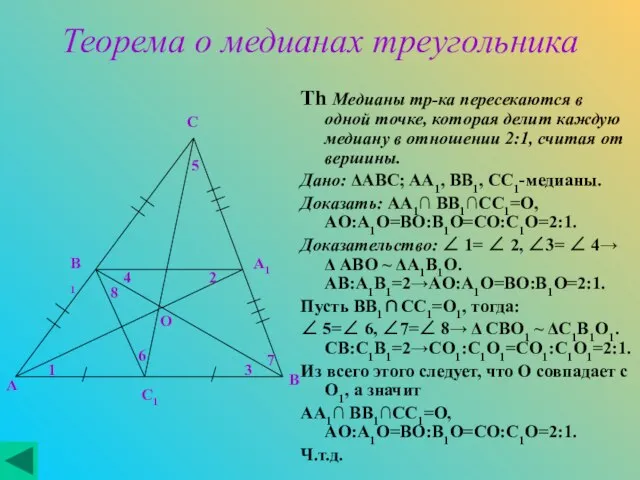
Дано: ΔABC; AA1, BB1, CC1-медианы.
Доказать: AA1∩ BB1∩CC1=O, AO:A1O=BO:B1O=CO:C1O=2:1.
Доказательство: ∠ 1= ∠ 2, ∠3= ∠ 4→ Δ ABO ~ ΔA1B1O. AB:A1B1=2→AO:A1O=BO:B1O=2:1.
Пусть BB1∩CC1=O1, тогда:
∠ 5=∠ 6, ∠7=∠ 8→ Δ CBO1 ~ ΔC1B1O1. CB:C1B1=2→CO1:C1O1=CO1:C1O1=2:1.
Из всего этого следует, что O совпадает с O1, а значит
AA1∩ BB1∩CC1=O, AO:A1O=BO:B1O=CO:C1O=2:1.
Ч.т.д.

Свойство биссектрисы углы
Th Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
Дано: ∠BAC; AM – биссектриса (∠1=∠2);
KM-перпендикуляр к AB; ML-перпендикуляр к AC.
Доказать: KM=KL.
Доказательство: AM – общая гипотенуза, ∠1=∠2 → ΔAKM=Δ ALM по гипотенузе и острому углу → KM=KL. Ч.т.д.
Th Каждая точка, лежащая внутри неразвернутого угла и равноудаленная от его сторон, лежит на биссектрисе этого угла.
Дано: ∠BAC; KM-перпендикуляр к AB; ML-перпендикуляр к AC; KM=KL.
Доказать: AM – биссектриса ∠BAC.
Доказательство: AM – общая гипотенуза, KM=KL → ΔAKM=Δ ALM по гипотенузе и катету → ∠1=∠2, то есть AM – биссектриса ∠BAC . Ч.т.д.
A
B
C
K
L
M
1
2

Свойство серединного перпендикуляра к отрезку
O Серединный перпендикуляр-прямая, проходящая через середину отрезка и перпендикулярная к нему.
Th Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Дано:O-середина AB, m–серединный перпендикуляр к AB, M принадлежит m.
Доказать: AM=MB.
Доказательство: 1)Если M совпадает с O, то AM=MB=AO=BO. Ч.т.д.
2)AO=OB – катеты, MO – общий катет→
ΔAMO=ΔBMO-по двум катетам→AM=MB. Ч.т.д.
Th Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Дано:O-середина AB, m–серединный перпендикуляр к AB, AM=MB.
Доказать: M принадлежит m.
Доказательство: 1)Если M лежит на AB, то AM=MB=AO=BO, и M принадлежит m. Ч.т.д.
2)AM=MB→ ΔAMB-равнобедренный→MO-медиана и высота ΔAMB→MO совпадает с m, и M принадлежит m. Ч.т.д.

Теорема о биссектрисах треугольника
Th Биссектрисы треугольника пересекаются в одной точке.
Дано: ΔABC, AA1, BB1, CC1 – биссектрисы ΔABC.
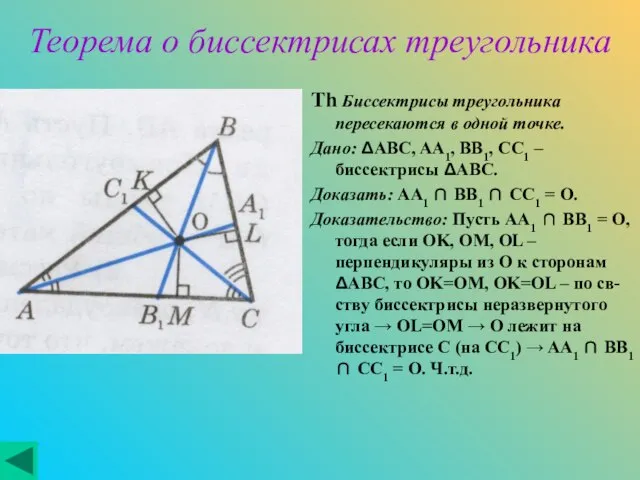
Доказать: AA1 ∩ BB1 ∩ CC1 = O.
Доказательство: Пусть AA1 ∩ BB1 = O, тогда если OK, OM, OL – перпендикуляры из O к сторонам ΔABC, то OK=OM, OK=OL – по св-ству биссектрисы неразвернутого угла → OL=OM → O лежит на биссектрисе С (на СС1) → AA1 ∩ BB1 ∩ CC1 = O. Ч.т.д.

Теорема о серединных перпендикулярах к сторонам треугольника
Th Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Дано: ΔABC, m-серединный п-р к AB, n-серединный п-р к BC, p-серединный перпендикуляр к AC.
Доказать:m∩n∩p = O.
Доказательство: m∩n O, т.к. если m параллельна n, то m перпендикулярна BC, и через B проходят 2 прямые AB, BC, перпендикулярные к m, чего не может быть.
По св-ству серединного перпендикуляра к отрезку, OA=OB, OB=OC → OA=OC →
O лежит на серединном перпендикуляре к AC, т.е. на p → m∩n∩p=O. Ч.т.д.

Теорема о высотах треугольника
Th Прямые, на которых лежат высоты треугольника, пересекаются в одной точке.
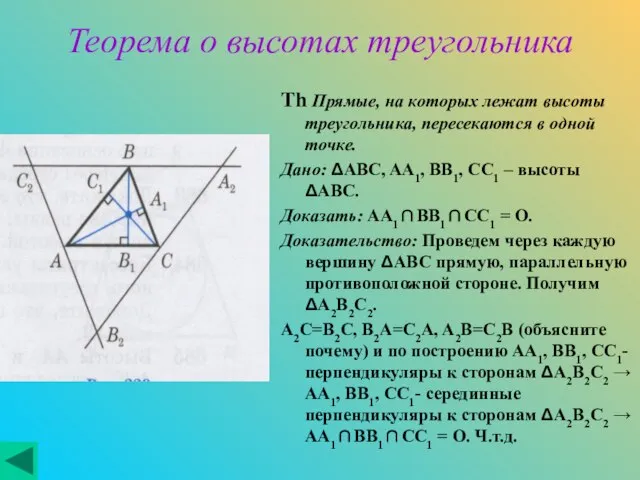
Дано: ΔABC, AA1, BB1, CC1 – высоты ΔABC.
Доказать: AA1∩BB1∩CC1 = O.
Доказательство: Проведем через каждую вершину ΔABC прямую, параллельную противоположной стороне. Получим ΔA2B2C2.
A2C=B2C, B2A=C2A, A2B=C2B (объясните почему) и по построению AA1, BB1, CC1- перпендикуляры к сторонам ΔA2B2C2 → AA1, BB1, CC1- серединные перпендикуляры к сторонам ΔA2B2C2 → AA1∩BB1∩CC1 = O. Ч.т.д.