Чевианы треугольникаСвойства медиан

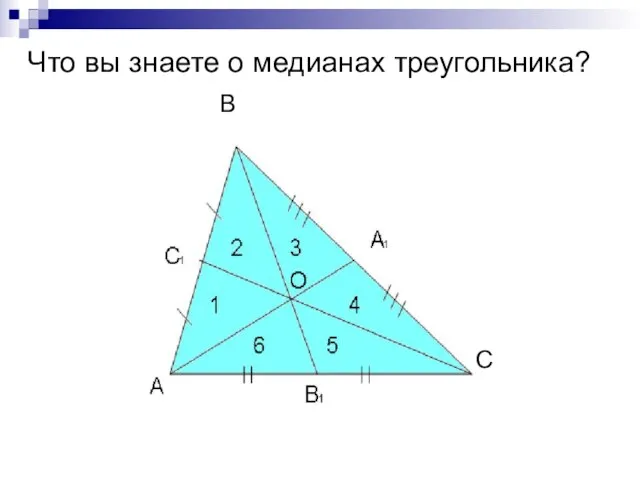
С
В
Что вы знаете о медианах треугольника?

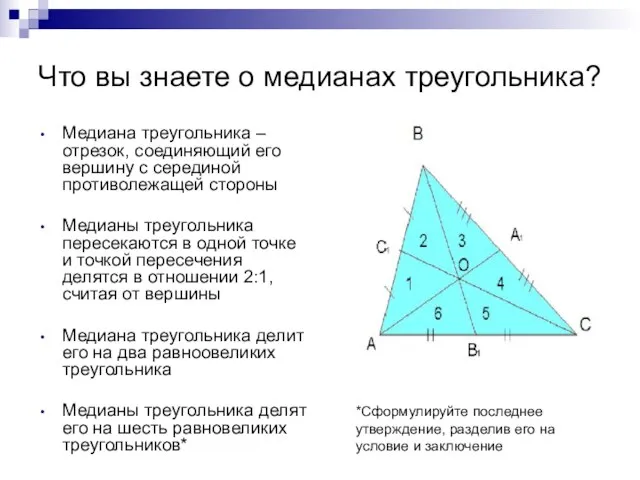
Что вы знаете о медианах треугольника?
Медиана треугольника – отрезок, соединяющий его вершину с серединой противолежащей стороны
Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины
Медиана треугольника делит его на два равноовеликих треугольника
Медианы треугольника делят его на шесть равновеликих треугольников*
*Сформулируйте последнее утверждение, разделив его на условие и заключение

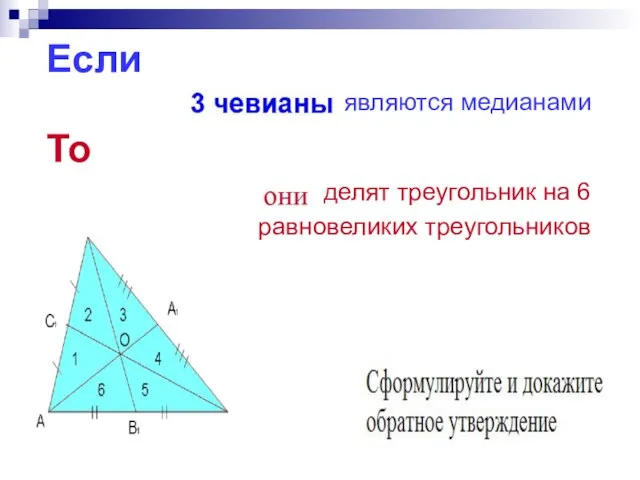
Если
являются медианами
То
делят треугольник на 6
равновеликих треугольников

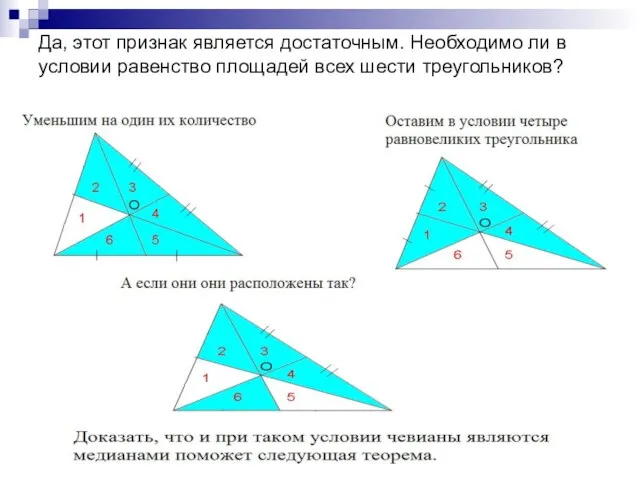
Да, этот признак является достаточным. Необходимо ли в условии равенство площадей всех шести треугольников?

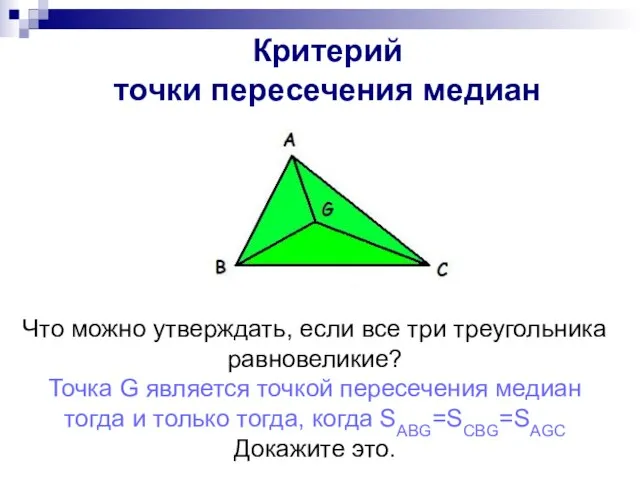
Критерий точки медианы

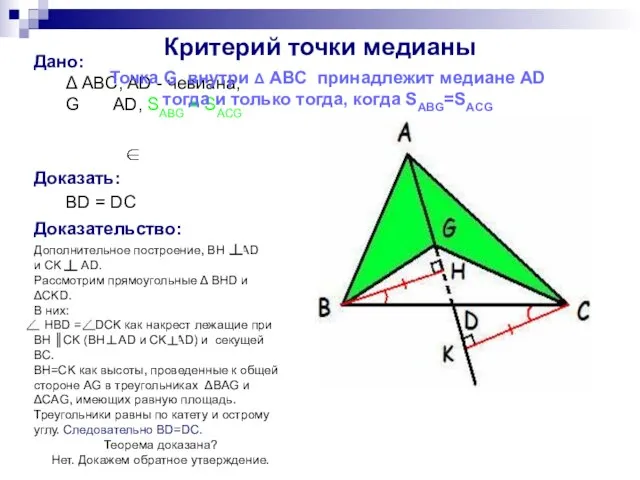
Дано:
Δ ABC, AD - чевиана,
G AD, SABG = SACG
Критерий точки медианы
Точка G внутри Δ АВС принадлежит медиане AD
тогда и только тогда, когда SABG=SACG
Доказать:
BD = DC
Доказательство:
Дополнительное построение, BH AD и CK AD.
Рассмотрим прямоугольные Δ BHD и ΔСKD.
В них:
НBD = DCK как накрест лежащие при BH ║CK (BH AD и CK AD) и секущей BC.
ВH=CK как высоты, проведенные к общей стороне AG в треугольниках ΔBAG и ΔCAG, имеющих равную площадь.
Треугольники равны по катету и острому углу. Следовательно BD=DC.
Теорема доказана?
Нет. Докажем обратное утверждение.

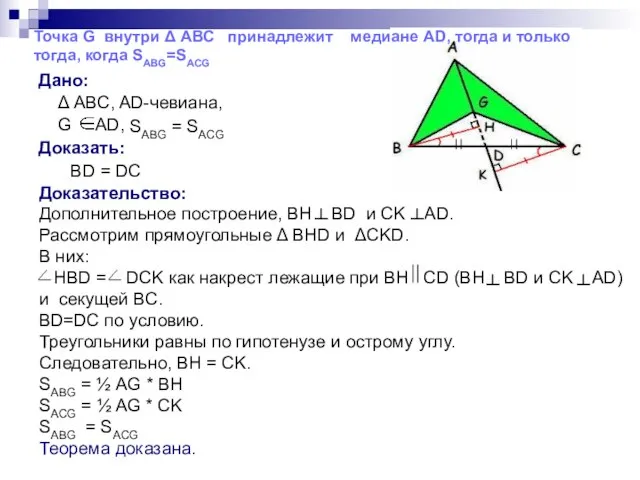
Дано:
Δ ABC, AD-чевиана,
G AD,
Доказать:
BD = DC
Доказательство:
Дополнительное построение, BH BD и CK AD.
Рассмотрим прямоугольные Δ BHD и ΔСKD.
В них:
НBD = DCK как накрест лежащие при BH CD (BH BD и CK AD) и секущей BC.
BD=DC по условию.
Треугольники равны по гипотенузе и острому углу.
Следовательно, BH = CK.
SABG = ½ AG * BH
SACG = ½ AG * CK
SABG = SACG
Теорема доказана.
SABG = SACG
Точка G внутри Δ АВС принадлежит медиане AD, тогда и только тогда, когда SABG=SACG

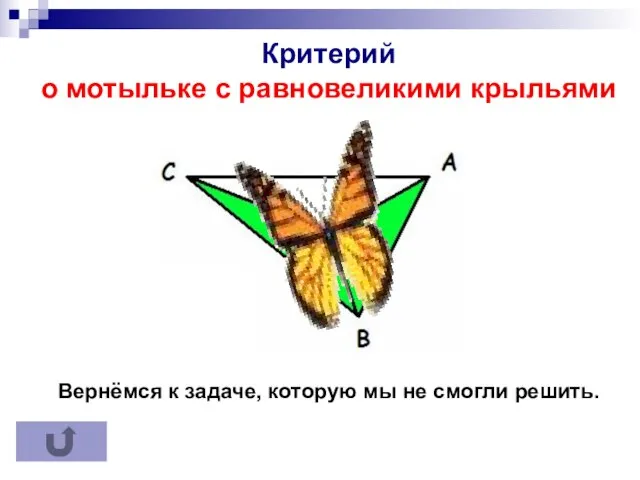
Критерий точки медианы
Критерий точки медианы
Критерий
о мотыльке с равновеликими крыльями
Вернёмся к задаче, которую мы не смогли решить.

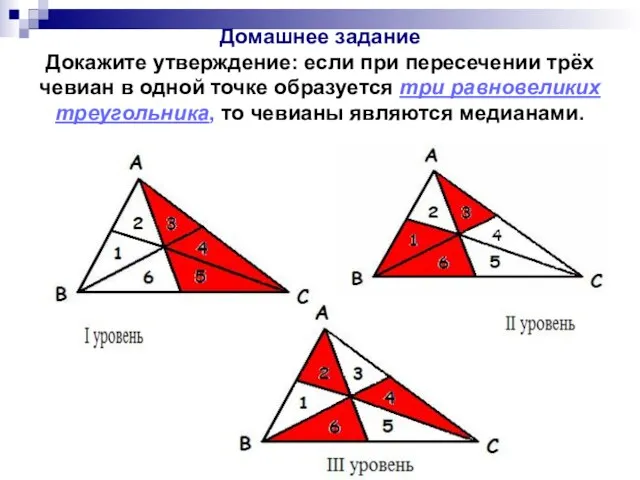
Домашнее задание
Докажите утверждение: если при пересечении трёх чевиан в одной точке образуется три равновеликих треугольника, то чевианы являются медианами.

Критерий точки медианы
Что можно утверждать, если все три треугольника
равновеликие?
Точка G является точкой пересечения медиан тогда и только тогда, когда SABG=SCBG=SAGC
Докажите это.
Критерий точки медианы
Критерий
точки пересечения медиан