Динамические модели управления запасамиЗадача управления запасами возникает, когда необходимо создать запасматериальных ресу

Перед началом решения задачи динамического управления запасами необходимо сформировать данные по этапам: просчитать затраты по каждому этапу, определить сроки возобновления заказа, режимы работы предприятия (нормальный, сверхурочный, аккордный и т.д.) Задача при отсутствии затрат на оформление заказа
Основные предпосылки модели:
1. k=0
2. Отсутствие дефицита. Спрос на продукцию не может быть удовлетворен за счет его производства в последующие периоды. Это означает, что суммарное предложение за предыдущие периоды не меньше спроса на данный момент.
3. Стоимость производства единицы продукции может изменяться в зависимости от интенсивности работы.
Модель может быть решена как транспортная задача с k*n пунктами производства и n пунктами потребления, где n – количество этапов; k – возможное число режимов работы; С
D

Алгоритм решения:
1. Построение первого опорного решения даёт оптимальное решение. Рассмотрим пример:
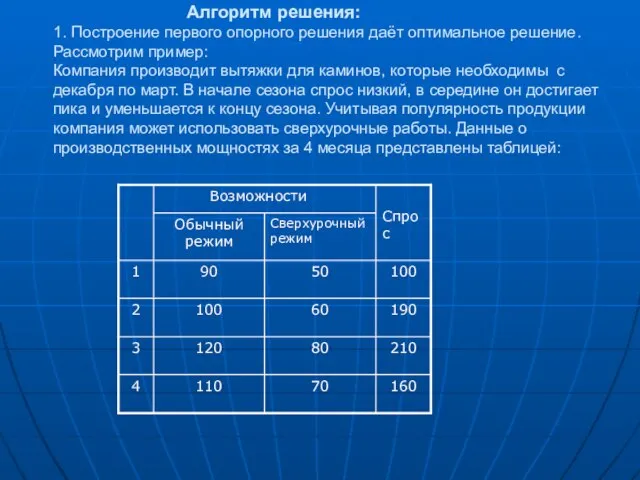
Компания производит вытяжки для каминов, которые необходимы с декабря по март. В начале сезона спрос низкий, в середине он достигает пика и уменьшается к концу сезона. Учитывая популярность продукции компания может использовать сверхурочные работы. Данные о производственных мощностях за 4 месяца представлены таблицей:

Стоимость производства единицы продукции 6 у.е. в обычном режиме и 9 у.е при сверхурочном работах. Стоимость хранения 0,1 у.е.
Решение:
90+50>=100
90+50+100+60 >=100+190
90+50+100+60+120+80>=100+190+210
500 >=500
500+10+170 >=500+160
680 >=660
Условие отсутствия дефицита выполняется.
Модель с затратами на оформление заказа.
z1 z2
x1 x2
D1 D2

zi – количество заказной продукции, i – 1, 2, … , n
Di – потребность в продукции, спрос
xi – объём запаса на начале i – го этапа
Сi = C1i + C2i, где C1i – затраты связанные с производством;
C2i – затраты связанные с хранением; 0, zi = 0
C1i = ki + Ci*zi
xi+1 = xi + zi – Di *
C2i = ( xi+zi Di)* hi – стоимость хранения единицы продукции
Т.к. в модели предполагается отсутствие дефицита, количество продукции на i-ом этапе может быть не меньше суммарной продукции реализованной на оставшихся этапах 0 < = xi+1 <= Di+1 + Di+2 + … + Di+n
Реккурентные соотношения для функции затрат fi * ( xi+1 ) минимизирующие суммарные расходы на этапах i = 1, 2, … , n будут иметь вид:
f1(x2) = min
0<= z1<= D1 + x2
k1 + C1 * z1 + h1*x2
fi(xi+1) = min
0<= zi <= Di+xi+1
ki +Ci *zi + hi*xi+1+fi-1* (xi+1 + Di – zi)
Пример:
Найти оптимальную стратегию в 3-ех этапной системе уравнения запасами , начальный запас x1= 1 ,затраты на приобретение : 10 у.е. для первых 3-ех единиц

И 20 у.е. за каждые дополнительные
x1 = 1
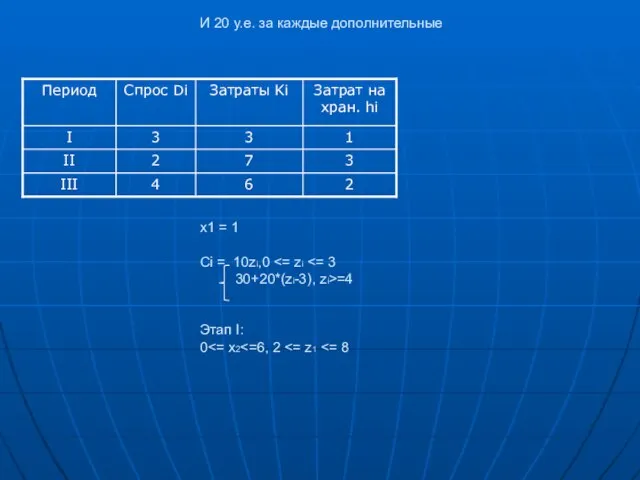
Ci = 10zi,0 <= zi <= 3
30+20*(zi-3), zi>=4
Этап I:
0<= x2<=6, 2 <= z1 <= 8

Этап III : x4 = 0 ; 0<=z3<=4
Ответ: f3(x4)min=99 y.e., z3опт=3, z2опт = 3, z1 опт = 2

Для большинства реальных ситуаций существует (положительный) срок выполнения заказа (временное запаздывание) L от момента размещения заказа до его действительной поставки. Стратегия размещения заказов в приведенной модели должна определять точку возобновления заказа.
Следующий рисунок показывает случай, когда точка возобновления заказа должна опережать на L единиц времени ожидаемую поставку. В практических целях эту информацию можно просто преобразовать, определив точку возобновления заказа через уровень запаса, соответствующий моменту возобновлению.
На практике это реализуется путем непрерывного контроля уровня запаса до момента достижения очередной точки возобновления заказа. По этой причине эту модель еще называют моделью непрерывного контроля состояния заказа. Следует заметить, что срок выполнения заказа L можно всегда принять меньше продолжительности цикла t0*.
Пример. Ежедневный спрос на некоторый товар (b ) составляет 100ед. Затраты на размещение каждого запаса (К) постоянны и равны 100долл. Ежедневные затраты на хранение единицы запаса (h) составляют 0,02долл. Определить экономичный размер партии и точку заказа при сроке выполнения заказа, равном 12 дням.
Оптимальная продолжительность цикла составляет:
t0*=у*/b = 1000/100 = 10 дней.
Т.к. срок выполнения заказа равен 12 дням и продолжительность цикла составляет 10 дней, возобновление заказа происходит, когда уровень запаса достаточен для удовлетворения спроса на 12-10=2 дня. Таким образом, заказ размером у*=1000 размещается, когда уровень запаса достигает 2*100=200ед.
Можно считать, что эффективный срок выполнения заказа равен
L- t0* при L > t0*, при этом величина (L- t0* ) меньше t0*
и равен L в противном,
здесь L - заданный срок выполнения заказа.