ДИНАМИКА ТОЧКИ

1. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
Пусть материальная точка движется вдоль оси x. Тогда во время движения y=z=0.
необходимые условия движения по прямой
Эти условия не достаточны! (см. пример)
Для того, чтобы материальная точка двигалась по прямой необходимо и достаточно, чтобы действующая на нее сила была все время параллельна начальной скорости движения точки.
Д-во достаточности: Ось x направим по начальной скорости, а начало координат совместим с начальным положением точки.

2. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ: РЕШЕНИЯ В КВАДРАТУРАХ
В силу нелинейности дифференциального уравнения, определение его решения в общем случае возможно только численно (приближенно).
Однако существуют частные случаи, в которых нахождение решения уравнения при выполнении начальных условий сводится к квадратурам – взятию интегралов.
Выделим три таких случая:

3. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ F(t)

4. ПРИМЕР: ГАРМОНИЧЕСКИ ИЗМЕНЯЮЩАЯСЯ СИЛА

5. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ F(x)

6. ПРИМЕР : ПАДЕНИЕ ЗЕМЛИ НА СОЛНЦЕ

7. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ F(dx/dt)
СПОСОБ 1
СПОСОБ 2

8. ПРИМЕР: ПАДЕНИЕ ТЕЛА С КВАДРАТИЧНЫМ СОПРОТИВЛЕНИЕМ
Приближенное решение

9. БЕЗРАЗМЕРНЫЕ ПЕРЕМЕННЫЕ
Исходная задача
Единицы измерения
Исходная задача

10. ПРЕИМУЩЕСТВА БЕЗРАЗМЕРНЫХ ПЕРЕМЕННЫХ
Проще решать. Не нужно таскать константы, труднее ошибиться
Задачу нужно решить лишь один раз, а не для каждого набора параметров. Все остальное делается простым растяжением координат x и t
Свойства изучаемого процесса проще анализировать если решение есть функция одной переменной
лучше чем

11. ПРИМЕР: ПАДЕНИЕ ТЕЛА С ЛИНЕЙНЫМ СОПРОТИВЛЕНИЕМ
Можно было бы решать как и предыдущую. Но рассматриваемое уравнение имеет огромное достоинство: оно принадлежит классу линейных диф. уравнений с постоянными коэффициентами. Метод их решения чрезвычайно прост и общ.
Рассмотрим вначале однородное диф. уравнение второго порядка с постоянными к-ми
Для построения его общего решения достаточно найти два частных решения.
Если и -такие решения, то в силу линейности -общее решение.
Частные решения легко предъявляются.
-корни квадратного ур-ния
Общее решение однородного уравнения
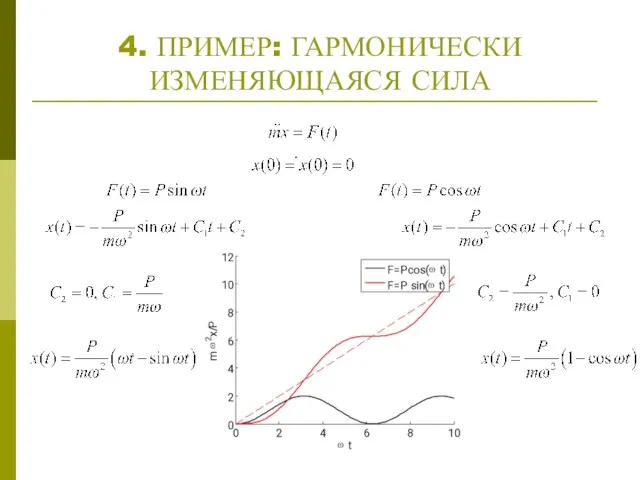
Для построения общего решения неоднородного уравнения
достаточно найти какое либо его частное решение . В силу линейности общим решением будет . Общий алгоритм построения
будет дан в курсе ДУ. Но во многих случаях просто угадывается