Содержание
- 2. О нашем курсе Курс включает Основы линейной алгебры Основы теории графов Математическую индукцию Комбинаторику Оценка 40%
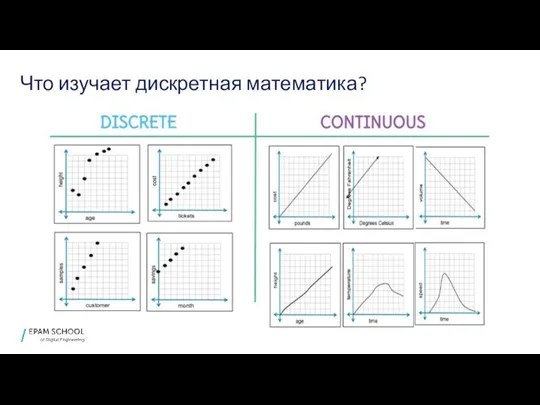
- 3. Что изучает дискретная математика?
- 4. Непрерывность – это иллюзия? Апории/трудности/парадоксы Зенона (Zeno's paradoxes) Ахиллес и черепаха Стрела Дихотомия
- 5. Линейная алгебра: что это и зачем Алгебра – это восполнение/обобщение арифметики Алгебра изучает операции над элементами
- 6. Линейная алгебра: рекомендуемые книги Письменный Д. Т. Конспект лекций по высшей математике Полный курс или Часть
- 7. Основные объекты линейной алгебры Векторы и матрицы позволяют работать с [многомерными] массивами как с числами
- 8. Обозначения и размерность матриц Матрица Размерность 2 × 3 3 × 1 1 × 3 ?
- 9. Квадратная матрица
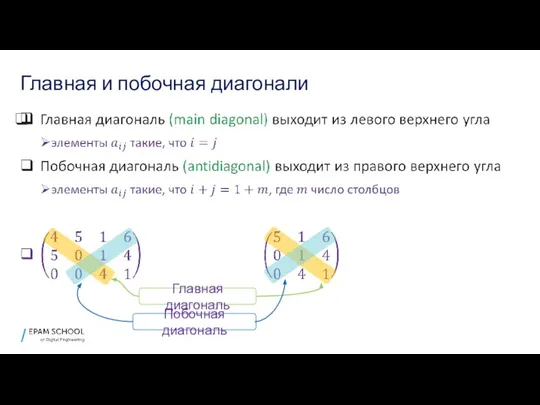
- 10. Главная и побочная диагонали
- 11. 1 и 0 в матрицах
- 12. Диагональная матрица
- 13. Транспонирование матриц ? ?
- 14. Сложение (вычитание) матриц ? ?
- 15. Умножение матрицы на скаляр (число) ? ? 1 2
- 16. Умножение матрицы на матрицу
- 17. Умножение матриц 1 0 3 -2 2 8 4 3 7 -1 0 2 5 1
- 18. Умножение матриц 1 0 3 -2 2 8 4 3 7 -1 0 2 5 1
- 19. Умножение матриц 1 0 3 -2 2 8 4 3 7 -1 0 2 5 1
- 20. Умножение матриц 1 0 3 -2 2 8 4 3 7 -1 0 2 5 1
- 21. Умножение матриц 1 0 3 -2 2 8 4 3 7 -1 0 2 5 1
- 22. Умножение матриц 1 0 3 -2 2 8 4 3 7 -1 0 2 5 1
- 23. Решим задачки ? ? ? a b c ☠ ☠ ☠ ? ? ?
- 24. Единичная матрица при умножении ? ?
- 25. Почему матричное умножение такое [сложное]? Поскольку матрица – это линейное преобразование / линейный оператор
- 26. Почему матричное умножение такое [сложное]? Поскольку таким образом легко записывать системы линейных уравнений
- 28. Скачать презентацию



![Основные объекты линейной алгебры Векторы и матрицы позволяют работать с [многомерными] массивами как с числами](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1184847/slide-6.jpg)
















![Почему матричное умножение такое [сложное]? Поскольку матрица – это линейное преобразование / линейный оператор](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1184847/slide-24.jpg)
![Почему матричное умножение такое [сложное]? Поскольку таким образом легко записывать системы линейных уравнений](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1184847/slide-25.jpg)
 Формирование познавательных универсальных учебных действийметодист Терещенко Т.И.
Формирование познавательных универсальных учебных действийметодист Терещенко Т.И. Осадчая Галина Ивановна Проректор РГСУ Руководитель научно- исследовательского комплекса доктор социологических наук, профессор
Осадчая Галина Ивановна Проректор РГСУ Руководитель научно- исследовательского комплекса доктор социологических наук, профессор 2 года
2 года Маркетинг
Маркетинг Правописание окончаний имён прилагательных мужского и среднего рода
Правописание окончаний имён прилагательных мужского и среднего рода Ученые, открывшие основные законы электротехники
Ученые, открывшие основные законы электротехники Существует такое шуточное правило: если в названии месяца есть буква р (например, январь), то в этом месяце нельзя сидеть на голой зе
Существует такое шуточное правило: если в названии месяца есть буква р (например, январь), то в этом месяце нельзя сидеть на голой зе ПРИНЦИП ПАКЕТИРОВАНИЯ
ПРИНЦИП ПАКЕТИРОВАНИЯ Стратегический план развития виртуальной компании
Стратегический план развития виртуальной компании Презентация на тему Гоголь Ревизор
Презентация на тему Гоголь Ревизор  Australian financial services consulting company (fintech)
Australian financial services consulting company (fintech)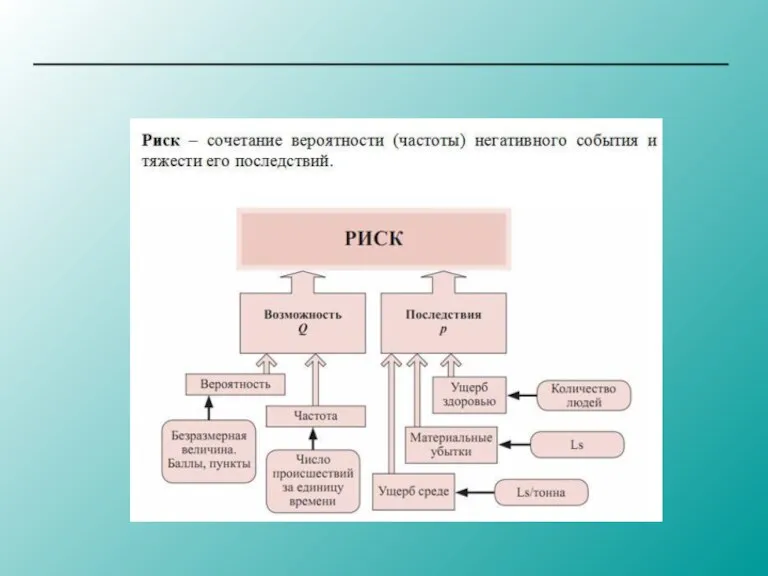 Оценка рисков
Оценка рисков Общие положения о договоре купли-продажи
Общие положения о договоре купли-продажи Художники-анималисты
Художники-анималисты Праздник цветов в Ижевске
Праздник цветов в Ижевске Родина моя – Россия
Родина моя – Россия Психологические типы личности
Психологические типы личности Новый год. Помоги бычку узнать кинозвезду!
Новый год. Помоги бычку узнать кинозвезду! Формирование системы мониторинга качества услуг учреждений культуры
Формирование системы мониторинга качества услуг учреждений культуры Сжатое изложение
Сжатое изложение печка теплица объезд штопка
печка теплица объезд штопка Основные требования к оформлению проекта
Основные требования к оформлению проекта Animals of North America
Animals of North America Координатный луч
Координатный луч Язык SQL
Язык SQL Интернет технологии в образовании
Интернет технологии в образовании Обзор
Обзор Информация в биологии
Информация в биологии