Содержание
- 2. План Звуковые сигналы и их восприятие Цифровые и аналоговые сигналы. Дискретизация. Теорема Котельникова. Алиасинг. Фильтрация звука.
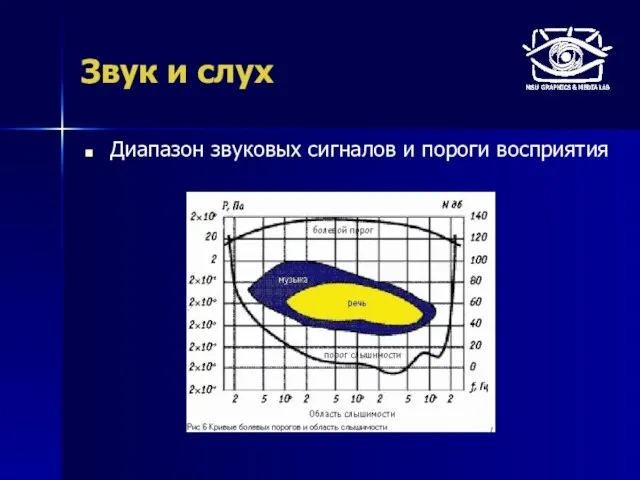
- 3. Звук и слух Диапазон звуковых сигналов и пороги восприятия
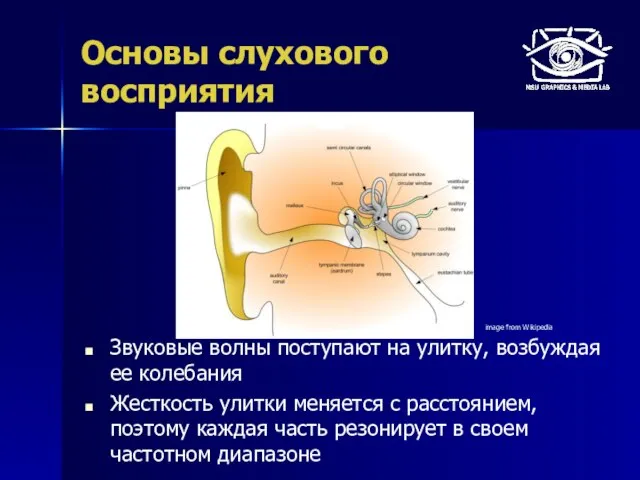
- 4. Основы слухового восприятия Звуковые волны поступают на улитку, возбуждая ее колебания Жесткость улитки меняется с расстоянием,
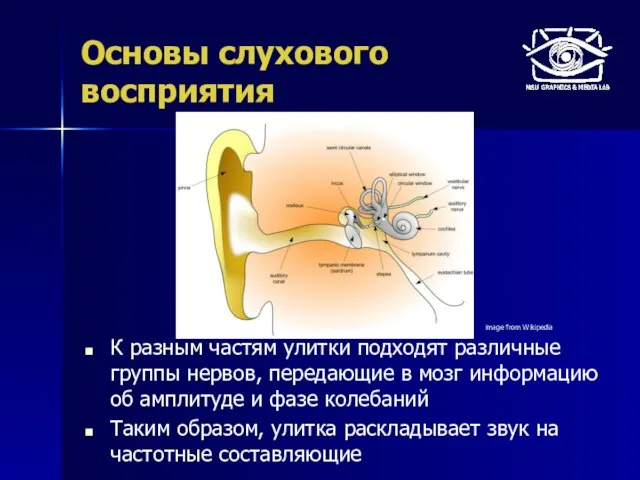
- 5. Основы слухового восприятия К разным частям улитки подходят различные группы нервов, передающие в мозг информацию об
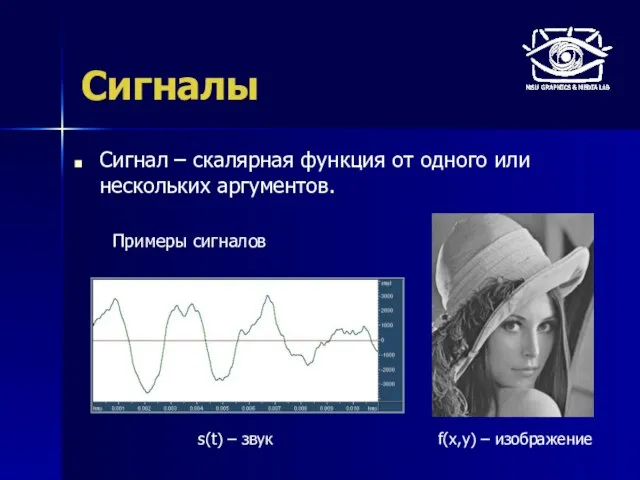
- 6. Сигналы Сигнал – скалярная функция от одного или нескольких аргументов. s(t) – звук Примеры сигналов f(x,y)
- 7. Сигналы Аналоговые (непрерывные) Примеры: звук в воздухе или в проводе, идущем от микрофона изображение (до ввода
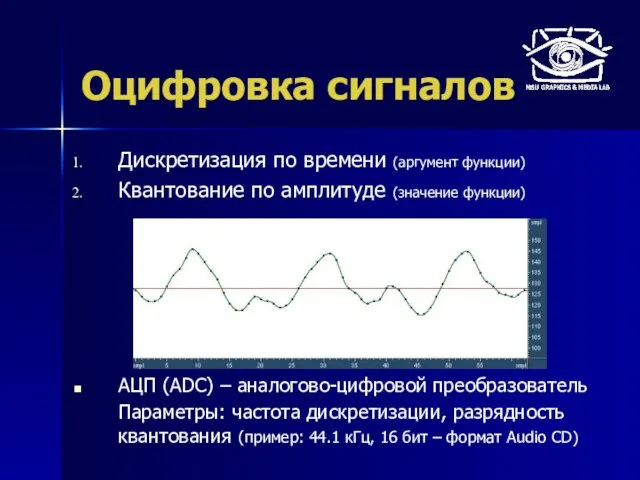
- 8. Оцифровка сигналов Дискретизация по времени (аргумент функции) Квантование по амплитуде (значение функции) АЦП (ADC) – аналогово-цифровой
- 9. Оцифровка сигналов При каких условиях по цифровому сигналу можно точно восстановить исходный аналоговый? Предположим, что значения
- 10. Теорема Котельникова Пусть спектр сигнала x(t) не содержит частот выше F, т.е. X(ν)=0 за пределами отрезка
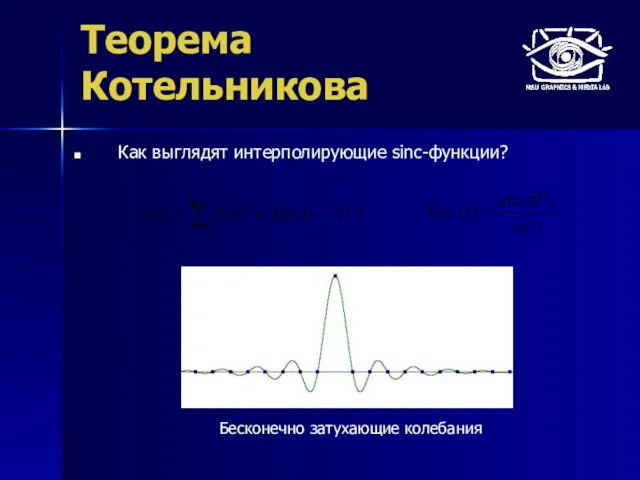
- 11. Теорема Котельникова Как выглядят интерполирующие sinc-функции? Бесконечно затухающие колебания
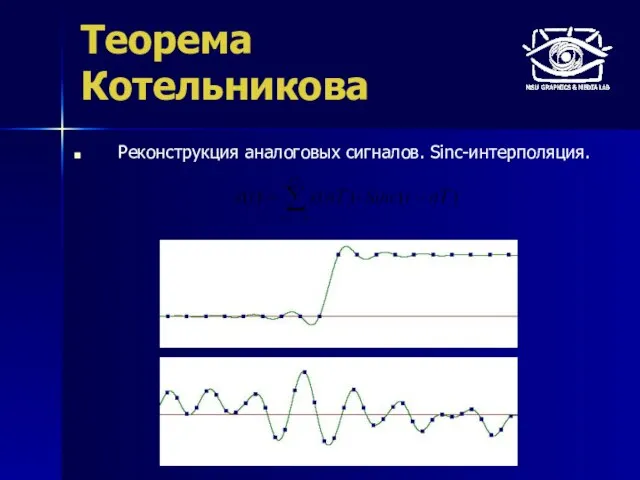
- 12. Теорема Котельникова Реконструкция аналоговых сигналов. Sinc-интерполяция.
- 13. Эффект Гиббса Применимость sinc-интерполяции для изображений Эффект Гиббса Цифровые отсчеты sinc-интерполяция другая интерполяция
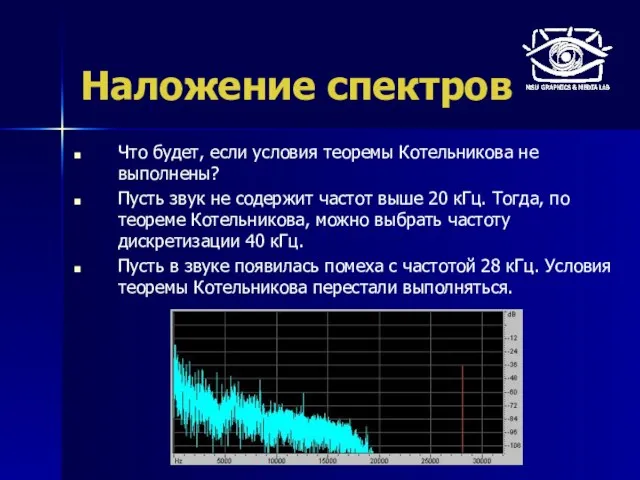
- 14. Наложение спектров Что будет, если условия теоремы Котельникова не выполнены? Пусть звук не содержит частот выше
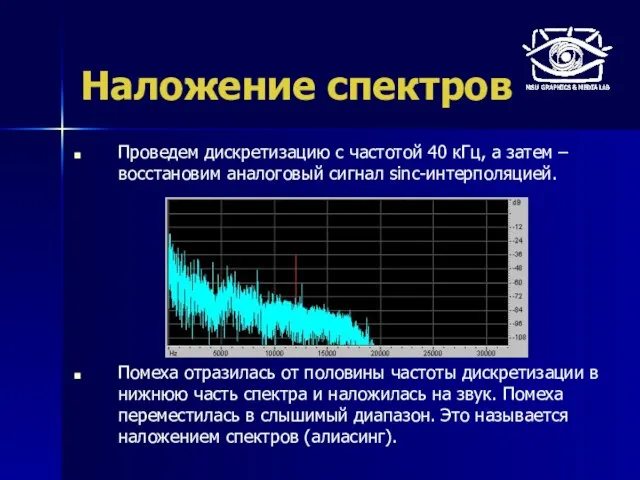
- 15. Наложение спектров Проведем дискретизацию с частотой 40 кГц, а затем – восстановим аналоговый сигнал sinc-интерполяцией. Помеха
- 16. Наложение спектров Как избежать наложения спектров? Применить перед оцифровкой анти-алиасинговый фильтр Он подавит все помехи выше
- 17. Линейные системы Система – преобразователь сигнала. Линейность: Инвариантность к сдвигу: H x(t) y(t)
- 18. Импульсная характеристика Единичный импульс δ[n] Разложение произвольного сигнала на взвешенную сумму единичных импульсов
- 19. Импульсная характеристика Отклик системы на единичный импульс h[n] – импульсная характеристика системы (импульсный отклик системы)
- 20. Импульсная характеристика Вычисление отклика линейной системы на произвольный входной сигнал Свертка h[n] – ядро свертки
- 21. Линейные системы Итак, любая линейная инвариантная к сдвигу система производит операцию свертки входного сигнала со своей
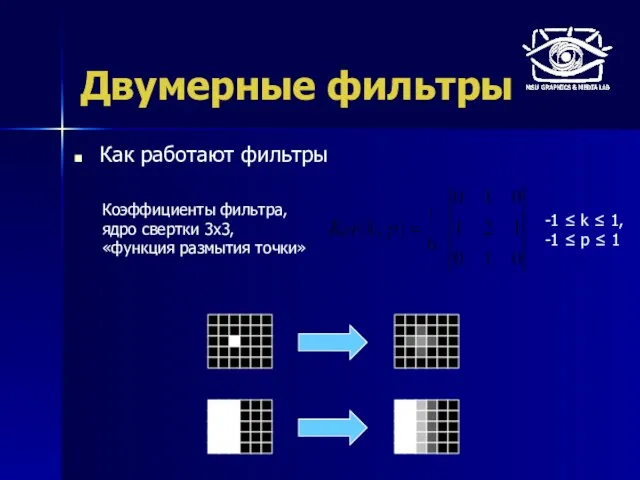
- 22. Двумерные фильтры Как работают фильтры Коэффициенты фильтра, ядро свертки 3x3, «функция размытия точки» -1 ≤ k
- 23. Двумерные фильтры Свертка // Обнулить изображение Dest[i][j] ... // Выполнить свертку for (i=0; i for (j=0;
- 24. Двумерные фильтры Свойства фильтров Результат фильтрации однотонного (константного) изображения – константное изображение. Его цвет равен Следствие:
- 25. Примеры фильтров Размытие (blur)
- 26. Примеры фильтров Повышение четкости (sharpen)
- 27. Примеры фильтров Нахождение границ (edges)
- 28. Примеры фильтров Тиснение (embossing)
- 29. Примеры фильтров Простейшее размытие Константное размытие “box-фильтр” (любой размер фильтра) Гауссово размытие (любой размер фильтра)
- 30. Примеры фильтров Повышение резкости Нахождение границ Тиснение + модуль, нормировка, применение порога… + сдвиг яркости, нормировка…
- 31. Двумерные фильтры Свойства двумерной свертки (повторение) Линейность Инвариантность к сдвигу Пусть X и Y – изображения,
- 32. Двумерные фильтры Сепарабельные (разделимые) фильтры Гауссиан – сепарабельный фильтр, т.к. Если фильтр сепарабельный, то фильтрацию можно
- 33. Двумерные фильтры Unsharp Mask Параметры: радиус, сила эффекта, порог срабатывания Идея: вычесть из изображения его размытую
- 34. Двумерные фильтры Медианный фильтр Каждый пиксель принимает значение, являющееся медианой значений пикселей в окрестности Медиана –
- 35. Двумерные фильтры Медианный фильтр 5x5
- 36. Двумерные фильтры Понятие о частотах в изображении и звуке Частоты и гармонические колебания (звук) Частоты и
- 37. Преобразование Фурье Зачем раскладывать сигналы на синусоиды? Анализ линейных систем Слух и синусоиды Хорошо разработана теория
- 38. Преобразование Фурье Базисные функции дискретного преобразования Фурье для сигнала длины N = 8. Имеем N/2 +
- 39. Преобразование Фурье Базисные функции образуют N-мерный ортогональный базис в пространстве N-мерных векторов исходных сигналов. Следовательно, разложение
- 40. Преобразование Фурье Прямое преобразование Фурье – вычисление скалярных произведений сигнала на базисные функции: Для вычисления всех
- 41. Преобразование Фурье Быстрое преобразование Фурье (БПФ, FFT) – ускоренный алгоритм вычисления ДПФ Основан на периодичности базисных
- 42. Преобразование Фурье Входные данные FFT N = 2m, размер FFT Входной вектор длины N, иногда в
- 43. Преобразование Фурье Двумерное ДПФ Базисные функции имеют вид двумерных синусоид с разными углами наклона и фазами
- 44. Преобразование Фурье Быстрое вычисление двумерного ДПФ Вычислить одномерные комплексные ДПФ от каждой строки изображения. Результаты записать
- 45. Спектральный анализ Как вычислить и отобразить спектр сигнала? Взять нужный отрезок сигнала длины 2m; если нужный
- 46. Спектральный анализ Отображение спектров изображений Спектр – это картинка, показывающая зависимость амплитуды от частоты и от
- 47. Спектральный анализ Примеры изображений и их спектров Видно, что спектр одной синусоиды – это точка (не
- 48. Спектральный анализ Примеры изображений и их спектров По спектру прослеживаются преобладающие направления в исходной картинке Много
- 49. Спектральный анализ Отображение спектра звука: спектр Спектр – график зависимости амплитуды от частоты Низкие частоты –
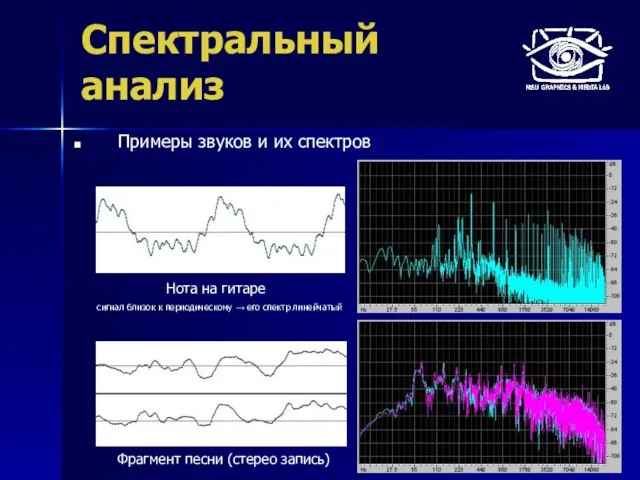
- 50. Спектральный анализ Примеры звуков и их спектров Фрагмент песни (стерео запись) Нота на гитаре сигнал близок
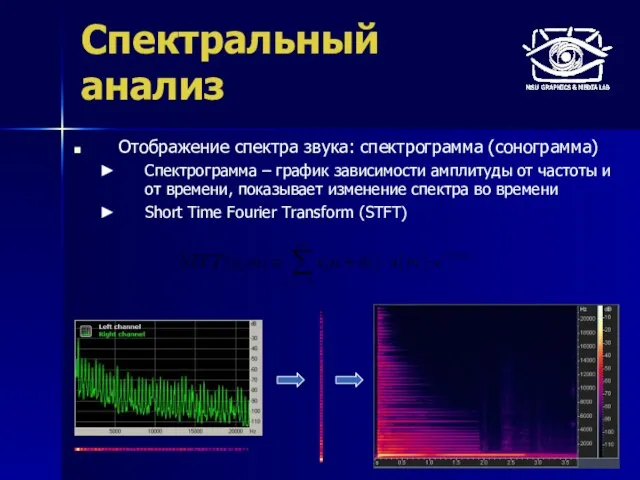
- 51. Спектральный анализ Отображение спектра звука: спектрограмма (сонограмма) Спектрограмма – график зависимости амплитуды от частоты и от
- 52. Спектральный анализ Отображение спектра звука: спектрограмма (сонограмма) Спектрограмма – график зависимости амплитуды от частоты и от
- 54. Скачать презентацию







![Импульсная характеристика Единичный импульс δ[n] Разложение произвольного сигнала на взвешенную сумму единичных импульсов](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/395367/slide-17.jpg)
![Импульсная характеристика Отклик системы на единичный импульс h[n] – импульсная характеристика системы (импульсный отклик системы)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/395367/slide-18.jpg)
![Импульсная характеристика Вычисление отклика линейной системы на произвольный входной сигнал Свертка h[n] – ядро свертки](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/395367/slide-19.jpg)

![Двумерные фильтры Свертка // Обнулить изображение Dest[i][j] ... // Выполнить свертку for](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/395367/slide-22.jpg)



























 Ислам. Тест
Ислам. Тест Концепция структурных преобразований радиоэлектронной промышленности оборонно-промышленного комплекса
Концепция структурных преобразований радиоэлектронной промышленности оборонно-промышленного комплекса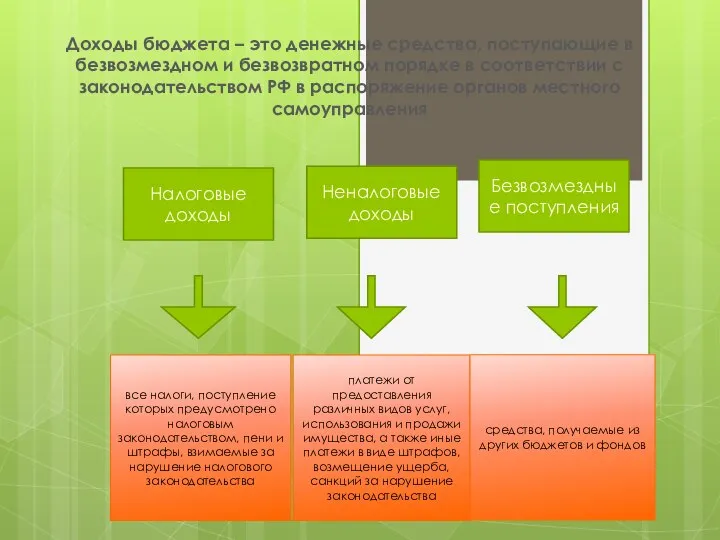 Доходы бюджета Чугунаевского сельского поселения
Доходы бюджета Чугунаевского сельского поселения Деды Морозы в разных странах
Деды Морозы в разных странах Презентация на тему Дорожное движение, безопасность участников дорожного движения (5 класс)
Презентация на тему Дорожное движение, безопасность участников дорожного движения (5 класс) Конкурсная программа «Мы должны быть бережливыми!»
Конкурсная программа «Мы должны быть бережливыми!» Галерея помещиков Мёртвые души
Галерея помещиков Мёртвые души Искусство второй половины XX века.Ташизм, абстрактный экспрессионизм
Искусство второй половины XX века.Ташизм, абстрактный экспрессионизм Производство ферментных препаратов
Производство ферментных препаратов  Общая физическая подготовка
Общая физическая подготовка Придаточные предложения места
Придаточные предложения места Main changes Tudors
Main changes Tudors Сертификация (ап)
Сертификация (ап) Презентация к уроку русского языка в 6 классе по теме Прилагательное как часть речи Составитель: Падалко Татьяна Викторовна
Презентация к уроку русского языка в 6 классе по теме Прилагательное как часть речи Составитель: Падалко Татьяна Викторовна  Презентация на тему Характер
Презентация на тему Характер Организация и нормативно-правовое обеспечение государственной (итоговой) аттестации выпускников 9-х классов в 2009-2010 учебном
Организация и нормативно-правовое обеспечение государственной (итоговой) аттестации выпускников 9-х классов в 2009-2010 учебном  Александр Сергеевич Пушкин
Александр Сергеевич Пушкин Ответственность директоров и контролирующего лица
Ответственность директоров и контролирующего лица Организация внеурочной деятельности при реализации федерального государственного образовательного стандарта начального общего
Организация внеурочной деятельности при реализации федерального государственного образовательного стандарта начального общего Презентация на тему Загадки с подвохом
Презентация на тему Загадки с подвохом Век XVIII в истории России
Век XVIII в истории России Законы и нормативно-правовые акты по организации безопасности по условиям РСЧС
Законы и нормативно-правовые акты по организации безопасности по условиям РСЧС БОРТОВАЯ АНАЛИТИЧЕСКАЯ СИСТЕМА УПРАВЛЕНИЯ РИСКАМИ ПОЛЕТА САМОЛЕТА
БОРТОВАЯ АНАЛИТИЧЕСКАЯ СИСТЕМА УПРАВЛЕНИЯ РИСКАМИ ПОЛЕТА САМОЛЕТА ИМИДЖ КАК ФАКТОР КОНКУРЕНТОСПОСОБНОСТИ ВЫСШЕГО УЧЕБНОГО ЗАВЕДЕНИЯ
ИМИДЖ КАК ФАКТОР КОНКУРЕНТОСПОСОБНОСТИ ВЫСШЕГО УЧЕБНОГО ЗАВЕДЕНИЯ Формы ДНК
Формы ДНК Инфекционный перитонит кошек
Инфекционный перитонит кошек Правила выплат нуждающимся в поддержке семьям на детей от 3 до 7 лет
Правила выплат нуждающимся в поддержке семьям на детей от 3 до 7 лет S-Иерархия и атрибуты маршрутов
S-Иерархия и атрибуты маршрутов