ДОКЛАД УЧИТЕЛЯ МАТЕМАТИКИ Копыловой Т. Ю. ДАЛЬТОН-дом

ОСНОВНАЯ ИДЕЯ ДАЛЬТОН-ТЕХНОЛОГИИ:
работай с кем хочешь;
спрашивай кого хочешь;
но отвечать за выполнение задания будешь сам.

Все эти исходные позиции философии рассматриваемой технологии реализуются через ДАЛЬТОН-ПЛАН, включающий в себя задания, лабораторию и «дом».

ДАЛЬТОН-ПЛАН –
это сочетание кабинетного обучения с образовательным процессом, основанном на трёх принципах:
свобода,
самостоятельность,
сотрудничество.

«Дом» – это условия, приближенные к домашней свободе: наличие места, где ученику комфортно работать; свобода выбора с кем выполнять работу; наличие группы консультантов.
Для общения детей необходимы отдельные столы, рабочие уголки. Рядом со столом учителя – стулья для учащихся, которые ждут своей очереди к учителю. Необходимо также иметь источники информации в классе или библиотеке, открытые кабинеты с наглядными пособиями;

Система действий учителя и ученика
Классное учебное занятие
Коллективный урок
Лабораторное занятие
Конференция

КОНФЕРЕНЦИЯ
Отличительная черта конференции состоит в организации обсуждения теоретического вопроса, желательно интегративного характера. Особое значение уделяется человеческим проблемам, ценностям и т.п.
Основные признаки конференции:
необходимость подготовительного этапа;
выступления в форме докладов, а не сообщений, т.е. в выступлениях важно обозначить собственную позицию.

Нахождение площади решётчатого многоугольника.

АКТУАЛЬНОСТЬ.
Среди заданий ЕГЭ по математике есть задачи на нахождение площадей фигур, в частности, площадей решетчатых многоугольников:
( задания В6 – ЕГЭ 2010,2011 годов,
В3 – ЕГЭ 2012 года)

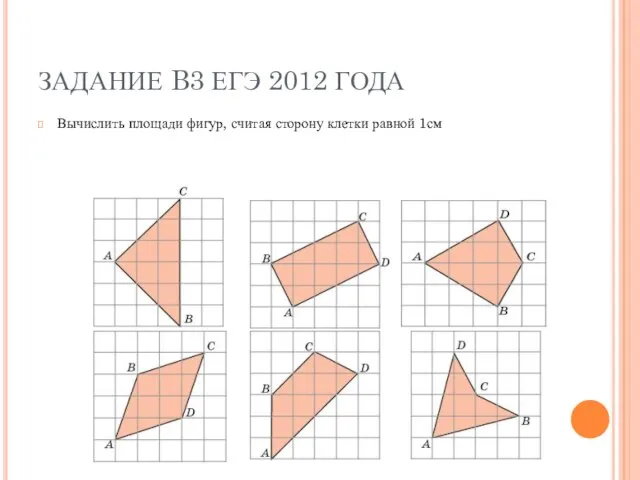
ЗАДАНИЕ B3 ЕГЭ 2012 ГОДА
Вычислить площади фигур, считая сторону клетки равной 1см

ОПРЕДЕЛЕНИЕ
Многоугольник — фигура на плоскости, ограниченная замкнутой ломаной.
Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами или на узлах решетки ( клетки)

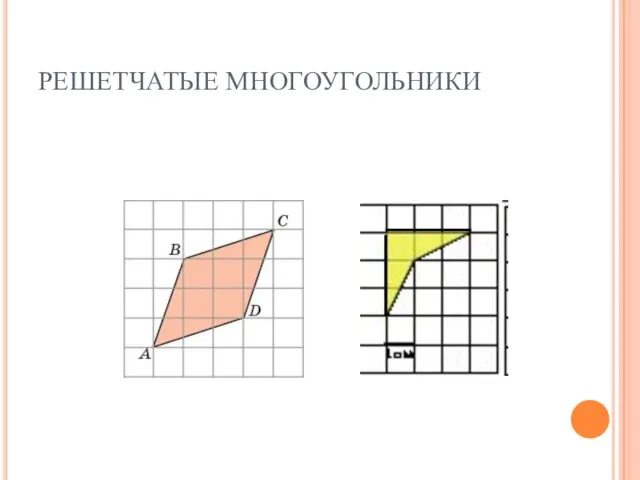
РЕШЕТЧАТЫЕ МНОГОУГОЛЬНИКИ

Способы нахождения площадей решетчатых многоугольников

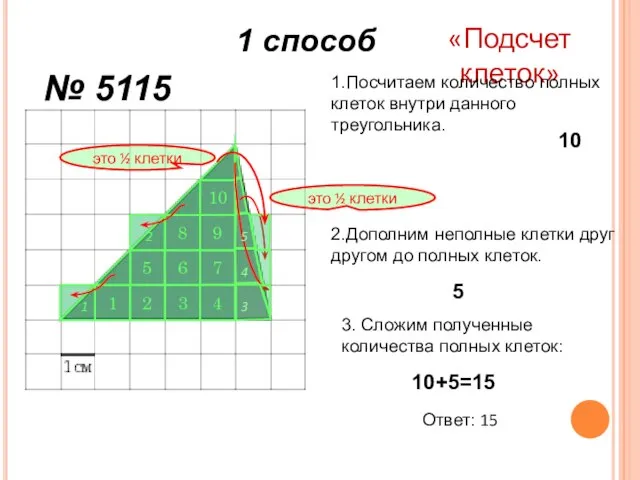
7
3
1
2
4
5
6
8
9
10
№ 5115
1 способ
«Подсчет клеток»
1.Посчитаем количество полных клеток внутри данного треугольника.
10
2.Дополним неполные клетки друг другом до полных клеток.
5
3. Сложим полученные количества полных клеток:
10+5=15
Ответ: 15
1
2
3
4
это ½ клетки
это ½ клетки
5

« ПРИМЕНЕНИЕ ФОРМУЛ ПЛОЩАДЕЙ ИЗВЕСТНЫХ ФИГУР»
2 способ

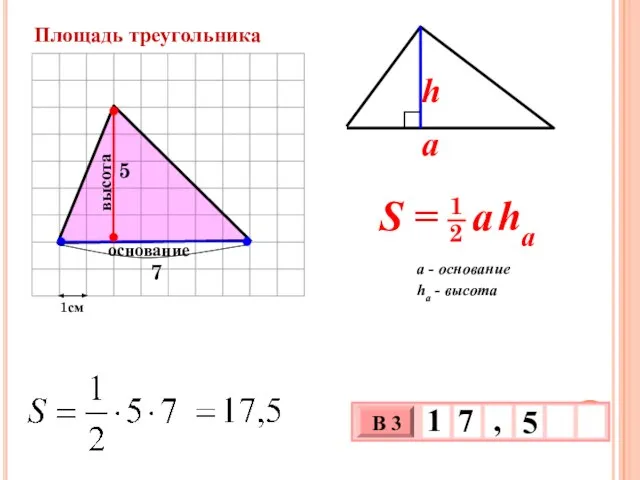
1см
5
основание
высота
Площадь треугольника

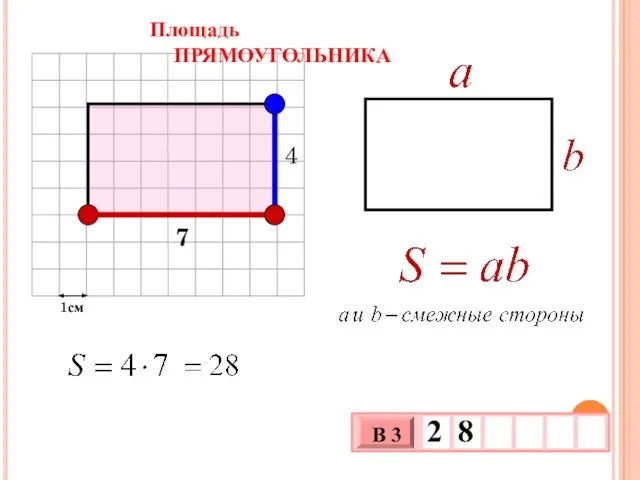
1см
Площадь ПРЯМОУГОЛЬНИКА
7
4

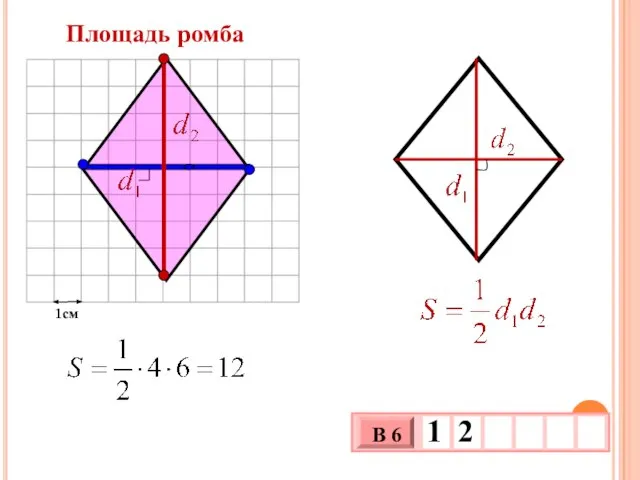
1см
Площадь ромба

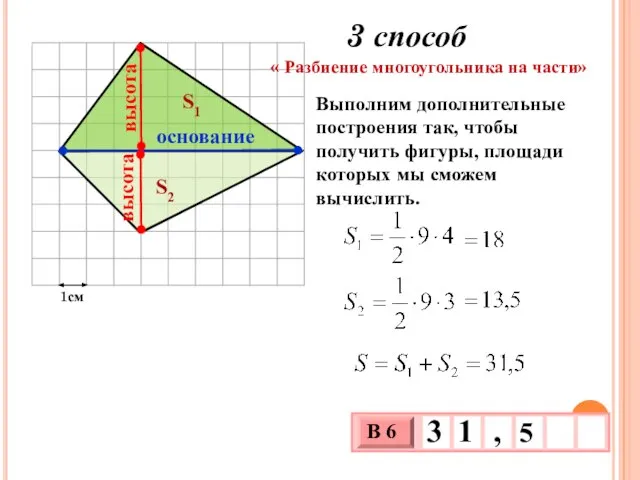
1см
S1
S2
3 способ
« Разбиение многоугольника на части»
Выполним дополнительные построения так, чтобы получить фигуры, площади которых мы сможем вычислить.

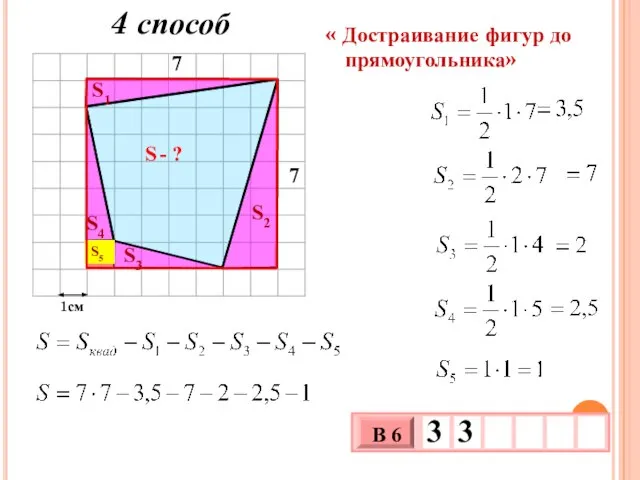
1см
S - ?
S1
S4
S2
S5
S3
« Достраивание фигур до прямоугольника»
4 способ