Содержание
- 2. «Математика и музыка требуют единого мыслительного процесса» (А. Энштейн)
- 3. . Основополагающий вопрос: Почему еще в древности утверждали, что математика и музыка - сестры? Цель исследования:
- 4. Задачи исследования: овладеть методикой и навыками ведения исследовательской работы; определить взаимосвязи между обыкновенными дробями и длительностью
- 5. Методы исследования анализ синтез сравнение обобщение
- 6. Исследования проводили группы Историки Теоретики Практики
- 7. Пифагор (ок. 570- ок. 550 гг. до н.э.) Древнегреческий философ Пифагор, один из самых первых установил
- 8. Используя особый инструмент - монохорд, Пифагор изучал интервалы, открывал математические соотношения между отдельными звуками.
- 9. «Число правит миром» Пифагорейцы верили, что в числовых закономерностях спрятана тайна мира. Пифагор открыл, что основные
- 10. Для определения музыкально – математической связи обыкновенных дробей с длительностью нот проводились следующие исследования: совпадения длительности
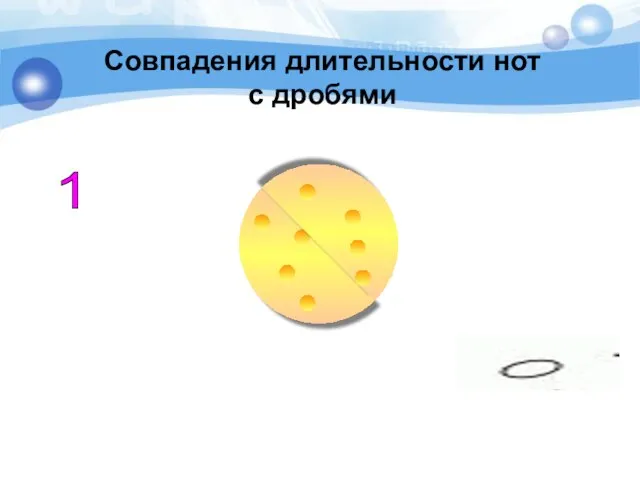
- 11. 1 Совпадения длительности нот с дробями
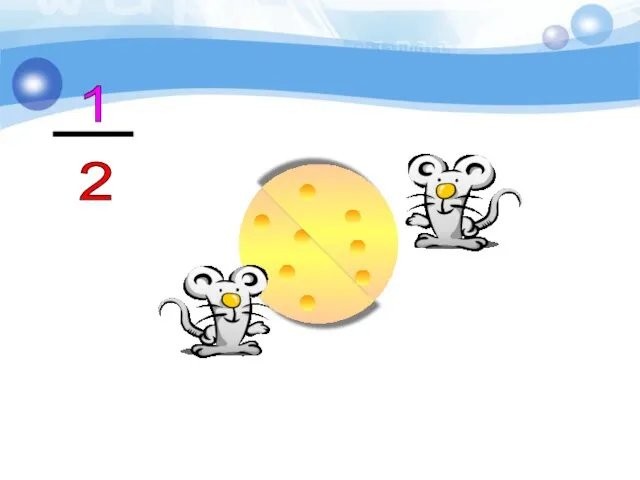
- 12. 1 2
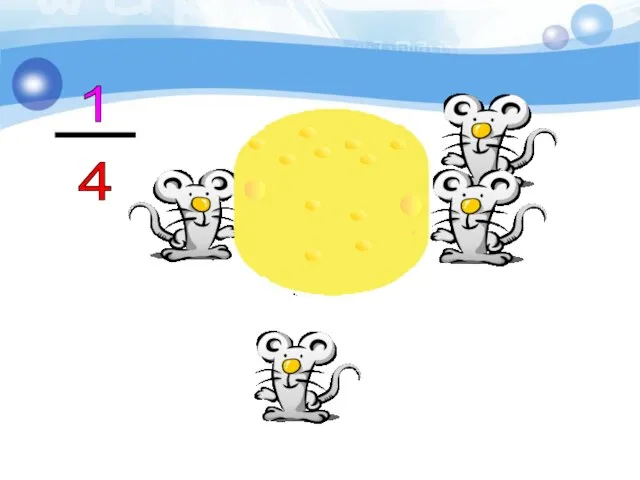
- 13. 1 4
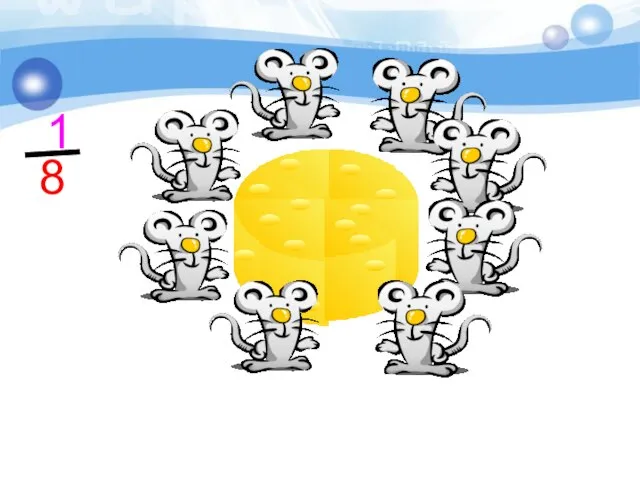
- 14. 1 8
- 15. Действия сложения и вычитания с длительностями нот 1/4 = 1/8 + 2/16 .
- 16. Нотные равенства Действия с дробями 1/8 + 1/8 = 1/4 1/4 + 1/4 = 1/2 1
- 17. Сравнения длительности нот и дробей 1 1/2 1/4 1/8 1/16
- 18. Длина такта 1/2 + 1/4 + 1/8 + 1/8 = 1
- 20. Фрагмент русской народной песни «Ах вы, сени, мои сени» Нотная грамота Запись математических вычислений
- 21. Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник,
- 22. . 3 5 4 Вывод В результате работы над проектом было доказано, что математика и музыка
- 23. С музыкою веселей Изучение дробей. А без дроби так и сяк Будет в нотах кавардак
- 25. Скачать презентацию


















 Поколение молодости REV 7-2014
Поколение молодости REV 7-2014 Взаимодействие агентов в многоагентных системах
Взаимодействие агентов в многоагентных системах ФАКТОГРАФИЧЕСКИЕ БАЗЫ ДАННЫХ НАЦИОНАЛЬНОЙ БИБЛИОТЕКИ БЕЛАРУСИ КАК ИСТОЧНИК ИНФОРМАЦИИ О НАЦИОНАЛЬНЫХ ОБЪЕКТАХ Кузьминич Т. Нац
ФАКТОГРАФИЧЕСКИЕ БАЗЫ ДАННЫХ НАЦИОНАЛЬНОЙ БИБЛИОТЕКИ БЕЛАРУСИ КАК ИСТОЧНИК ИНФОРМАЦИИ О НАЦИОНАЛЬНЫХ ОБЪЕКТАХ Кузьминич Т. Нац Филиппова Елена Константиновна – учитель Филиппова Елена Константиновна – учитель русского языка и литературы Квалификационная
Филиппова Елена Константиновна – учитель Филиппова Елена Константиновна – учитель русского языка и литературы Квалификационная Новости недели. Новосибирск
Новости недели. Новосибирск Художники Сенгилеевского района
Художники Сенгилеевского района ПрезентацияРаздел 2.2
ПрезентацияРаздел 2.2 Международные модели управления персоналом
Международные модели управления персоналом Цели внедрения системы бюджетирования
Цели внедрения системы бюджетирования Деление плоскости на четыре части, в зарисовке
Деление плоскости на четыре части, в зарисовке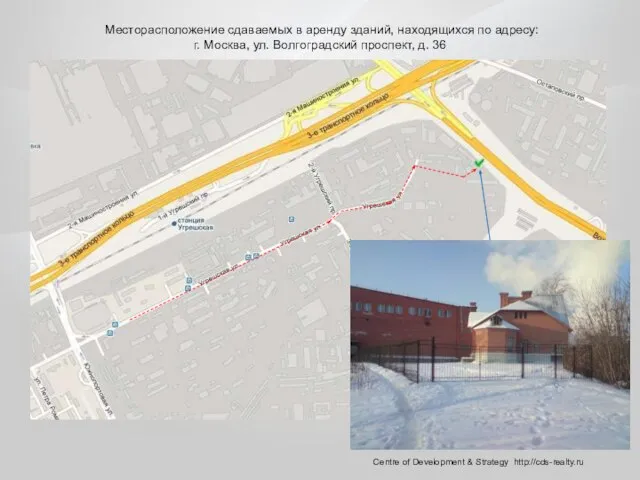 Месторасположение сдаваемых в аренду зданий, находящихся по адресу: г. Москва, ул. Волгоградский проспект, д. 36
Месторасположение сдаваемых в аренду зданий, находящихся по адресу: г. Москва, ул. Волгоградский проспект, д. 36 Филимоновская игрушка. Фотоотчет
Филимоновская игрушка. Фотоотчет Фридрих Шиллер
Фридрих Шиллер Презентация на тему Особые экономические зоны стран мира
Презентация на тему Особые экономические зоны стран мира  Фотоэлектрические модули. (Лекция 5)
Фотоэлектрические модули. (Лекция 5) The Victorian Era 1837 -1901
The Victorian Era 1837 -1901 Династический кризис 1825 г. Выступление декабристов
Династический кризис 1825 г. Выступление декабристов ВЕЛИКАЯ ОТЕЧЕСТВЕННАЯ ВОЙНА СОВЕТСКОГО СОЮЗА.
ВЕЛИКАЯ ОТЕЧЕСТВЕННАЯ ВОЙНА СОВЕТСКОГО СОЮЗА. Электронное взаимодействие между организациями ислужбой занятости населения
Электронное взаимодействие между организациями ислужбой занятости населения Порядок подачи заявления о преступлении
Порядок подачи заявления о преступлении Избушка
Избушка Сказочный мир Шарля Перро
Сказочный мир Шарля Перро ПОП-АРТ
ПОП-АРТ Осенние поделки
Осенние поделки Управление эмоциями
Управление эмоциями КОТЕЛЬНАЯ 4 Х 15 МВт
КОТЕЛЬНАЯ 4 Х 15 МВт Основные этапы разработки ООП
Основные этапы разработки ООП «Свирель серебряного века»
«Свирель серебряного века»