Содержание
- 2. Появление процн\ \ Появление про % Интересно его происхождение. Появился он в результате опечатки: наборщик переставил
- 3. Опорные сведения. *Процентом (от лат.pro cento – от сотни) от любой величины, в том числе и
- 4. Задачи на проценты Процент от данного числа. Например, 1% от зарплаты это сотая часть зарплаты; 100%
- 5. ПРИМЕРЫ 1.Подоходный налог взимается в размере 13% от суммы, превышающей минимальную заработную плату. Найти величину налога,
- 6. Сколько процентов составляет одна величина от другой 1.Какой проект более выгодный? Расход на первый 1000000 руб.
- 7. При изменении величины процент ее увеличения или уменьшения всегда устанавливается по отношению к прежнему значению этой
- 8. Количественные изменения Для того, чтобы описать количественные изменения величин, указывают, во сколько раз они увеличились или
- 9. К процентам чаще прибегают для рекламы, кратные используют дл я наглядности. Сравните фразы: «Увеличение в10раз» «Увеличение
- 10. 1.Какие из утверждений означают одно и тоже: Цена увеличилась в 2 раза; Цена увеличилась на 100%;
- 11. Употребляя слово «процент», следует точно понимать, от чего именно берется этот процент. Пример 1. Цена на
- 12. Вариант 1. Увеличение товарооборота в январе составило 15%, а в феврале 24%. На сколько увеличился товарооборот
- 13. Вариант 2. Средняя семья платит за квартиру 8 тыс. руб. в месяц. Это составляет 20% того,
- 14. Сложные проценты Формула сложных процентов a-первоначальная величина, которая через определенные промежутки увеличивается , возрастая каждый раз
- 16. Скачать презентацию













 История развития гидравлики
История развития гидравлики Теория детской игры Эльконина Даниила Борисовича
Теория детской игры Эльконина Даниила Борисовича Қисық11А
Қисық11А Электроэнергетика 10 класс
Электроэнергетика 10 класс Народные промыслы России
Народные промыслы России Климат - сервис
Климат - сервис Презентация на тему Израиль
Презентация на тему Израиль  ООО Завод Модульных Конструкций - один из крупнейших в РФ, по изготовлению Блок контейнеров
ООО Завод Модульных Конструкций - один из крупнейших в РФ, по изготовлению Блок контейнеров Гуторова Олеся Ивановна. Диплом
Гуторова Олеся Ивановна. Диплом Врожденный гипотиреоз
Врожденный гипотиреоз 08. Произведение вектора на число
08. Произведение вектора на число Презентация на тему Лекарства и их виды
Презентация на тему Лекарства и их виды  Армия Казахстана
Армия Казахстана Итоги работы отрасли и основные направления инновационного развития легкой промышленности
Итоги работы отрасли и основные направления инновационного развития легкой промышленности Лекция 4 - Вывод нелинейных УУН для сети переменного тока
Лекция 4 - Вывод нелинейных УУН для сети переменного тока БИОЛОГИЯ И ПАТОЛОГИЯ РЫБ
БИОЛОГИЯ И ПАТОЛОГИЯ РЫБ Лёгкая атлетика. Прыжки в длину
Лёгкая атлетика. Прыжки в длину Транспорт России
Транспорт России Зоологический музей имени Э.А. Эверсмана
Зоологический музей имени Э.А. Эверсмана Дело о трех картах
Дело о трех картах День европейский языков
День европейский языков Лот 13, г. Хабаровск, ул. Сысоева, 21, кв. 19
Лот 13, г. Хабаровск, ул. Сысоева, 21, кв. 19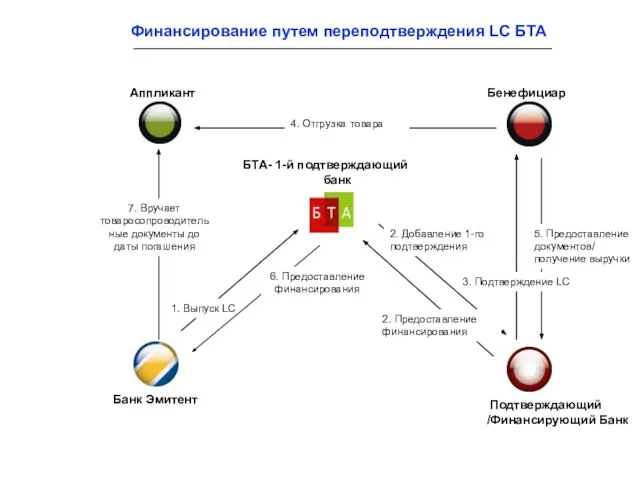 Финансирование путем переподтверждения LC БТА
Финансирование путем переподтверждения LC БТА Звіт основні орієнтири 2 клас 2013
Звіт основні орієнтири 2 клас 2013 Презентация на тему Бунге - министр финансов
Презентация на тему Бунге - министр финансов 04.07.201204.07.2012Eurasia - Institut EURASIA Institute, Berlin. - презентация
04.07.201204.07.2012Eurasia - Institut EURASIA Institute, Berlin. - презентация ХАНС ХОЛЬБЕН МЛАДШИЙ
ХАНС ХОЛЬБЕН МЛАДШИЙ Цветок
Цветок