Слайд 2Условия задачи
Тело брошено со скоростью V под углом @ к горизонту.

Определить:
Траекторию движения тела
Время полёта
Дальность полёта
Максимальную высоту подъёма H
Скорость тела на высоте hНормальное и тангенсальное ускорения в начальной точке траектории и в наивысшей точке подъёма
Радиусы кривизны в этих точках
Слайд 3Дано:
V, @
Решение:
Найти:
1)Уравнения движения
2) t
3) l
4) H max
5) V
6) a , a t
7)

R
Слайд 4y
x
g
voy
vox
@
l
S
vo
vx2
vh2
vy2
B1
B2
Движение данного тела в системе координат.
График
А
.
0
h
h
Vh1
Vy1
Vx1
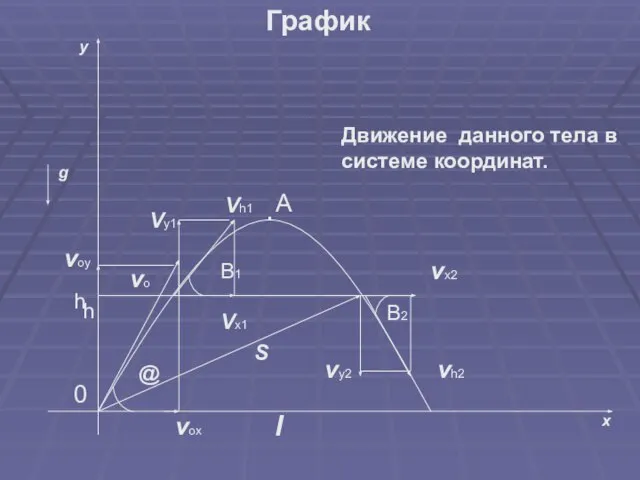
Слайд 5Решение
Движение тела вдоль оси x равномерное(ax=0);V0x = Vocos@, причем Vx=V0x=const. Уравнение

движения вдоль оси x имеет вид:
x = x0xt = v0xtcos@
Движение по оси y равнопеременное с ускорением ау = -g = const и начальной скоростью Voy = V0sin@; Vy = Voy – gt.
Уравнение движения вдоль оси у имеет вид:
y = Voyt – gt^2/2 = V0tsin@ - gt^2/2
Слайд 6
Найти траекторию движения – это значит найти аналитическое уравнение кривой, по которой

движется тело в пространстве. Т. к. t = x/V0cos@ , то
y = xtg@ - gx^2/2V0^2cos^2@ .
2. Найдём t ,приравняв y = V0tsin@ - gt^2/2 к 0:
t(V0sin@ - gt/2) = 0
t1=0 t2 = (2V0/g)sin@
Действительно, тело на земле оказывается дважды - в начале и в конце полёта.
Слайд 73) Т. к. вдоль оси x движение равномерное и известно время движения,

то
xmax = l = V0xt = (V0cos@2V0sin@)/g = =V0^2sin2@/g
4) Hmax можно найти через время подъёма tпод. Т. к. в точке Нmax Vy=0, то
0 = V0y – gtпод
tпод = (V0/g)sin@
Таким образом,
Ymax = Hmax = V0ytпод – V0yt под ^2/2 = V0y^2/2g
Hmax = (V0^2sin^2@)/2g.
Слайд 85) Для определения скорости на высоте h необходимо знать время, когда тело

находиться на этой высоте, th
Vx = V0x, Vy = V0y – gth
y = h = V0yth – gth^2/2
(th)1,2 = V0y+/- V0y^2 – 2gh
g
Скорость в первой точке при th1
Vx1 = V0cos@
Vy1 = (V0^2sin^2@ - 2gh)
Слайд 9Модуль скорости равен Vh 1 = V0^2-2gh,
тангенс угла наклона скорости к

оси х:
tgB1=Vy1/Vx1 = V0^2sin^2@ – 2gh
V0cos@
Скорость во второй точке при th2
Vx2 = V0cos@
Vy2 = - V0^2sin^2@ - 2gh
Модуль скорости равен Vh 2 = V0^2-2gh,
тангенс угла наклона скорости к оси х:
tgB1=Vy1/Vx1 = - V0^2sin^2@ – 2gh
V0cos@
Слайд 106)В точке О
a0 = -gcos@ а0t = -gsin@
В точке

А
аА = -g atA = 0
7)Нормальное ускорение определяется по формуле
а = V^2/R R = V^2/a, где R – радиус кривизны в данной точке, т. е. радиус окружности, часть дуги которой совпадает с траекторией в данной точке.
В точке О
V = V0, a = gcos@
R0 = V0^2/gcos@
B точке А
Vy = 0, a = g, VA = V0x = V0cos@
RA = (V0^2cos@)/g
Слайд 11Приложение
Ознакомившись с основными действиями пи решении задач по теме «Движение под углом

к горизонту», Вы можете проверить приобретенные знания. С этой целью Вам предлагается следующая задача:
Слайд 12Условия задачи
Тело брошено горизонтально со скоростью 20м/с.Определить смещение тела от точки бросания,S,

при котором скорость будет направлена под углом 45’ к горизонту.
Слайд 13
Если у Вас возникли трудности при решении задачи, Вы можете воспользоваться следующими

подсказками:
1)Кратко изложенные этапы решения;
2)Необходимые формулы;
3)Ответ.
Слайд 14Этапы решения
1.Выбрать оси координат.
2.Записать уравнения движения тела.
3.Определить момент времени t, когда скорость

будет направлена под углом 45’ к горизонту.
4.Подставить t в уравнение движения и найти координаты тела.
5.Найти искомое перемещение.
Слайд 15Формулы
1.x = V0t
2.y = gt^2/2
3.Vy/Vx = tg@
4.gt = V0
5.S =

x^2 + y^2















 Презентация на тему Велосипедные походы и безопасность туристов
Презентация на тему Велосипедные походы и безопасность туристов Методы улучшения систем теплоснабжения
Методы улучшения систем теплоснабжения Хозяйство страны. 8 класс
Хозяйство страны. 8 класс Динозавр
Динозавр Значение воинского учета граждан для военной безопасности государства
Значение воинского учета граждан для военной безопасности государства Презентация на тему Царство Растения
Презентация на тему Царство Растения 44 Додаток
44 Додаток Подводный мир
Подводный мир Мультисчета в приложении
Мультисчета в приложении Лес Инвест Трейдинг
Лес Инвест Трейдинг Партнерская программа Станкин - Siemens
Партнерская программа Станкин - Siemens Игрушка Полкан
Игрушка Полкан СD DVD Blue Ray Flash как носители информации
СD DVD Blue Ray Flash как носители информации  Сыбайлас жемқорлық қылмысын жасайтын қылмыскер тұлғасы
Сыбайлас жемқорлық қылмысын жасайтын қылмыскер тұлғасы Оздоровительное и кондиционное плавание
Оздоровительное и кондиционное плавание Устное народное творчество
Устное народное творчество Презентация на тему Модели атомов. Опыт Резерфорда.
Презентация на тему Модели атомов. Опыт Резерфорда.  Презентация на тему Учим дорожные знаки
Презентация на тему Учим дорожные знаки  Тема_1_Предмет_и_социокультурные_функции_философии
Тема_1_Предмет_и_социокультурные_функции_философии Организация производства. Тема 4
Организация производства. Тема 4 Спорт в США
Спорт в США Закрепление письменных навыков сложения и вычитания в пределах 100.
Закрепление письменных навыков сложения и вычитания в пределах 100. Ж
Ж Цели урока – пример уровней оценки
Цели урока – пример уровней оценки Презентация на тему Формирование у детей дошкольного возраста навыков безопасного поведения через ознакомление с правилами доро
Презентация на тему Формирование у детей дошкольного возраста навыков безопасного поведения через ознакомление с правилами доро Инвестиционная политика авиапредприятия и инвестиционное проектирование
Инвестиционная политика авиапредприятия и инвестиционное проектирование Многообразие и значение насекомых в биоценозах
Многообразие и значение насекомых в биоценозах Страховая терминология
Страховая терминология