Эффективность параллельных вычислений

Рассматриваемые вопросы
Высокопроизводительные вычисления
Характеристики параллельности
Закон Амдаля

Высокопроизводительные вычисления
это одна из наиболее актуальных и «горячих» тем как в информационных технологиях, так и во многих прикладных областях. Причиной этого является та практическая польза, которую нельзя получить никакими другими технологиями, кроме как применением высокопроизводительных вычислений.

Под термином «высокопроизводительные вычисления»
обычно подразумевают не только выполнение большого объема расчетов, но и обработку больших объемов данных за сравнительно небольшой промежуток времени.

Как правило, о высокопроизводительных вычислениях можно говорить тогда,
когда к программно-аппаратной системе предъявляется одно или несколько из следующих требований:
- высокое быстродействие;
- наличие большого объема оперативной памяти;
- необходимость передавать большие объемы данных;
- необходимость хранить и обрабатывать большие объемы данных.

сложная задача
– это задача, которая не может быть эффективно решена на существующих массовых вычислительных средствах с помощью традиционных методов и алгоритмов решения

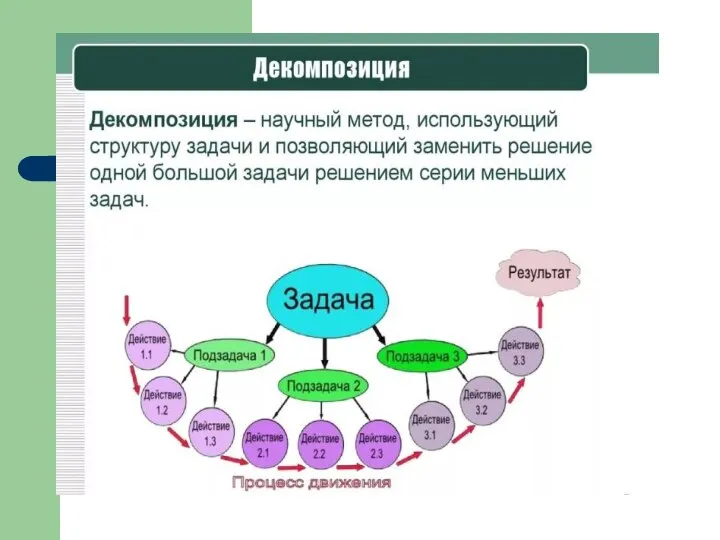
Основным подходом
к решению любой сложной задачи является декомпозиция (разбиение задачи на совокупность подзадач меньшей размерности).
З декомпозиция {З1, З2, … Зi, … Зр, Зсв},
где Зi – i-ая подзадача.
Зсв – задача связи.

Декомпозиция
разделение целого на части. Декомпозиция, как процесс расчленения, позволяет рассматривать любую исследуемую систему как сложную, состоящую из отдельных взаимосвязанных подсистем, которые, в свою очередь, также могут быть расчленены на части.

Декомпозиция

В зависимости от соотношения
трудоемкостей задачи связи и подзадач зависит, к какому классу относится исходная сложная задача З.
Принято выделять четыре основных класса сложных задач:
1. Несвязная сложная задача.
2. Слабосвязная сложная задача.
3. Среднесвязная сложная задача
4. Сильносвязная сложная задача.

Если:
1. ΣΣ Wij → 0, или T(Зсв) → 0, то З относится к классу несвязных сложных.
2. ΣΣ Wij< max T(Зi), или T(Зсв )< max T(Зi ),то З – слабосвязная задача.
3. ΣΣ Wij≅ max T(Зi), или T(Зсв )≈ max T(Зi ), то З – среднесвязная задача.
4. ΣΣ Wij> max T(Зi), или T(Зсв )> max T(Зi ), то З – сильносвязная задача.
Пусть Wij – трудоемкость обменных взаимодействий между Зi-ой и Зj-ой подзадачами в процессе решения задачи З.

По мере совершенствования МВС
происходит усложнение и увеличение количества задач в областях, традиционно использующих высокопроизводительную вычислительную технику. В настоящее время выделен круг фундаментальных и прикладных проблем, эффективное решение которых возможно только с использованием сверхмощных вычислительных ресурсов. Он включает следующие задачи:

Задачи
предсказания погоды, климата и глобальных изменений в атмосфере;
науки о материалах;
построение полупроводниковых приборов;
сверхпроводимость;
структурная биология;
разработка фармацевтических препаратов;
Генетика.

Сейсморазведка
Для повышения эффективности нефтедобычи важно знать форму и расположение нефтяного месторождения — это позволит оценить объемы извлекаемой нефти, рассчитать мощность месторождения, правильно расположить нефтяные вышки и т.д.

Данные нефтяного месторождения в Мексиканском заливе
. Площадь исследуемой поверхности составила 400 км2 , а объем собранных данных — порядка 1 Терабайта. В процессе вычислений производится около 100 миллиардов операций дискретной свертки одномерных массивов, каждый из которых состоит из 2000 элементов. Трафик данных при решении задачи составляет более одного Петабайта. Если доверить эти вычисления хоть и очень быстрому, но одному единственному, серверу, то необходимое время непрерывных круглосуточных расчетов составило бы порядка трех лет!

Распараллеливания арифметических и логических выражений
Пусть E – простое арифметическое выражение, удовлетворяющее следующему условию:
“Каждая из переменных входит в E ровно один раз”.
Выполнения этого условия всегда можно добиться переименованием переменных.
Цель любого алгоритма распараллеливания – минимизировать время, необходимое для параллельного вычисления E.

Наиболее известные алгоритмы
распараллеливания арифметических выражений Баера-Бовета, Брента и Винограда основаны на общем принципе: ориентированный ациклический граф, описывающий последовательное вычисление выражения E, представляет собой, в силу свойства , бинарное дерево.

Задача распараллеливания выражений
заключается в построении такого алгоритма, который по каждому выражению E дает эквивалентное ему Ẽ с минимальной высотой дерева вычислений.

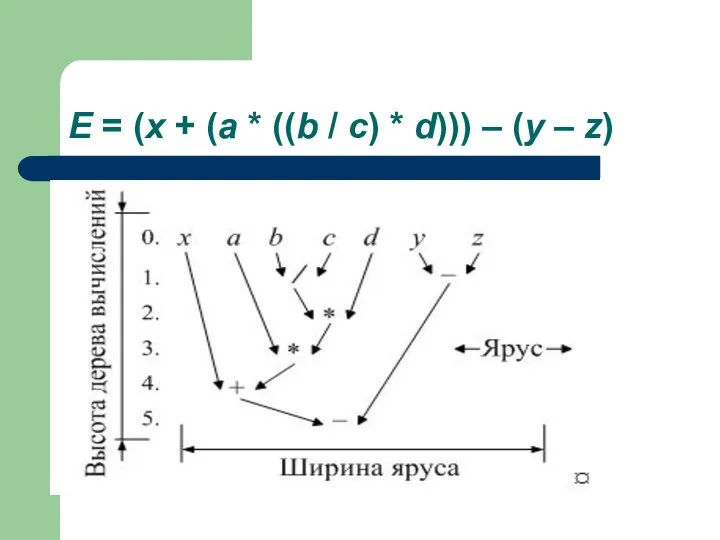
E = (x + (a * ((b / c) * d))) – (y – z)

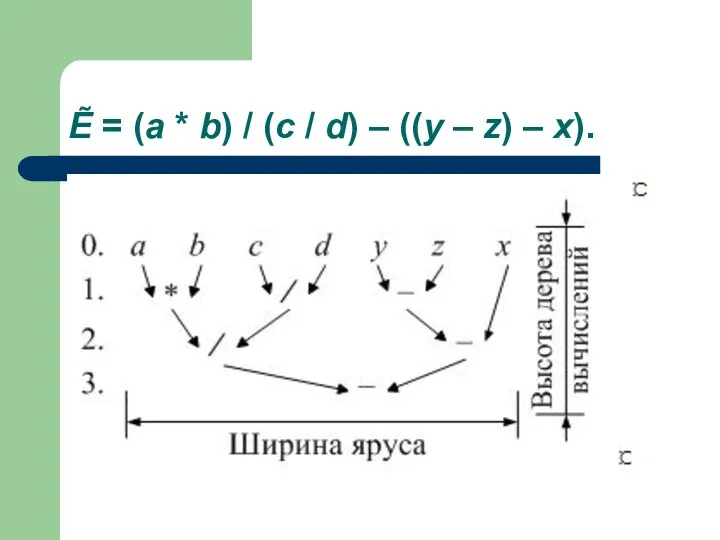
Ẽ = (a * b) / (c / d) – ((y – z) – x).

Характеристиками сложности вычисления арифметического выражения являются:
время t, затрачиваемое на вычисление арифметического выражения;
общее число операций w, необходимое для вычисления выражения;
число вычислителей (или процессоров) p, требуемое для реализации вычислений.

Если считать
, что любая операция занимает одну единицу времени, то время t вычисления арифметического выражения равно числу ярусов (высоте) дерева вычислений. Операции, лежащие на одном ярусе дерева, могут выполняться параллельно и определяют ширину данного яруса. Поэтому высота дерева соответствует числу шагов параллельного алгоритма для арифметического выражения.

Для выражений E и Ẽ имеем следующие характеристики сложности вычисления:
Для выражения E
t = 5
p = 2
w = 6
Для выражения Ẽ
t = 3
p = 3
w = 6

Для оценки
распараллеленного выражения будем использовать такие характеристики параллельности, как ускорение и эффективность параллельных алгоритмов.
Пусть n – число параметров задачи (для арифметического выражения – число различных переменных, входящих в арифметическое выражение).
Tp(n) – время выполнения параллельного алгоритма на вычислительной системе с числом процессоров p>1.
T1(n) – время выполнения “наилучшего” последовательного алгоритма.

Ускорением ξp параллельного алгоритма называют отношение ξ= T1(n) /Tр(n)
, а эффективность ξ*p параллельного алгоритма определяется по формуле
ξ*= ξ/р=T1(n) /(Tр(n)*р) .

Имеем следующие характеристики параллельных вычислений:
Для выражения E
T1(n) = n – 1 = 6
Tp(n) = t = 5
ξp (n) = 6/5 = 1.2
ξ*p(n) = 1.2/2 = 0.6
Для выражения Ẽ
T1(n) = n – 1 = 6
Tp(n) = t = 3
ξp (n) = 6/3 = 2
ξ*p(n) = 2/3 = 0.66

Еще две полезные оценки для параллельных схем вычислений являются
цена и ценность параллельного решения.
Цена параллельного решения –
Cp = p*Tp(n)
Ценность параллельного решения –
Fp = ξ/Cp = T1(n)/p*Tp2(n).

Характеристики сложности:
1. Т – трудоемкость решения задачи (часто определяется числом мультипликативных операций).
2. О – объем обрабатываемой информации.
3. t доп. – допустимое время решения задачи.
4. Р – требуемая производительность, Р = Т/t доп.

Трудоемкость решения задачи
T1(n) - трудоемкость решения некоторой задачи З(n), где n – это размерность задачи, на одном вычислителе с помощью наилучшего последовательного алгоритма.
Tр(n) – трудоемкость решения задачи З(n) на p вычислителях с использованием некоторого параллельного алгоритма.
T(Зi) – трудоемкость решения подзадачи Зi
T(Зсв) – трудоемкость решения задачи связи Зсв

Ускорение параллельного вычисления
ξ= T1(n) /Tр(n)
Чем менее связная задача, тем больше число подсистем на которые целесообразно разбивать исходные подзадачи. Чем более связная задача, тем меньше число подсистем р на которые следует разбивать исходные подзадачи. Чем ближе значение ускорения к р (ξ→ р), тем лучше параллельный алгоритм и соответствующая параллельная программа

Эффективность параллельного вычисления
ξ*= ξ/р=T1(n) /(Tр(n)*р)
Чем ближе значение ускорения к р, тем более эффективен (ξ*→1) параллельный алгоритм и соответствующая параллельная программа

Используется для оценки параллельных алгоритмов, структура которых предполагает выполнение всех операций либо с максимальной, либо с минимальной степенью параллелизма, время на подготовку передачи данных отсутствует.
Закон Амдаля

Предположим, что программе доля операций, которые нужно выполнять последовательно, равна β, где 0<= β <=1 (при этом доля понимается не по статическому числу строк кода, а по числу операций в процессе выполнения).
Крайние случаи в значениях β соответствуют полностью параллельным (β =0) и полностью последовательным (β =1) программам.
Определим ускорение параллельного алгоритма исходя из анализа частей алгоритма, выполняемых последовательно и параллельно:

Чтобы оценить, какое ускорение S может быть получено на компьютере из p процессоров при данном значении β, можно воспользоваться законом Амдала:

Закон Амдала

Проанализируем полученное соотношение:
Имеем большие затраты на обмен данными и синхронизацию, что может привести к неэффективности параллельного алгоритма.

Если 9/10 программы исполняется параллельно, а 1/10 по-прежнему последовательно, то ускорения более, чем в 10 раз получить в принципе невозможно вне зависимости от качества реализации параллельной части кода и числа используемых процессоров (ясно, что 10 получается только в том случае, когда время исполнения параллельной части равно 0).

Отсюда вывод
Если, оценив заложенный в программе алгоритм, ясно, что доля последовательных операций велика, то на значительное ускорение рассчитывать явно не приходится и нужно думать о замене отдельных компонент алгоритма.

Важнейшим классом арифметических выражений являются рекурсивные выражения
Рекурсия встречается в матричных операциях, является основой многих методов для вычисления значений функции и используется в ряде методов численного интегрирования.
При рекурсивных операциях значение каждого очередного члена последовательности или элемента структуры зависит от значений одного или нескольких предшествующих членов.

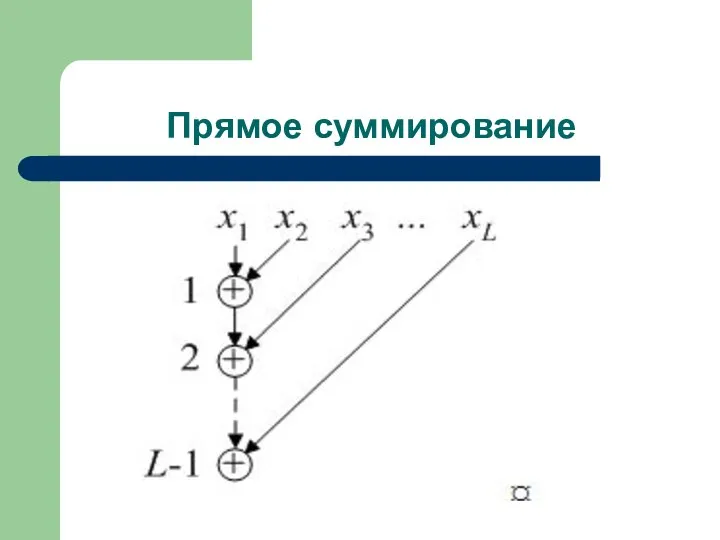
Прямое суммирование

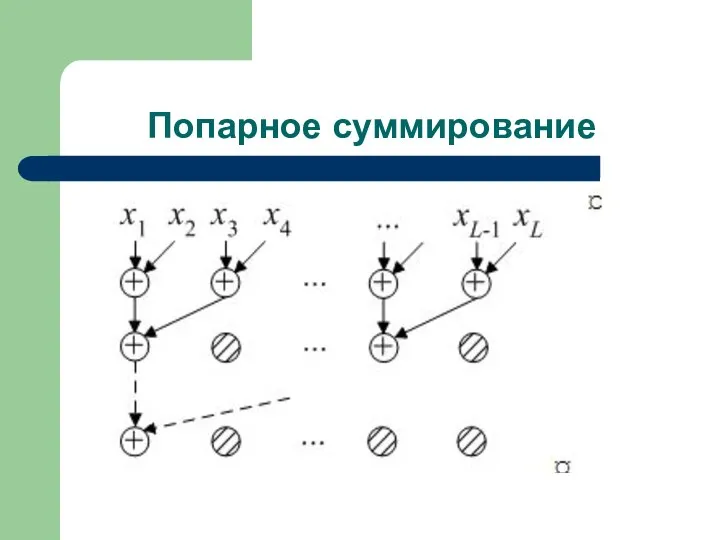
Попарное суммирование

Такой метод
нахождения суммы элементов вектора получил название метода рекурсивного сдваивания или метода нахождения параллельных каскадных сумм.

В ряде случаев последовательный характер алгоритма изменить не так сложно.
Допустим, что в программе есть следующий фрагмент для вычисления суммы n чисел:
s = 0
Do i = 1, n
s = s + a(i)
EndDo.

По своей природе
он строго последователен, так как на i-й итерации цикла требуется результат с (i-1)-й и все итерации выполняются одна за одной. Имеем 100% последовательных операций, а значит и никакого эффекта от использования параллельных компьютеров.

Вместе с тем, выход очевиден.
Поскольку в большинстве реальных программ нет существенной разницы, в каком порядке складывать числа, выберем иную схему сложения. Сначала найдем сумму пар соседних элементов: a(1)+a(2), a(3)+a(4), a(5)+a(6) и т.д. Заметим, что при такой схеме все пары можно складывать одновременно! На следующих шагах будем действовать абсолютно аналогично, получив вариант параллельного алгоритма.

требования к высокопроизводительным вычисленийям

сложная задача -это

Декомпозиция - это

Высота дерева решения равна- 5, ширина-4
Арифметического выражения включает 10 операций
Ускорение равно______

Высота дерева решения равна- 5, ширина-2
Арифметического выражения включает 10 операций
Цена параллельного решения равна______

Высота дерева решения равна- 4, ширина-3
Арифметического выражения включает 12 операций
оптимальное число процессоров равно______

Высота дерева решения равна- 3, ширина-4
Арифметического выражения включает 12 операций
эффективность равно______

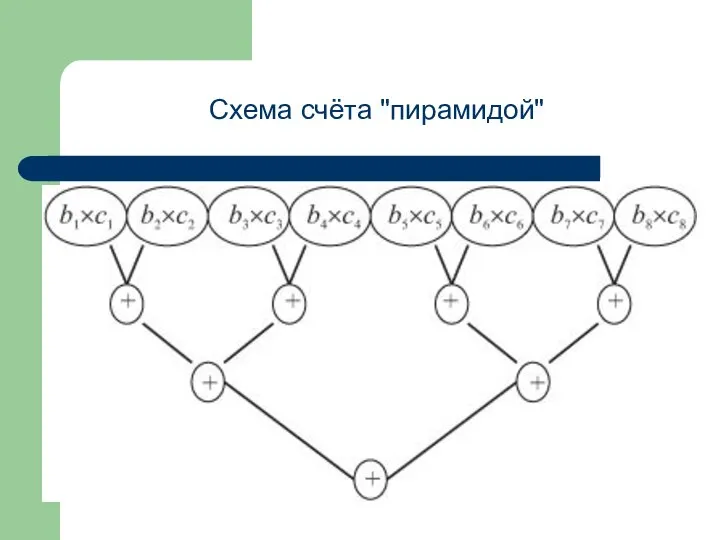
Пример
Скалярное умножение векторов заданной длины: A = B x C способом "пирамиды",
В = {b1 , ... , b8}, C = {c1 , ... , c8}.

Схема счёта "пирамидой"

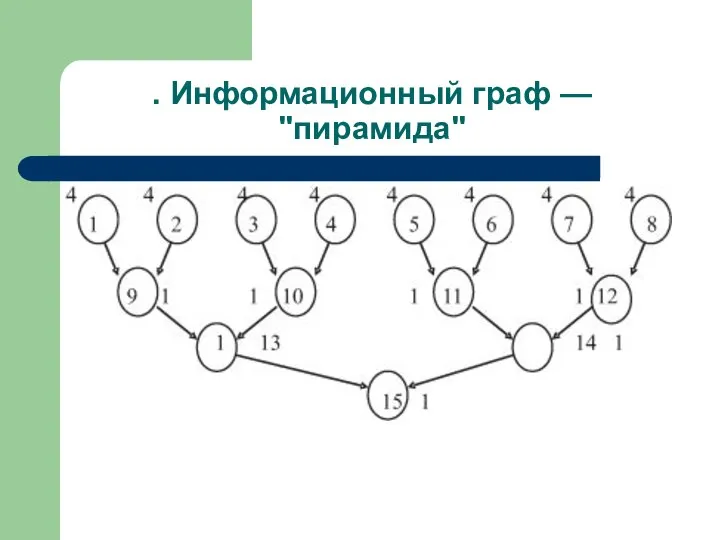
. Информационный граф — "пирамида"

Высокая производительность ВС
достигается структурными методами, основанными на параллельной обработке информации. ВС содержит несколько процессоров или операционных устройств, способных одновременно, но с необходимой синхронизацией, выполнять доли возлагаемых на них работ по реализации алгоритма решения задачи.