Содержание
- 2. В основе современной логики лежат учения, созданные ещё древнегреческими мыслителями, хотя первые учения о формах и
- 3. Алгебра логики (булева алгебра) раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или
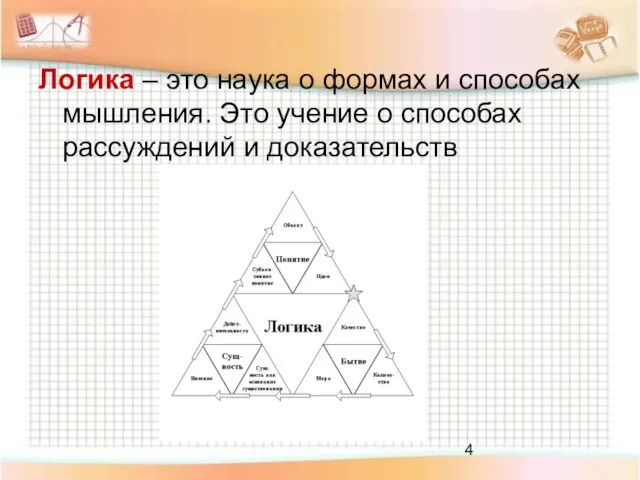
- 4. Логика – это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств
- 5. Джордж Буль
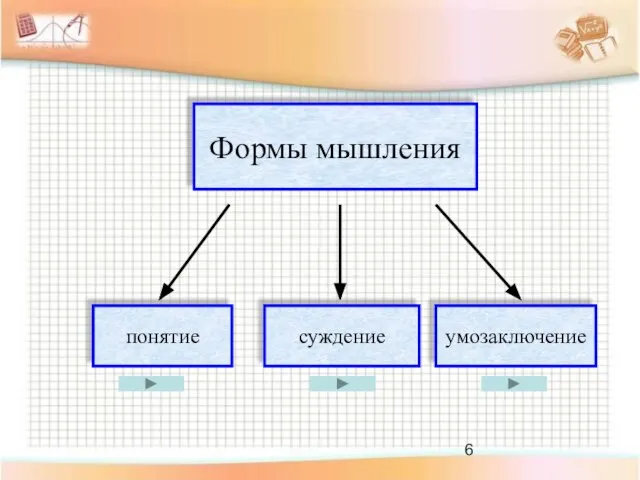
- 6. умозаключение суждение Формы мышления понятие Формы мышления понятие суждение Формы мышления понятие умозаключение суждение Формы мышления
- 7. Понятие это форма мышления, которая выделяет существенные признаки объекта, позволяющие отличать их от других Прямоугольник, проливной
- 8. Содержание – это все существенные признаки объекта или класса объектов, отраженные в понятии
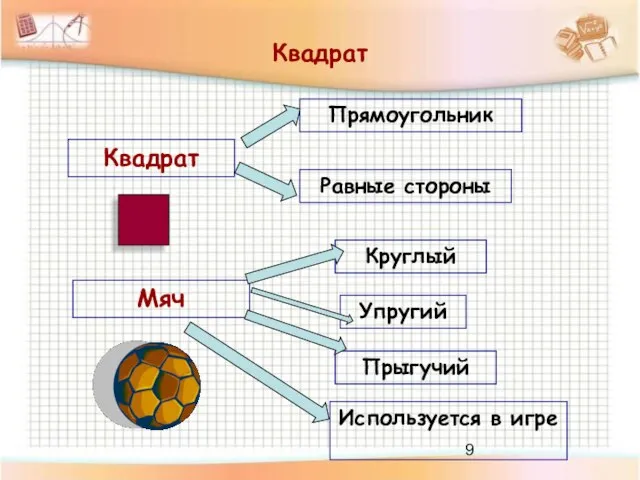
- 9. Квадрат
- 10. Объем – множество объектов, каждому из которых присущи признаки, составляющие содержание понятия
- 11. Множество отличников в классе Множество букв русского алфавита Множество натуральных чисел Множество знаков
- 12. Высказывание это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и
- 13. Логическое высказывание это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно
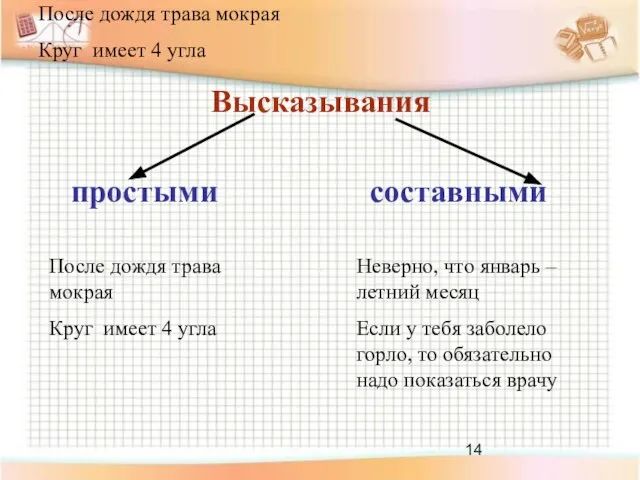
- 14. После дождя трава мокрая Круг имеет 4 угла Высказывания простыми составными После дождя трава мокрая Круг
- 15. Истинность простых высказываний определяется на основании здравого смысла Истинность составных высказываний определяется с помощью алгебры логики
- 16. Высказывания бывают общимиобщими, частными или единичными Общее высказывание начинается со слов: все, всякий, каждый, ни один
- 17. Общее высказывание соответствует множеству однородных объектов, которое иначе называется классом объектов. Каждого человека окружают объекты Исполнитель
- 18. Частное высказывание Некоторые школьники - спортсмены Не каждое животное является домашним Не все люди разговаривают на
- 19. Единичное высказывание соответствует конкретному объекту, тому самому, о котором идет речь Мой письменный стол сделан из
- 20. Суждение это форма мышления, в которой что-либо утверждается или отрицается об объектах, признаках или отношениях объектов
- 21. Москва больше Санкт-Петербурга Все мальчики любят играть в футбол Некоторые ученики нашего класса поют в школьном
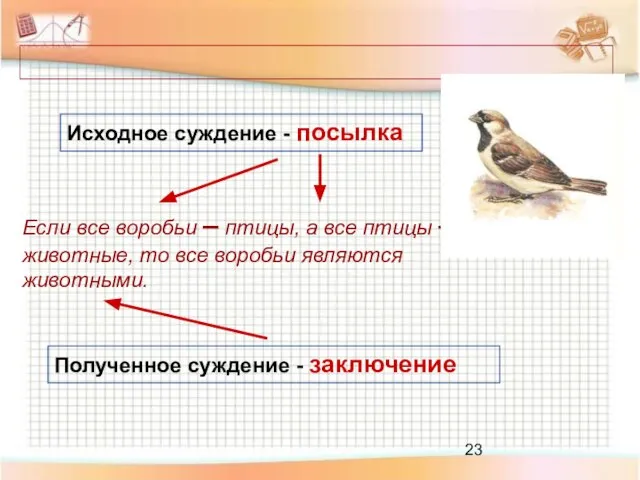
- 22. Умозаключение это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое
- 23. Исходное суждение - посылка Полученное суждение - заключение Если все воробьи – птицы, а все птицы
- 24. Алгебра высказываний Служит для определения истинности или ложности составных высказываний, не вникая в их содержание В
- 25. Записать в виде логического выражения высказывание: Летом Петя поедет в деревню и, если будет хорошая погода,
- 26. Операции над логическими высказываниями
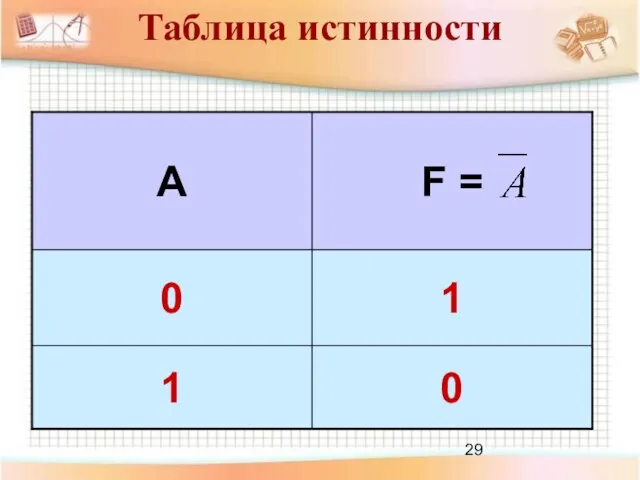
- 27. Инверсия Логическое отрицание Присоединение частицы «не» к высказыванию Правило истинности: Логическое отрицание (инверсия) истинно, если высказывание
- 28. А = «Земля — планета Солнечной системы» А = «Земля — не является планетой Солнечной системы»
- 29. Таблица истинности
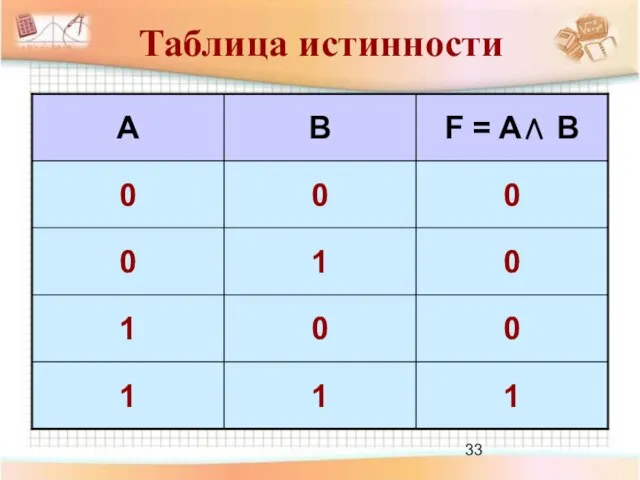
- 30. Конъюнкция Логическое умножение Объединение двух (или нескольких) высказываний в одно с помощью союза «и» Правило истинности:
- 31. «10 делится на 2 и 5 больше 3» истинно «10 делится на 2 и 5 не
- 32. Обозначение операции логического умножения: &, *, A и B – простые высказывания Конъюнкция: F = A
- 33. Таблица истинности
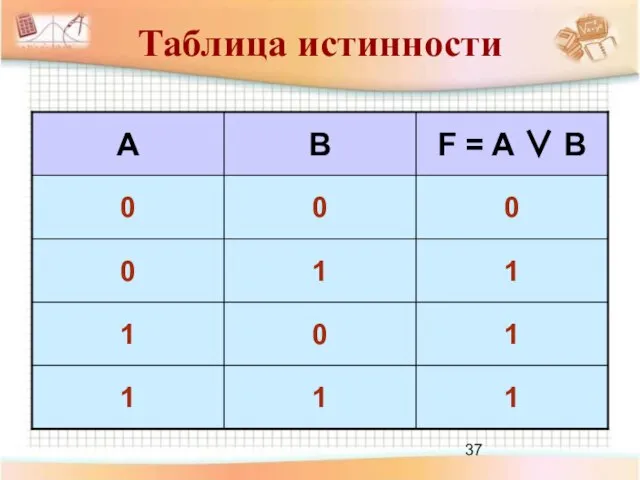
- 34. Дизъюнкция Логическое сложение Объединение двух (или нескольких) высказываний в одно с помощью союза «или» Правило истинности:
- 35. «10 не делится на 2 или 5 не больше 3» ложно «10 делится на 2 или
- 36. Обозначение операции логического сложения: ∨, + A и B – простые высказывания Дизъюнкция: F = A
- 37. Таблица истинности
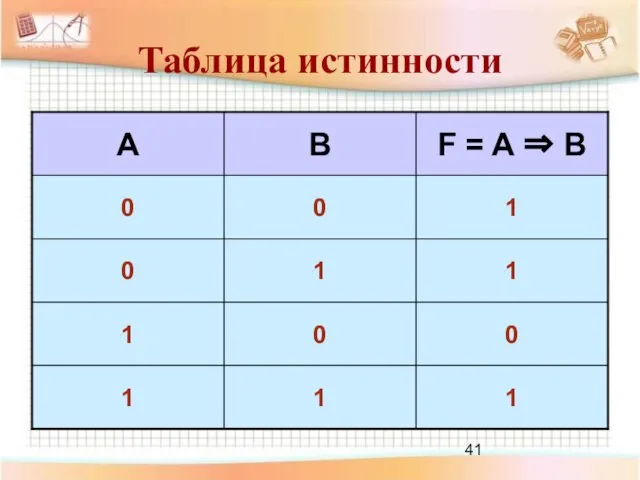
- 38. Импликация Логическое следование Соединение двух высказываний в одно с помощью оборота речи «если…, то…» Правило истинности:
- 39. «Если 10 не делится на 2, то 5 не больше 3» истинно «Если 10 делится на
- 40. Обозначение операции логического следования: ⇒ A и B – простые высказывания Импликация: F = A B
- 41. Таблица истинности
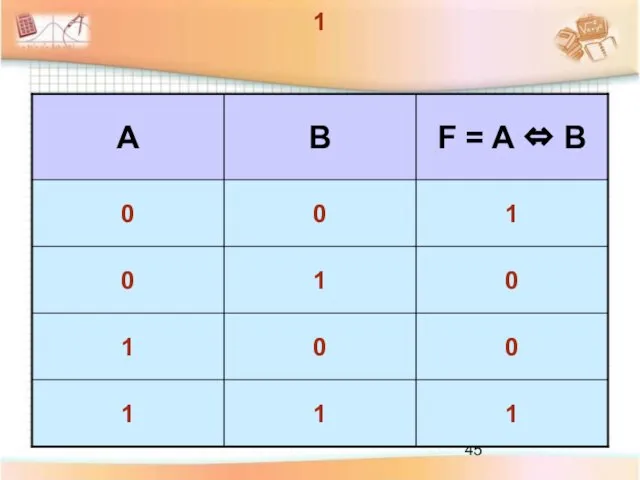
- 42. Эквивалентность Логическое равенство Соединение двух высказываний в одно помощью оборота речи «тогда и только тогда, когда»
- 43. «Если 10 не делится на 2, то 5 не больше 3» истинно «Если 10 делится на
- 44. Обозначение операции логического равносильности: ~ A и B – простые высказывания Эквивалентность: F = A B
- 45. 1
- 46. Приоритет действий Инверсия Конъюнкция Дизъюнкция Составление таблиц истинности Число строк: 2n (n – число логических переменных)
- 47. Законы логики
- 48. Закон тождества всякое высказывание тождественно самому себе
- 49. Закон непротиворечия высказывание не может быть одновременно истинным и ложным
- 50. Закон исключения третьего высказывание может быть либо истинным, либо ложным третьего не дано
- 51. Закон двойного отрицания если дважды отрицать одно и то же высказывание, то в результате получится исходное
- 52. Закон поглощения 0
- 53. Закон поглощения 1
- 54. Закон поглощения
- 55. Закон идемпотентности
- 56. Законы Моргана
- 58. Закон ассоциативности
- 59. Закон дистрибутивности
- 60. Закон коммутативности
- 63. Скачать презентацию













































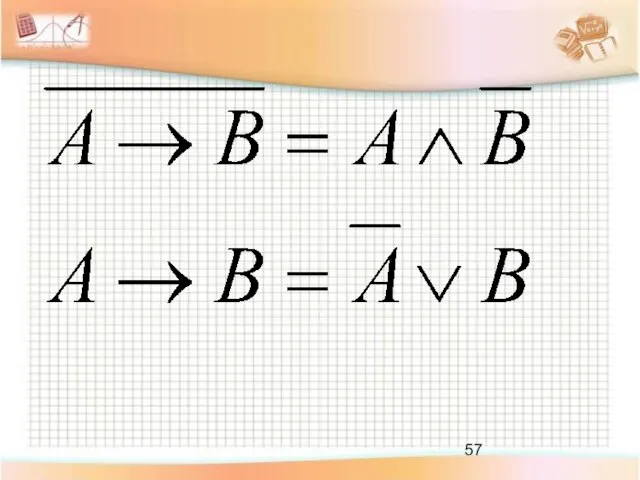



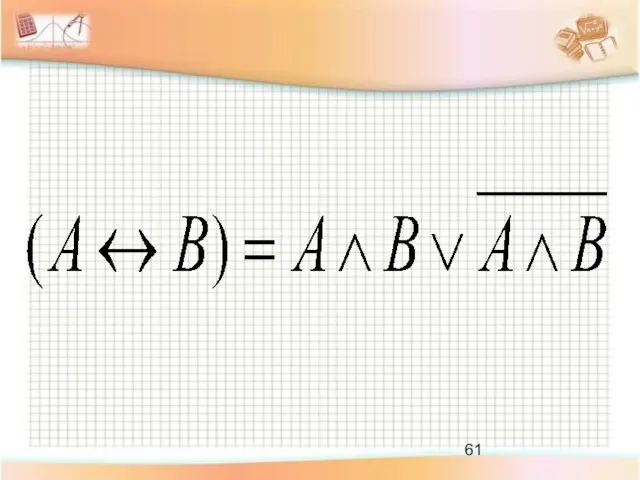
 капсула «pH-агент»
капсула «pH-агент» Космонавтика требует нового понимания гравитации и новой механики
Космонавтика требует нового понимания гравитации и новой механики Александр Николаевич Островский
Александр Николаевич Островский ЕСЛИ УЧЕНИК В ШКОЛЕ НЕ НАУЧИТСЯ САМ ТВОРИТЬ, ТО И В ЖИЗНИ ОН ВСЕГДА БУДЕТ ТОЛЬКО ПОДРАЖАТЬ, КОПИРОВАТЬ. Л.Н. Толстой
ЕСЛИ УЧЕНИК В ШКОЛЕ НЕ НАУЧИТСЯ САМ ТВОРИТЬ, ТО И В ЖИЗНИ ОН ВСЕГДА БУДЕТ ТОЛЬКО ПОДРАЖАТЬ, КОПИРОВАТЬ. Л.Н. Толстой Стилистика образа в одежде
Стилистика образа в одежде ОПЫТ РАЗРАБОТКИ ДОКУМЕНТАЦИИ СЗПДн. МОДЕЛЬ УГРОЗ БЕЗОПАСНОСТИ ПДн.
ОПЫТ РАЗРАБОТКИ ДОКУМЕНТАЦИИ СЗПДн. МОДЕЛЬ УГРОЗ БЕЗОПАСНОСТИ ПДн. Презентация на тему Знаки химических элементов
Презентация на тему Знаки химических элементов Государственное дошкольное образовательное учреждение комбинированного вида детский сад № 128 Невского района
Государственное дошкольное образовательное учреждение комбинированного вида детский сад № 128 Невского района Информационные технологии в истории
Информационные технологии в истории Математика и Древний Египет
Математика и Древний Египет Опыт реальных проектов
Опыт реальных проектов Паспорт территории села Онгурен Ольхонского района Иркутской области
Паспорт территории села Онгурен Ольхонского района Иркутской области Пищевые цепи
Пищевые цепи В гостях у минуток
В гостях у минуток Формировать понятий о растениях в экологическом образовании у детей дошкольного возраста
Формировать понятий о растениях в экологическом образовании у детей дошкольного возраста Изобретательство и авторское право
Изобретательство и авторское право маркетинговые коммуникации
маркетинговые коммуникации  Коррекционная работа с агрессивными детьми старшего дошкольного возраста
Коррекционная работа с агрессивными детьми старшего дошкольного возраста На кого же я похожа? (2 класс)
На кого же я похожа? (2 класс) Подвеска зонтик из цветной бумаги
Подвеска зонтик из цветной бумаги Синтетическая радуга
Синтетическая радуга ОСиЭНО презентация
ОСиЭНО презентация Презентация по геометрии
Презентация по геометрии Кто будет начальником
Кто будет начальником Современный характер управленческих процессов
Современный характер управленческих процессов 1,4 класс
1,4 класс Электрическое поле в вакууме
Электрическое поле в вакууме Профессиональная деятельность учителя химии и биологии МОУ СОШ № 17 г. Йошкар – Олы РМЭ Поповой Людмилы Алексеевны
Профессиональная деятельность учителя химии и биологии МОУ СОШ № 17 г. Йошкар – Олы РМЭ Поповой Людмилы Алексеевны