Эволюция механики

ПРЕДИСЛОВИЕ…
История механики, так же как и у ДРУГИХ наук, неразрывно связана с историей развития общества, с общей историей развития его производительных сил. И у каждой эпохи развития человечества, от древнего мира и вплоть до новейшего времени, стояли собственные проблемы науки и собственные пути их разрешения.

ВОЗНИКНОВЕНИЕ МЕХАНИКИ
Механика не возникла спонтанно. Это результат трудов и открытий, совершенствования технологий и строительства. Основные законы современной механики родились в результате опыта поколений, начиная с появления орудий труда и первых построек.
Родиной первой механики по праву считают древнюю Грецию, где огромными темпами развивались точные науки и строительство. Именно здесь впервые зародился важнейший раздел механики – статика. Этот раздел развивался в тесной связи со строительным искусством античного мира.

Механика античности
Основное понятие механики– понятие силы – появившееся впервые в античном мире, вначале тесно связывалось с мускульным усилием, вызванным давлением предмета на руку.
Примерно к началу IV в. до н. э. Греции уже были известны простейшие законы сложения и уравновешивания сил, приложенных к одной точке вдоль одной и той же прямой.
Особый интерес привлекала задача о рычаге. Теория рычага была создана великим ученым древности Архимедом (III в. до н. э.) и изложена в сочинении “О рычагах”.

АРХИМЕД
АРХИМЕД ( (около 287 до н.э. — 212 до н.э.), древнегреческий ученый, математик и механик, основоположник теоретической механики и гидростатики. Разработал предвосхитившие интегральное исчисление методы нахождения площадей, поверхностей и объемов различных фигур и тел. В основополагающих трудах по статике и гидростатике (закон Архимеда) дал образцы применения математики в естествознании и технике. Архимеду принадлежит множество технических изобретений (архимедов винт, определение состава сплавов взвешиванием в воде, системы для поднятия больших тяжестей, военные метательные машины), завоевавших ему необычайную популярность среди современников. Им впервые был введен закон о погруженном в жидкость теле, который сейчас известен каждому школьнику.(рис.справа, где F-выталкивающая сила, а P-сила тяжести)

МЕХАНИКА В ЭПОХУ ВОЗРОЖДЕНИЯ
С развитием ремесел, торговли, мореплавания и военного дела и связанного с ними накопления новых знаний, в XIV и XV вв. – в эпоху Возрождения – начинается расцвет наук и искусств. Крупным событием, революционизировавшим человеческое мировоззрение, явилось создание великим польским астрономом Николаем Коперником (1473 – 1543)учения о гелиоцентрической системе мира, в которой шарообразная Земля занимает центральное неподвижное положение, а вокруг нее по своим круговым орбитам движутся небесные тела: Луна, Меркурий, Венера, Солнце, Марс, Юпитер, Сатурн.
Кинематические и динамические исследования эпохи Возрождения были обращены, главным образом, на уточнение представлений о неравномерном и криволинейном движении точки. До этого времени общепринятыми были не соответствующие действительности динамические воззрения Аристотеля, изложенные в его “Проблемах механики”.

ЛЕОНАРДО ДА ВИНЧИ – РИСУНКИ ГЕНИЯ
Леонардо да Винчи (1452-1519) титан Возрождения, ученый и живописец, внесший огромный вклад в технику, естественные и точные науки. Особое внимание Леонардо уделял механике, называя ее «раем математических наук» и видя в ней ключ к тайнам мироздания; он попытался определить коэффициенты трения скольжения, изучал сопротивление материалов, увлеченно занимался гидравликой. Многочисленные гидротехнические эксперименты получили выражение в новаторских проектах каналов и ирригационных систем. Страсть к моделированию приводила Леонардо к поразительным техническим предвидениям, намного опережавшим эпоху: таковы наброски проектов металлургических печей и прокатных станов, ткацких станков, печатных, деревообрабатывающих и прочих машин, подводной лодки и танка, а также разработанные после тщательного изучения полета птиц конструкции летальных аппаратов и парашюта.

РИСУНКИ, ОПЕРЕДИВШИЕ ЭПОХУ
Рисунки и чертежи Леонардо – результат его многочисленных исследований в анатомии и механике. Зарисовки «вечного двигателя», плечо силы под видом «потенциального рычага», механические птицы….все то, что во времена да Винчи считалось непостижимым, теперь реальность. Ученый смотрел далеко вперед и его открытия в технике и механике до сих пор считаются феноменальными.

Галилео Галилей
ГАЛИЛЕЙ Галилео (1564-1642), итальянский ученый, один из основателей точного естествознания. Боролся против схоластики, считал основой познания опыт. Заложил основы современной механики: выдвинул идею об относительности движения, установил законы инерции, свободного падения и движения тел по наклонной плоскости, сложения движений; открыл изохронность колебаний маятника; первым исследовал прочность балок

Открытия Галилея в механике
Галилей экспериментально установил количественный закон падения тел в пустоте, согласно которому расстояния, проходимые падающим телом в одинаковые промежутки времени, относятся между собой, как последовательные нечетные числа.
Галилей установил законы движения тяжелых тел по наклонной плоскости, показав, что, падают ли тяжелые тела по вертикали или по наклонной плоскости, они всегда приобретают такие скорости, которые нужно сообщить им, чтобы поднять их на ту высоту, с которой они упали. Переходя к пределу, он показал, что на горизонтальной плоскости тяжелое тело будет находиться в покое или будет двигаться равномерно и прямолинейно

Складывая горизонтальное и вертикальное движения тела (это первое в истории механики сложение конечных независимых движений), он доказал, что тело, брошенное под углом к горизонту, описывает параболу, и показал, как рассчитать длину полета и максимальную высоту траектории
В диалогах о двух системах мира очень образно, в форме художественного описания, он показал, что все движения, которые могут происходить в каюте корабля, не зависят от того, находится ли корабль в покое или движется прямолинейно и равномерно. Этим он установил принцип относительности классической механики (так называемый принцип относительности Галилей – Ньютона)
Исследуя условия равновесия простых машин и плавания тел, Галилей, по существу, применяет принцип возможных перемещений (правда, в зачаточной форме). Ему же наука обязана первым исследованием прочности балок и сопротивления жидкости движущимся в ней телам.

Опыты Галилея
Галилей впервые выяснил, что тяжелые предметы падают вниз так же быстро, как и легкие. Чтобы проверить это предположение Галилео Галилей сбрасывал с Пизанской башни в один и тот же момент пушечное ядро массой 80 кг и значительно более легкую мушкетную пулю массой 200 г. Оба тела имели примерно одинаковую обтекаемую форму и достигли земли одновременно. До него господствовала точка зрения Аристотеля, который утверждал, что легкие тела падают с высоты медленнее тяжелых.

Галилей использовал наклонную плоскость с гладкой канавкой посередине, по которой скатывались латунные шары. По водным часам он засекал определённый интервал времени и фиксировал расстояния, которые за это время преодолевали шары. Галилей выяснил, что если время увеличить в два раза, то шары прокатятся в четыре раза дальше (т.е. зависимость квадратичная). Это опровергало мнение Аристотеля, что скорость шаров будет постоянной.

Открытия Рене Декарта
Французский геометр и философ Р. Декарт (1596 – 1650) высказал плодотворную идею сохранения количества движения. Он применяет математику к анализу движения и, вводя в нее переменные величины, устанавливает соответствие между геометрическими образами и алгебраическими уравнениями. Но он не заметил существенного факта, что количество движения является величиной направленной, и складывал количества движения арифметически. Это привело его к ошибочным выводам и снизило значение данных им применений закона сохранения количества движения, в частности, к теории удара тел.

Физический маятник Гюйгенса
Последователем Галилея в области механики был голландский ученый Х. Гюйгенс (1629 – 1695). Ему принадлежит дальнейшее развитие понятий ускорения при криволинейном движении точки (центростремительное ускорение). Гюйгенс также решил ряд важнейших задач динамики – движение тела по кругу, колебания физического маятника, законы упругого удара. Он первый сформулировал понятия центростремительной и центробежной силы, момента инерции, центра колебания физического маятника. Но основная его заслуга состоит в том, что он первый применил принцип, по существу эквивалентный принципу живых сил (центр тяжести физического маятника может подняться только на высоту, равную глубине его падения). Пользуясь этим принципом, Гюйгенс решил задачу о центре колебания маятника – первую задачу динамики системы материальных точек. Исходя из идеи сохранения количества движения, он создал полную теорию удара упругих шаров.

Исаак Ньютон (1643–1727) основатель классической механики
Исаак Ньютон, английский математик, механик, астроном и физик, создатель классической механики, член (1672) и президент (с 1703) Лондонского королевского общества. Фундаментальные труды «Математические начала натуральной философии» (1687) и «Оптика» (1704). Разработал (независимо от Г. Лейбница) дифференциальное и интегральное исчисления. Открыл дисперсию света, хроматическую аберрацию, исследовал интерференцию и дифракцию, развивал корпускулярную теорию света, высказал гипотезу, сочетавшую корпускулярные и волновые представления. Построил зеркальный телескоп. Сформулировал основные законы классической механики. Открыл закон всемирного тяготения, дал теорию движения небесных тел, создав основы небесной механики. Пространство и время считал абсолютными. Работы Ньютона намного опередили общий научный уровень его времени, были малопонятны современникам.

Закон всемирного тяготения
Сила F взаимного притяжения материальных точек с массами m1 и m2 находящихся на расстоянии r друг от друга, равна:
F = Gm1 m2/ r2, где G — гравитационная постоянная.

ПЕРВЫЙ ЗАКОН НЬЮТОНА
Существуют такие системы отсчета (называемые инерциальными), относительно которых любое тело, не взаимодействующее с другими телами, движется равномерно и прямолинейно

ВТОРОЙ ЗАКОН НЬЮТОНА
Если масса тела постоянная (m = const), то сила равна произведению массы тела на ускорение:
F = ma
В общем случае сила равна производной от импульса тела постоянной массы m по времени:
F = (mv)’ = d(mv)/dt

ТРЕТИЙ ЗАКОН НЬЮТОНА
Два тела действуют друг на друга с силами, равными по модулю и направленными вдоль одной прямой в противоположных направлениях:
F = - F
12
21

ТАКИМ ОБРАЗОМ, ПЕРВЫЙ ЗАКОН НЬЮТОНА УСТАНАВЛИВАЕТ СУЩЕСТВОВАНИЕ ИНЕРЦИАЛЬНЫХ СИСТЕМ ОТСЧЕТА, ВТОРОЙ И ТРЕТИЙ ЗАКОНЫ НЬЮТОНА ВЫПОЛНЯЮТСЯ ТОЛЬКО В ЭТИХ СИСТЕМАХ ОТСЧЕТА. ЭТИ ЗАКОНЫ НЕ ПРИМЕНИМЫ ДЛЯ ДВИЖЕНИЯ ОБЪЕКТОВ ОЧЕНЬ МАЛЫХ РАЗМЕРОВ, КАК АТОМЫ, И ПРИ ДВИЖЕНИЯХ СО СКОРОСТЯМИ БЛИЗКИМИ К СКОРОСТЯМ СВЕТА.

РАЗВИТИЕ МЕХАНИКИ В XVIII ВЕКЕ
К концу XVII в. основы механики были обстоятельно разработаны. Если древние века считать предысторией механики, то XVII в. можно рассматривать как период создания ее основ.
Развитие методов механики в XVIII в.. В XVIII в. потребности производства – необходимость изучения важнейших механизмов, с одной стороны, и проблема движения Земли и Луны, выдвинутая развитием небесной механики, с другой, - привели к созданию общих приемов решения задач механики материальной точки, системы точек твердого тела, развитых в “Аналитической механике” (1788 г.) Ж. Лагранжа (1736 – 1813
Ж.Ланграж

Динамика Эйлера (1707-1783)
ЭЙЛЕР Леонард (1707-83), математик, механик, физик и астроном. По происхождению швейцарец. В 1726 был приглашен в Петербургскую АН и переехал в 1727 в Россию. Был адъюнктом (1726), а в 1731-41 и с 1766 академиком Петербургской АН (в 1742-66 иностранный почетный член). В 1741-66 работал в Берлине, член Берлинской АН. Эйлер — ученый необычайной широты интересов и творческой продуктивности. Автор св. 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике.
Л.Эйлер

Л. Эйлер - основоположник механики твердого тела. Ему принадлежит общепринятый метод кинематического описания движения твердого тела при помощи трех эйлеровых углов. Фундаментальную роль в дальнейшем развитии динамики и многих ее технических приложений сыграли установленные Эйлером основные дифференциальные уравнения вращательного движения твердого тела вокруг неподвижного центра. Эйлер установил два интеграла: интеграл момента количеств движения
A2w2x + B2w2y + C2w2z = m
и интеграл живых сил (интеграл энергии)
Aw2x + Bw2y + Cw2z = h,
где m и h – произвольные постоянные, A,B и C – главные моменты инерции тела для неподвижной точки, а wx, wy, wz – проекции угловой скорости тела на главные оси инерции тела.
Эти уравнения явились аналитическим выражением открытой им теоремы моментов количества движения, которая представляет собой необходимое дополнение к закону количестве движения, сформулированному в общем виде в “Началах” Ньютона .

Эти уравнения явились аналитическим выражением открытой им теоремы моментов количества движения, которая представляет собой необходимое дополнение к закону количестве движения, сформулированному в общем виде в “Началах” Ньютона. В “Механике” Эйлера дана близкая к современной формулировка закона “живых сил” для случая прямолинейного движения и отмечено наличие таких движений материальной точки, при которых изменение живой силы при переходе точки из одного положения в другое не зависит от формы траектории. Этим было положено начало понятия потенциальной энергии. Эйлер – основоположник гидромеханики. Им были даны основные уравнения динамики идеальной жидкости; ему принадлежит заслуга создания основ теории корабля и теории устойчивости упругих стержней; Эйлер заложил основу теории расчета турбин, выведя турбинное уравнение; в прикладной механике имя Эйлера связано с вопросами кинематики фигурных колес, расчета трения между канатом и шкивом и многими другими.

Развитие механики во второй половине XVIII века.
Одним из важнейших приложений ньютоновской теории тяготения явился вопрос о фигурах равновесия вращающихся жидких масс, частицы которых тяготеют друг к другу, в частности о фигуре Земли. Основы теории равновесия вращающихся масс были изложены Ньютоном в третьей книге “Начал”. Проблема фигур равновесия и устойчивости вращающейся жидкой массы сыграла значительную роль в развитии механики во второй половине XVIII в.

Открытия Ломоносова
Великий русский ученый М. В. Ломоносов (1711 – 1765) высоко оценивал значение механики для естествознания, физики и философии. Ему принадлежит материалистическая трактовка процессов взаимодействия двух тел: “когда одно тело ускоряет движение другого и сообщает ему часть своего движения, то только так, что само теряет такую же часть движения”. Он является одним из основоположников кинетической теории теплоты и газов, автором закона сохранения энергии и движения. Приведем слова Ломоносова из письма Эйлеру (1748 г.): “Все изменения, случающиеся в природе, проходят так, что если что-либо прибавится к чему-либо, то столько же отнимется от чего-то другого. Так, сколько к какому-нибудь телу присоединится материи, столько же отнимется. Ломоносов впервые предсказал существование абсолютного нуля температуры, высказал мысль о связи электрических и световых явлений. В результате деятельности Ломоносова и Эйлера появились первые труды русских ученых, творчески овладевших методами механики и способствовавших ее дальнейшему развитию.
М.Ломоносов

Принципы динамики несвободной системы
История создания динамики несвободной системы связана с развитием принципа возможных перемещений, выражающим общие условия равновесия системы. Этот принцип был впервые применен голландским ученым С. Стевином (1548 – 1620) при рассмотрении равновесия блока. Галилей сформулировал принцип в виде “золотого правила” механики, согласно которому “что выигрывается в силе, то теряется в скорости”. Современная формулировка принципа была дана в конце XVIII в. на основе абстракции “идеальных связей”, отражающих представление об “идеальной” машине, лишенной внутренних потерь на вредные сопротивления в передаточном механизме. Выглядит она следующим образом: если в положении изолированного равновесия консервативной системы со стационарными связями потенциальная энергия имеет минимум, то это положение равновесия устойчиво.

Созданию принципов динамики несвободной системы способствовала задача о движении несвободной материальной точки. Материальная точка называется несвободной, если она не может занимать произвольного положения в пространстве. В этом случае принцип Д’Аламбера звучит следующим образом: действующие на движущуюся материальную точку активные силы и реакции связей можно в любой момент времени уравновесить добавлением к ним силы инерции.

Жозеф Луи Лагранж (1736-1813)
Французский математик и механик, иностранный почетный член Петербургской АН (1776).
Автор трудов по вариационному исчислению, где им разработаны основные понятия и методы, математическому анализу, теории чисел, алгебре, дифференциальным уравнениям. В трактате «Аналитическая механика» (1788) в основу статики положил принцип возможных перемещений, в основу динамики — сочетание этого принципа с принципом Д'Аламбера (принцип Д'Аламбера — Лагранжа), придал уравнениям движения формулу, названную его именем. Уравнение Лагранжа используется в гидродинамике и общей механике. Его сочинения по математике, астрономии и механике составляют 14 томов.

Формула конечных приращений Лагранжа
формула дифференциального исчисления; дает связь между приращением функции f( х) и значениями ее производной:
f( b)-f( a)=( b- a)f'( c)

Итоги развития механики в XVIII веке
Аналитическая механика” Лагранжа подвела итог достижениям теоретической механики XVIII в. и определила следующие главные направления ее развития:
1) расширение понятия связей и обобщение основных уравнений динамики несвободной системы для новых видов связей;
2) формулировка вариационных принципов динамики и принципа сохранения механической энергии;
3) разработка методов интегрирования уравнений динамики.

Основные открытия в механике XIX и начала XX вв.
В середине XIX в. был сформулирован принцип сохранения энергии: для любой физической системы можно определить величину, называемую энергией и равную сумме кинетической, потенциальной, электрической и других энергий и теплоты, значение которой остается постоянным независимо от того, какие изменения происходят в системе
Значительно ускорившийся к началу XIX в. процесс создания новых машин и стремление к дальнейшему их усовершенствованию вызвали в первой четверти века появление прикладной, или технической, механики
В середине XVIII в. возникли, и в XIX в. получили развитие новые общие принципы динамики – вариационные принципы.
В XIX и начале XIX вв. были заложены основы двух важных разделов гидродинамики: динамики вязкой жидкости и газовой динамики.

Основные проблемы механики XIX-XX века.
Крупнейшими проблемами динамики, постановка и решение которых относятся, главным образом, к XIX в., являются: движение тяжелого твердого тела, теория упругости, равновесия и движения, а также тесно связанная с этой теорией задача о колебаниях материальной системы.

М.В.Остроградский (1801-1861)
Российский математик и механик, академик Петербургской АН (1830),Остроградский сформулировал общий вариационный принцип для неконсервативных систем. Труды по математическому анализу, математической физике, аналитической и небесной механике, гидромеханике, теории упругости, баллистике

Открытия Остроградского в области механики
Он первый рассмотрел связи, зависящие от времени, ввел новое понятие о неудерживающих связях, т. е. связях, выражающихся аналитически при помощи неравенств, и обобщил на случай такого рода связей принцип возможных перемещений и общее уравнение динамики.
Остроградскому принадлежит также приоритет в рассмотрении дифференциальных связей, накладывающих ограничения на скорости точек системы; аналитически такие связи выражаются при помощи неинтегрируемых дифференциальных равенств или неравенств.
Предложил приложение к принципу Д’Аламбера, к системам подверженным действию мгновенных и импульсных сил, возникающих при действии на систему ударов.

Открытия Кирхгофа (1824-1887)
Один из создателей спектрального анализа, Густав Кирхгоф стал автором метода расчета токов в разветвленных электрических цепях, был одним из крупнейших физиков и педагогов конца 19 века. Член Берлинской АН (1874), член-корреспондент Петербургской АН (1862). Кирхгофом были предложены основы теории движения твердого тела в идеальной жидкости в 1869 году. Кроме механических открытий, он сформулировал один из важнейших законов о тепловом излучении и ввел понятие абсолютной черной дыры (рисунок справа).Его «Лекции по математической физике» сыграли большую роль в развитии теоретической физики.

Эксперимент Жана-Бернара Фуко (1819-1868)
Эксперимент Жана-Бернара-Леона Фуко, проведённый в 1851 году. Французский физик экспериментально доказал вращение Земли вокруг оси с помощью 67-метрового маятника, подвешенного к вершине купола парижского Пантеона. Подобный маятник до недавнего времени можно было увидеть в Петербурге в Исаакиевском соборе.

Колебания маятника Фуко зависит от того, как они были возбуждены. Если маятник отклонить на максимальный угол, а затем отпустить его без начальной скорости , то маятник будет колебаться, как изображено на верхней анимации. Скорость движения маятника в положении максимального отклонения будет равна нулю
Несколько иной характер траектории получится, если маятник приводится в движение коротким толчком из положения равновесия. Этому случаю соответствует нижняя анимация. Скорость маятника в положении максимального отклонения соответствует скорости вращения Земли на широте наблюдения.

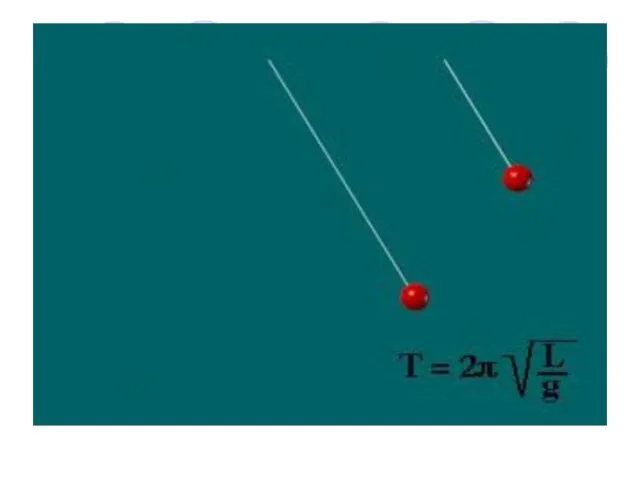
Опыт с математическим маятником
Математический маятник — материальная точка, совершающая под действием силы тяжести колебательные движения. Приближенно такой маятник может быть осуществлен в виде тяжелого груза достаточно малых размеров, подвешенного на нити.

Одной из важнейших проблем механики является задача об устойчивости равновесия и движения материальных систем. Первая общая теорема об устойчивости равновесия системы, находящейся под действием обобщенных сил, принадлежит Лагранжу и изложена в “Аналитической механике”. Согласно этой теореме, достаточным условием равновесия является наличие в положении равновесия минимума потенциальной энергии. Метод малых колебаний, примененный Лагранжем для доказательства теоремы об устойчивости равновесия, оказался плодотворным для исследования устойчивости установившихся движений. В “Трактате об устойчивости заданного состояния движения” английского ученого Э. Рауса, опубликованном в 1877 г., исследование устойчивости методом малых колебаний было сведено к рассмотрению распределения корней некоторого “характеристического” уравнения и указаны необходимые и достаточные условия, при которых эти корни имеют отрицательные вещественные части.

Механика в России и СССР
. Механика в дореволюционной России, благодаря плодотворной научной деятельности М. В. Остроградского, Н. Е. Жуковского, С. А. Чаплыгина, А. М. Ляпунова, А. Н. Крылова и других, достигла больших успехов и оказалась в состоянии не только справиться с задачами, выдвинутыми перед ней отечественной техникой, но и способствовать развитию техники во всем мире. Трудами “отца русской авиации” Н. Е. Жуковского были заложены основы аэродинамики и авиационной науки в целом. Работы Н. Е. Жуковского и С. А. Чаплыгина имели основное значение в развитии современной гидроаэромеханики. С. А. Чаплыгину принадлежит фундаментальное исследование в области газовой динамики, указавшее на многие десятки лет вперед пути развития аэродинамики больших скоростей. Работы А. Н. Крылова по теории устойчивости качки корабля на волнении, исследования по вопросам плавучести их корпуса, теория девиации компасов поставили его в ряд основоположников современной науки о кораблестроении.

Российский ученый, основоположник современной аэродинамики, член-корреспондент РАН (1917; член-корреспондент Петербургской АН с 1894). Труды по теории авиации, многие исследования по механике твердого тела, астрономии, математике, гидродинамике и гидравлике, прикладной механике, теории регулирования машин и механизмов и др. Участник создания Аэродинамического института в Кучино, под Москвой (1904), и др. Организатор и первый руководитель (с 1918) Центрального аэрогидродинамического института (ЦАГИ).
Ряд исследований Жуковского был посвящен теории движения тяжелого твердого тела вокруг неподвижной точки, причем эти исследования были замечательны примененным в них геометрическим методом. Много внимания Жуковский уделил проблеме устойчивости движения. Ей была посвящена его докторская диссертация «О прочности движения» (1879, издана в 1882), послужившая основой для исследования устойчивости аэропланов в воздухе. Несколько работ было посвящено теории гироскопов.
Н.Е.Жуковский (1847-1921)

В 1882 и 1886 в связи с выдвинутой тогда технической проблемой создания судов с реактивными движителями Жуковский дал методы расчета воздействия на сосуд втекающей в него и вытекающей из него жидкости. К работам по гидромеханике относится исследование по теории качки морских судов. Важным вопросам гидродинамики была посвящена магистерская диссертация Жуковского «Кинематика жидкого тела» (1876), в которой он предложил геометрическую теорию движения изменяемой системы. Некоторые результаты обширного исследования по гидромеханике «О движении твердого тела, имеющего полости, заполненные капельной жидкостью» (1885) были позднее использованы при решении космогонических проблем. В 1886 Жуковский создал свой курс «Лекции по гидродинамике», оказавший большое влияние на развитие этой области механики в России
Характерная для Жуковского практическая направленность научного творчества особенно отчетливо проявилась в его классических исследованиях по гидравлике. Этот цикл был связан с важнейшей технической проблемой водоснабжения крупных городов. Исследования Жуковского по фильтрации впоследствии были с большим успехом применены к вопросам механики добычи нефти. Теоретические и экспериментальные исследования сложного явления гидравлического удара позволили Жуковскому дать законченную теорию гидравлического тарана .

Строгая постановка задачи об устойчивости движения и указание наиболее общих методов ее решения, а также конкретное рассмотрение отдельных важнейших задач теории устойчивости принадлежат А. М. Ляпунову, и изложены им в фундаментальном сочинении “Общая задача об устойчивости движения” (1892). Им было дано определение устойчивого положения равновесия, которое выглядит следующим образом: если при данном r (радиус сферы) можно выбрать такое, сколь угодно малое, но не равное нулю значение h (начальная энергия), что во все последующее время частица не выйдет за пределы сферы радиуса r, то положение равновесия в данной точке называется устойчивым. Ляпунов связал решение задачи об устойчивости с рассмотрением некоторых функций, из сопоставления знаков которых со знаками их производных по времени можно заключить об устойчивости или неустойчивости рассматриваемого состояния движения (“вторая метода Ляпунова”). С помощью этого метода Ляпунов в своих теоремах об устойчивости по первому приближению указал границы применимости метода малых колебаний материальной системы около положения ее устойчивого равновесия (впервые изложенной в “Аналитической механике” Лагранжа).
Ляпунов А.М. (1857-1918)

Динамика в России XVII в.
Последующее развитие теории малых колебаний в XIX в. было связано, главным образом, с учетом влияния сопротивлений, приводящих к затуханию колебаний, и внешних возмущающих сил, создающих вынужденные колебания. Теория вынужденных колебаний и учение о резонансе появились в ответ на запросы машинной техники и, в первую очередь, в связи со строительством железнодорожных мостов и созданием быстроходных паровозов. Другой важной отраслью техники, развитие которой потребовало приложения методов теории колебаний, было регуляторостроение. Основоположником современной динамики процесса регулирования является русский ученый и инженер И. А. Вышнеградский.

И.А. Вышнеградский (1831-1895)
Вышнеградский Иван Алексеевич (1831-95), российский государственный деятель и предприниматель. В 1886-94 Почетный член Петербургской АН (1888). Из семьи священника. Математик, ученик М. В. Остроградского. Один из основоположников теории автоматического регулирования, основатель научной школы по конструированию машин. В 1865-75 профессор прикладной математики в Михайловской артиллерийской академии, в 1875-78 директор Петербургского технологического института. Одновременно с конца 1860-х гг. до 1878 служил инженером-механиком в Главном артиллерийском управлении, где по его разработкам был оборудован Охтинский пороховой завод, механические мастерские Петербургского арсенала.

В 1877 г. в работе “О регуляторах прямого действия” Вышнеградский впервые сформулировал известное неравенство, которому должна удовлетворять устойчиво работающая машина, снабженная регулятором.

СССР в начале XX века
Дальнейшее развитие теории малых колебаний было тесно связано с возникновением отдельных крупных технических проблем. В XX в. задачи электротехники, радиотехники, теории автоматического регулирования машин и производственных процессов, технической акустики и другие вызвали к жизни новую область науки – теорию нелинейных колебаний. Основы этой науки были заложены в трудах А. М. Ляпунова и французского математика А. Пуанкаре, а дальнейшее развитие в, результате которого образовалась новая, быстро растущая дисциплина, обязано достижениям советских ученых.

А.Н.Крылов (1863-1945)
Российский кораблестроитель, механик и математик, академик АН СССР (1925; академик Петербургской АН с 1916, академик РАН с 1917), Герой Социалистического Труда (1943). Участник проектирования и постройки первых русских линкоров. Труды по теории корабля, магнитных и гироскопических компасов, артиллерии, механике, математике, истории науки. Создал ряд корабельных и артиллерийских приборов. Государственная премия СССР (1941). вся деятельность Крылова была посвящена применению современных достижений математики и механики к решению важнейших технических задач

МЕЩЕРСКИЙ Иван Васильевич (1859-1935)
Российский ученый. Профессор Санкт-Петербургского политехнического института (с 1902). Труды по механике тел переменной массы, ставшие теоретической основой разработок многих проблем реактивной техники – Ему принадлежит основополагающая роль в создании новой области теоретической механики – динамики переменной массы. В 1897 г. им была опубликована фундаментальная работа “Динамика точки переменной массы”.

С.А.Чаплыгин (1869-1842)
Российский ученый, один из основоположников аэродинамики, академик АН СССР (1929), Герой Социалистического Труда (1941). Труды по теоретической механике, гидро-, аэро- и газовой динамике. Совместно с Н. Е. Жуковским участвовал в организации Центрального аэрогидродинамического института (ЦАГИ, 1918, в 1921-41 научный руководитель).
С. А. Чаплыгину принадлежит фундаментальное исследование в области газовой динамики, указавшее на многие десятки лет вперед пути развития аэродинамики больших скоростей

Открытия советских ученых
Существенных результатов достигли советские ученые в области теории упругости. Ими были проведены исследования по теории изгиба плит и общим решениям задач теории упругости, по плоской задаче теории упругости, по вариационным методам теории упругости, по строительной механике, по теории пластичности, по теории идеальной жидкости, по динамике сжимаемой жидкости и газовой динамике, по теории фильтрации движений, что способствовало быстрому развитию советской гидроаэродинамики, были развиты динамические задачи в теории упругости. Результаты первостепенной важности, полученные учеными Советского Союза по теории нелинейных колебаний, утвердили за СССР ведущую роль в этой области.

Н.Д.Папалекси (1880-1947)
Российский радиофизик, один из основателей школы радиофизиков и радиотехников, академик АН СССР (1939). Совместно с Л. И. Мандельштамом выполнил основополагающие исследования по нелинейным колебаниям, разработал метод параметрического возбуждения электрических колебаний, предложил радиоинтерференциальный метод. Государственная премия СССР (1942).
Основные работы в области радиофизики, радиотехники, теории нелинейных колебаний Разрабатывал ламповые приемники для оборонных целей. Работал над усовершенствованием радиотелефонной связи. Внес большой вклад в теорию нелинейных колебаний. Создал параметрические генераторы.

Л.И.Мандельштам (1879-1944)

Эпилог….
“Все изменения, случающиеся в природе, проходят так, что если что-либо прибавится к чему-либо, то столько же отнимется от чего-то другого. Так, сколько к какому-нибудь телу присоединится материи, столько же отнимется от другого; сколько часов я употребляю в сон, столько же отнимаю от бдения и т. д. Так как этот закон природы всеобщ, то он простирается даже и в правила движения, и тело, побуждающее своим толчком другое к движению столько же теряет своего движения, сколько сообщает другому, движимому им”. (М.В. Ломоносов)