Содержание
- 2. ФУНКЦІЯ – ЦЕ ОСНОВНЕ ПОНЯТТЯ МАТЕМАТИЧНОГО АНАЛІЗУ. ТЕРМІН “ФУНКЦІЯ” ВПЕРШЕ ЗАПРОПОНУВАВ ГОТФРІД ВІЛЬГЕЛЬМ ЛЕЙБНІЦ У ХVІІ
- 3. ВЕЛИКИЙ ВНЕСОК У РОЗВИТОК І РОЗШИРЕННЯ ПОНЯТТЯ “ФУНКЦІЯ” ЗРОБИЛИ ВИДАТНІ ВЧЕНІ Й.БЕРНУЛЛІ Л.ЕЙЛЕР М.І.ЛОБАЧЕВСЬКИЙ
- 4. ЗАЛЕЖНІСТЬ ЗМІННОЇ У ВІД ЗМІННОЇ Х НАЗИВАЮТЬ ФУНКЦІЄЮ, ЯКЩО КОЖНОМУ ЗНАЧЕННЮ Х ВІДПОВІДАЄ ЄДИНЕ ЗНАЧЕННЯ У.
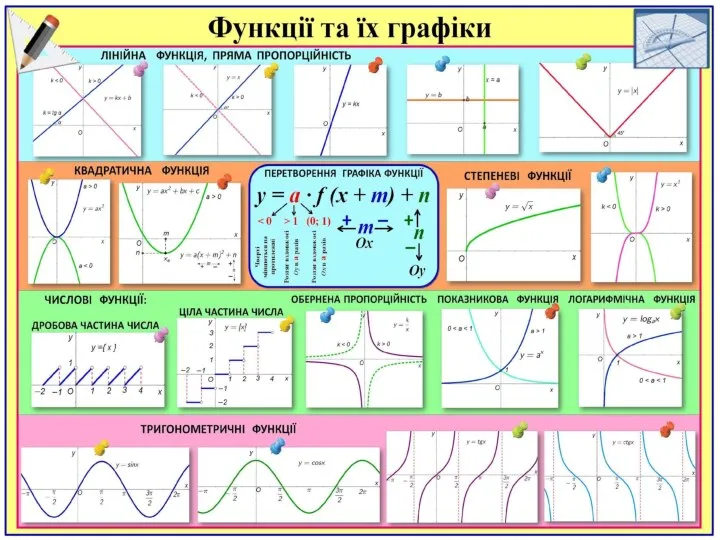
- 5. Способи задання функції
- 6. 1)“ЗАДАНО ТАКУ ЗАЛЕЖНІСТЬ ЗМІННОЇ У ВІД ЗМІННОЇ Х, ПРИ ЯКІЙ КОЖНОМУ ЗНАЧЕННЮ У ПОСТАВЛЕНО У ВІДПОВІДНІСТЬ
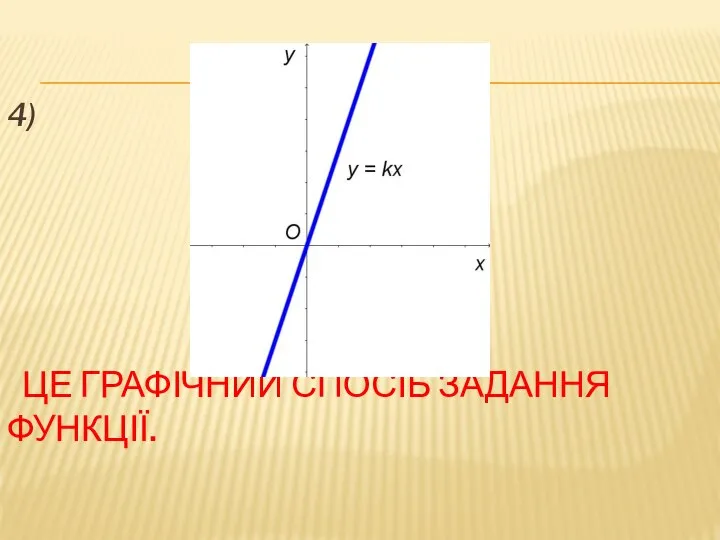
- 7. 4) ЦЕ ГРАФІЧНИЙ СПОСІБ ЗАДАННЯ ФУНКЦІЇ.
- 8. Область визначення функції
- 9. ОБЛАСТЬ ВИЗНАЧЕННЯ ФУНКЦІЇ – ЦЕ МНОЖИНА ЗНАЧЕНЬ, ЯКИХ МОЖЕ НАБУВАТИ АРГУМЕНТ Х ПОЗНАЧАЄТЬСЯ D(f)
- 10. ЗВЕРНІТЬ УВАГУ НА ОСОБЛИВІ ВИПАДКИ! 1) ІРРАЦІОНАЛЬНА ФУНКЦІЯ О.В. : f(x) ≥ 0 2) ДРОБОВО-РАЦІОНАЛЬНА ФУНКЦІЯ
- 11. Область значень функції
- 12. ОБЛАСТЬ ЗНАЧЕНЬ ФУНКЦІЇ – ЦЕ МНОЖИНА ЗНАЧЕНЬ ЗАЛЕЖНОЇ ЗМІННОЇ У, ЯКИХ ВОНА НАБУВАЄ ПРИ ВСІХ Х
- 13. ЗВЕРНІТЬ УВАГУ НА ОСОБЛИВІ ВИПАДКИ! 1) ІРРАЦІОНАЛЬНА ФУНКЦІЯ О.З. : у ≥ 0 2) ДРОБОВО-РАЦІОНАЛЬНА ФУНКЦІЯ
- 14. ЗВЕРНІТЬ УВАГУ НА ОСОБЛИВІ ВИПАДКИ! 4) МОДУЛЬ ФУНКЦІЇ О.З. : у ≥ 0
- 15. Графік функції
- 16. ГРАФІК ФУНКЦІЇ – ЦЕ МНОЖИНА УСІХ ТОЧОК З КООРДИНАТАМИ ( х; у ) КООРДИНАТНОЇ ПЛОЩИНИ, ЯКІ
- 18. Нулі функції
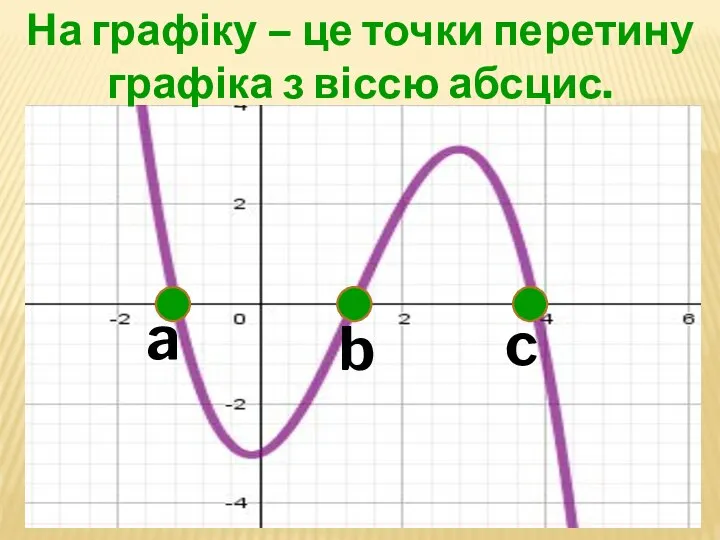
- 19. Нулі функції – це точки х, у яких значення функції дорівнює 0, тобто f(х) = 0.
- 20. На графіку – це точки перетину графіка з віссю абсцис. a b c
- 21. Парність та непарність функції
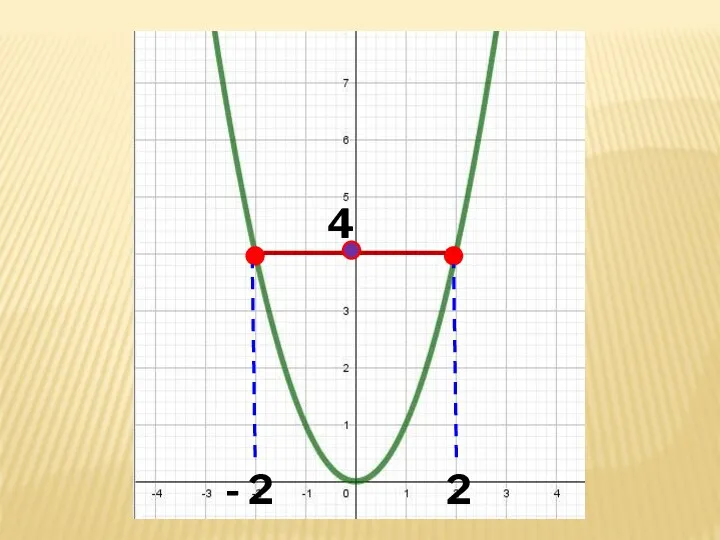
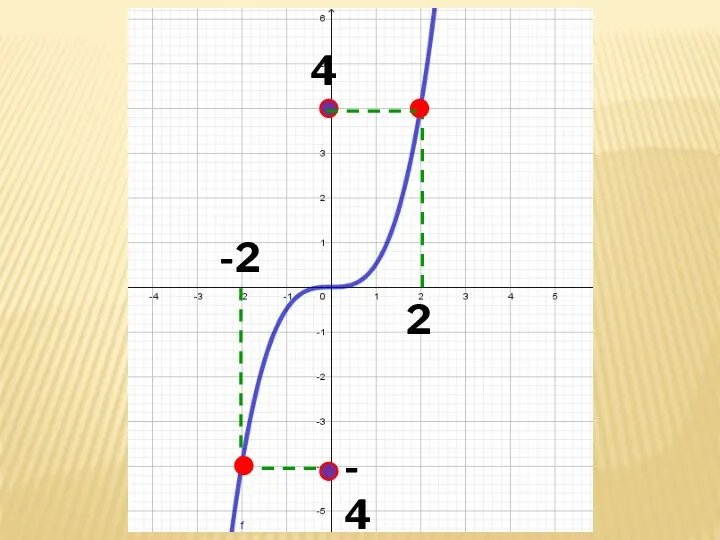
- 22. - 2 2 4
- 23. Протилежним аргументам х = 2 та х = - 2 відповідає однакове значення функції у =
- 24. 2 4 -2 - 4
- 25. Протилежним аргументам х = 2 та х = - 2 відповідають протилежні значення функції у =
- 26. ЯКЩО ДЛЯ АРГУМЕНТІВ х = а ТА х = - а ЗНАЧЕННЯ ФУНКЦІЇ f(a) = f(
- 27. ЯКЩО ДЛЯ АРГУМЕНТІВ х = а ТА х = - а ЗНАЧЕННЯ ФУНКЦІЇ f(a) = -
- 28. Зростання та спадання функції
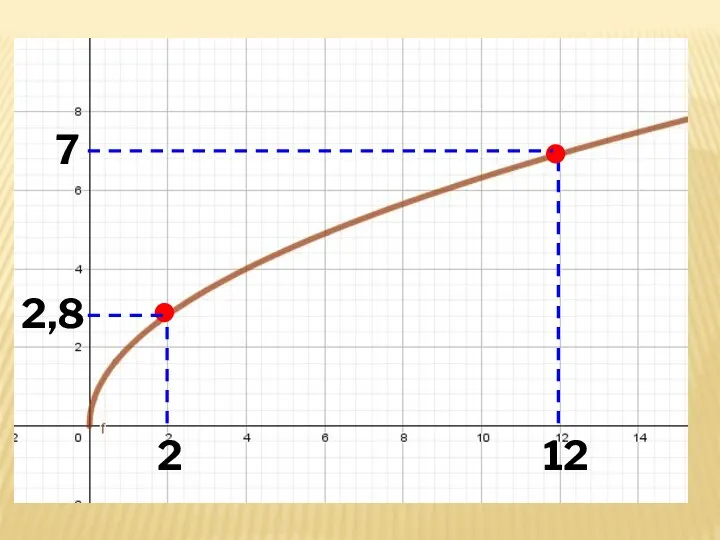
- 29. 2 2,8 12 7
- 30. ЗНАЧЕННЮ АРГУМЕНТА х = 2 ВІДПОВІДАЄ ЗНАЧЕННЯ ФУНКЦІЇ У = 2,8. Тобто, більшому значенню аргумента відповідає
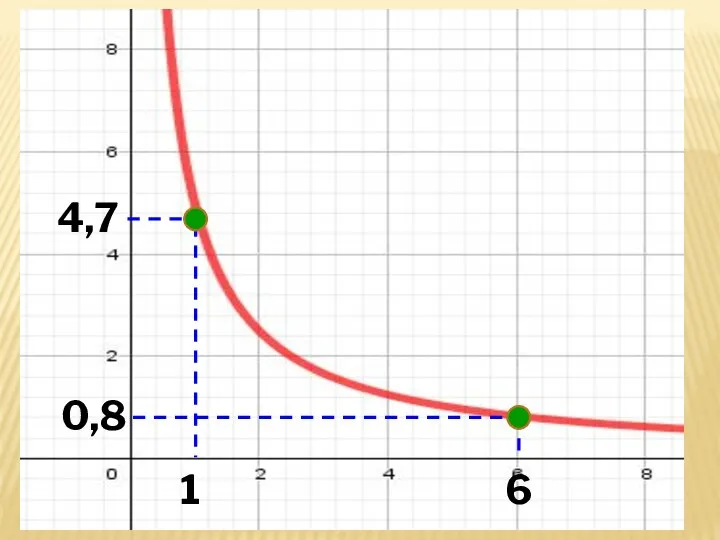
- 31. 1 4,7 6 0,8
- 32. ЗНАЧЕННЮ АРГУМЕНТА х = 1 ВІДПОВІДАЄ ЗНАЧЕННЯ ФУНКЦІЇ У = 4,7. Тобто, більшому значенню аргумента відповідає
- 33. ЯКЩО ДЛЯ АРГУМЕНТІВ х = а ТА х = b ТАКИХ, ЩО a Теорема 3.
- 34. ЯКЩО ДЛЯ АРГУМЕНТІВ х = а ТА х = b ТАКИХ, ЩО a f(b), ТО ТАКА
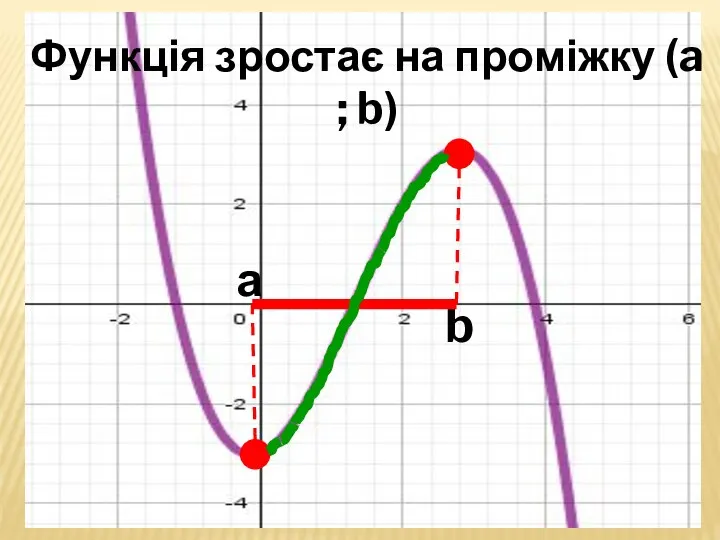
- 35. а b Функція зростає на проміжку (a ; b)
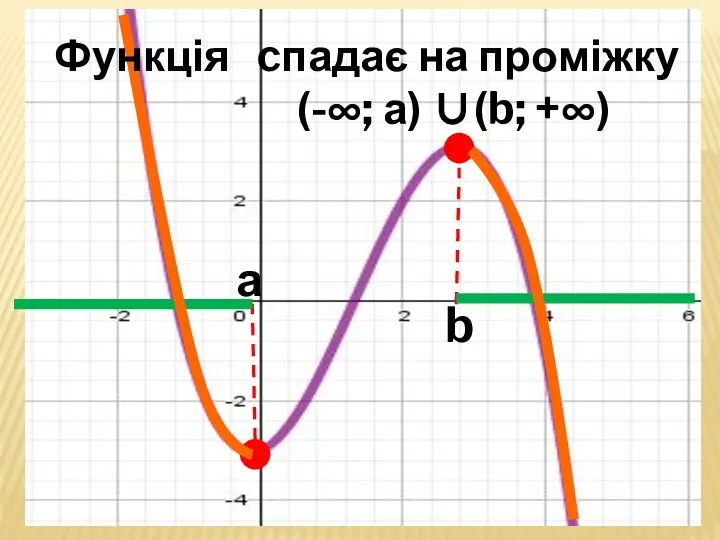
- 36. а b Функція cпадає на проміжку (-∞; а) ∪(b; +∞)
- 37. Знакосталість функції
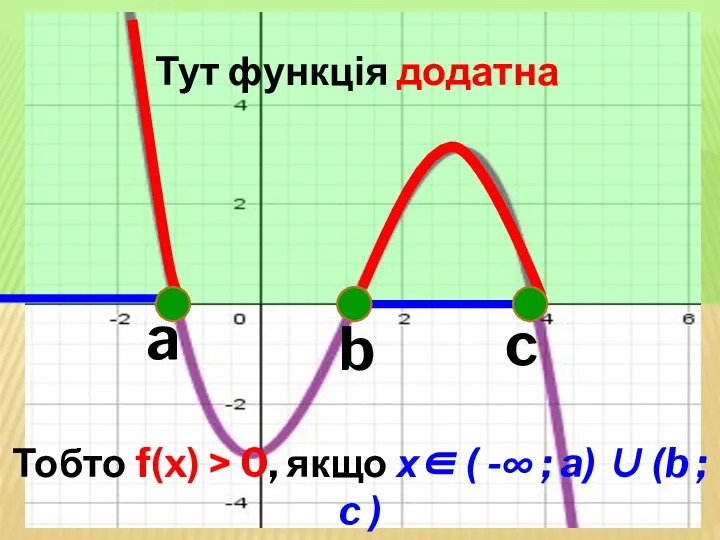
- 38. Тут функція додатна Тобто f(x) > 0, якщо х∈ ( -∞ ; a) ∪ (b ;
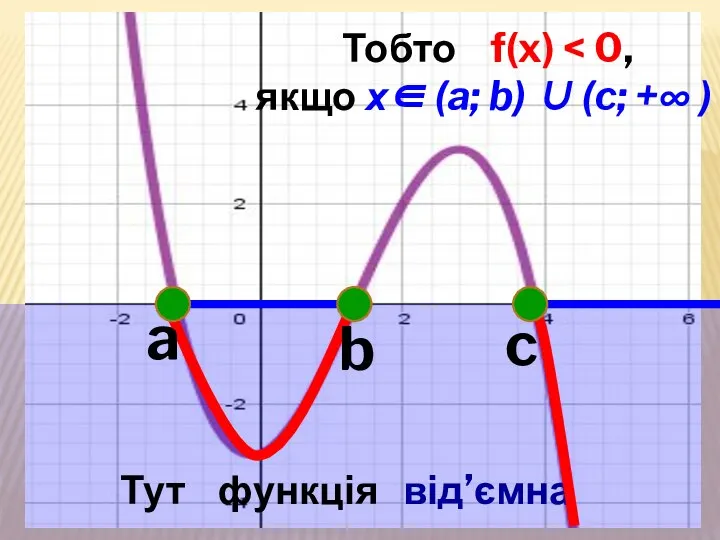
- 39. Тут функція від’ємна a b c Тобто f(x) якщо х∈ (a; b) ∪ (c; +∞ )
- 41. Скачать презентацию



























 Ведущие пояски артиллерийских снарядов
Ведущие пояски артиллерийских снарядов Некоторые проблемы внедрения Ajax технологии в ASP.NET проекты Методы их решения
Некоторые проблемы внедрения Ajax технологии в ASP.NET проекты Методы их решения Тема:»Вредные привычки »
Тема:»Вредные привычки » Преображение Господне
Преображение Господне АРКСИНУС, АРККОСИНУС, АРКТАНГЕНС, АРККОТАНГЕНС.
АРКСИНУС, АРККОСИНУС, АРКТАНГЕНС, АРККОТАНГЕНС. Портрет в искусстве России
Портрет в искусстве России Физическая культура личности и её взаимосвязь с общей культурой общества
Физическая культура личности и её взаимосвязь с общей культурой общества Недвижимость. Торги, лот №6, г. Хабаровск
Недвижимость. Торги, лот №6, г. Хабаровск Первый искусственный спутник Земли
Первый искусственный спутник Земли The biggest cities of Great Britain
The biggest cities of Great Britain Защита населения и территорий в условиях землетрясений
Защита населения и территорий в условиях землетрясений Гео-шоу. Команда Эксперты. Должность товароведа
Гео-шоу. Команда Эксперты. Должность товароведа Система контроля и сигнализации опасных накоплений. Оборудование и комплектные устройства
Система контроля и сигнализации опасных накоплений. Оборудование и комплектные устройства Буду помнить!
Буду помнить! Полет Ю.А. Гагарина в космос
Полет Ю.А. Гагарина в космос Современные проблемы непостоянства кадров в организации
Современные проблемы непостоянства кадров в организации 1С:Документооборот для автоматизации государственных учреждений, МЭДО и СМЭВ
1С:Документооборот для автоматизации государственных учреждений, МЭДО и СМЭВ Практическая работа по географии
Практическая работа по географии Апельсиновый нектар
Апельсиновый нектар Право и организация социального обеспечения
Право и организация социального обеспечения МатематикА
МатематикА «НАША НОВАЯ ШКОЛА» Послание Президента РФ Д.А.Медведева Федеральному собранию Российской Федерации 5 ноября 2008г.
«НАША НОВАЯ ШКОЛА» Послание Президента РФ Д.А.Медведева Федеральному собранию Российской Федерации 5 ноября 2008г. Ислам
Ислам Социология массовых коммуникаций
Социология массовых коммуникаций Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов 7 класс
Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов 7 класс  Встреча весны
Встреча весны Конкурс презентаций «Скажи здоровью – Да» СКАЖИ ЗДОРОВОМУ ОБРАЗУ ЖИЗНИ – ДА, А ВРЕДНЫМ ПРИВЫЧКАМ – НЕТ!!! Выполнил: Федоров Д.А., уч
Конкурс презентаций «Скажи здоровью – Да» СКАЖИ ЗДОРОВОМУ ОБРАЗУ ЖИЗНИ – ДА, А ВРЕДНЫМ ПРИВЫЧКАМ – НЕТ!!! Выполнил: Федоров Д.А., уч Итоги работы группы управленцев
Итоги работы группы управленцев