Г.Е.Цейтлин, Л.М.Захария

Алгебраизация знаний – обзор подходов
Данный доклад посвящен рассмотрению проблематики полноты (аксиоматической и функциональной) в аспекте предпринятых на Западе усилий по алгебраизации современного программирования
Ноден П., Китте К. Алгебраическая алгоритмика. М.:Мир, 1999 г 720 с.
Чарнецки К., Айзенекер У. Порождающее программирование: методы, инструменты, применение. Для профессионалов.- СПб.: Питер,2005. - 731 с.
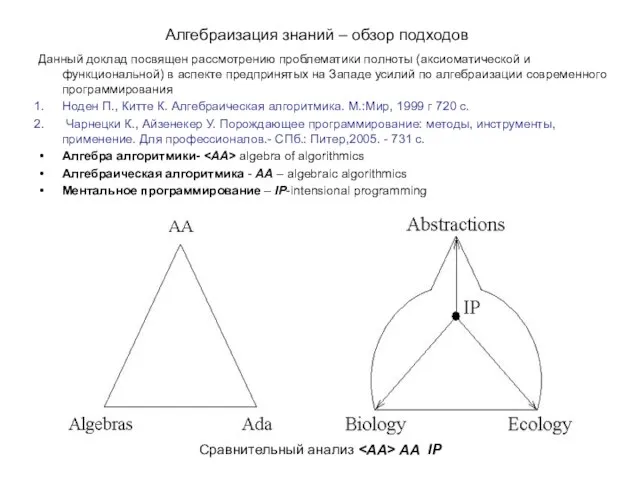
Алгебра алгоритмики- <АА> algebra of algorithmics
Алгебраическая алгоритмика - АА – algebraic algorithmics
Ментальное программирование – IP-intensional programming
Сравнительный анализ <АА> АА IP

Три аспекта представления знаний в алгебре алгоритмики
2.1 Абстракции – три формы представления алгоритмов
Аналитическая (регулярная схема)
Текстовая (САА схема)
Визуальная – граф-схемная
2.2. Биология – теория клонов
Клон – семейство алгебр с функционально полными сигнатурами операций. Каждая алгебра – прикладной язык описания алгоритмов в актуальной ПРО для непрограммирующих пользователей
Определение:
Под клоном понимают одноосновную (или многоосновную) универсальную алгебру вида:
К =
,
де A - основа, являющаяся множеством однотипных функций; (А – представительная алгебра по Успенскому).
SUPER -сигнатура, состоящая из операции суперпозиции функций и операций отождествления и переименования переменных
2.3. Экология – инструментальные средства синтеза программ

Общность и специфика проблемы полноты в развитии алгебры алгоритмики
3.1. Аксиоматическая полнота:
Теорема Геделя о неполноте формальной арифметики
Теорема Геделя о полноте узкого исчисления предикатов
3.2. Функциональная полнота
Теорема Поста о функциональной полноте 2-значной алгебры логики
Функциональная полнота базируется на критерии полноты выбранной сигнатуры операций представительной алгебры..
И функциональная, и аксиоматическая полнота предусматривают сводимость абстракций к каноническим формам посредством применения системы тождеств или законов представительных алгебр.

Классификация_клонов.
В рамках алгоритмики исследованы следующие пары:
представительная алгебра --- связанный с ней алгоритмический клон.
Каждой паре соответствует определенный метод или технология программирования:
1. Структурное программирование: алгебра Дейкстры (АД) - клон Дейкстры (КД);
Системы алгоритмических алгебр САА Глушкова - клон Глушкова (КГ);
2. Неструктурное программирование : алгебра Янова (АЯ) - клон Янова (КЯ);
3. Визуальное программирование алгебра граф-схем Калужнина (АК) - клон Калужнина(КлК)
Каждая представительная алгебра является двухосновной. Логическая основа состоит из булевых операций и операции прогнозирования в случае САА .
Алгоритмические клоны в качестве логической компоненты содержат клон Поста.
Для алгебры Клини (алгебры регулярных событий) построен клон Клини.
Теорема об изоморфизме
Алгебра Клини изоморфна алгебре Кодда.
Следствие
Построение клона Кодда и доказательство для него теоремы о функциональной полноте

Кванторизация в алгебрах и ее связь с прогнозированием
Для расширения изобразительных средств представительной алгебры предложено ввести кванторы всеобщности и существования
Квантор всеобщности является теоретико-множественным пределом конъюнкции.
По правилу де Моргана отрицание квантора всеобщности определяет квантор существования
Кванторы предполагают наличие памяти. Наличие памяти предполагает и операция прогнозирования алгебры Глушкова.
Кванторы существенно используются в реляционных алгебрах, при исследовании онтологий

Алгебра алгоритмики – сфера приложений
Теория клонов –механизм исследования и формализации алгоритмических знаний предметных областей. Клон n-отношений
Инструментальные средства генерации программ
Алгеброалгоритмические базы знаний исследованных ПО
Экономические приложения: учетные модели, базы запросов в многомерным БД
Web-приложения
Гипертектовый редактор текстов, формул, рисунков на основе редактора Lateh

САА – как средство формализации алгоритмических знаний ПО – анализ ранее полученных основных результатов
Аналитическая форма представления алгоритмов в виде САА схем (формульная, текстовая)
Мета-правила преобразования САА-схем как инструмент порождения новых алгоритмических знаний
свертка (укрупнение), развертка (детализация), переинтерпретация (свертка-равертка), трансформация схем алгоритмов.
Исследованы предметные области –сортировка и поиск
установлена алгоритмическая связь между ними: алгоритмы поиска получены в результате переинтепретации алгоритмов сортировки
Механизм розметки как механизм связи между символьными последовательностями данных - операторами и предикатами САА схем
Механизм передачи параметров в текстовых идентификаторах
Модульная структура реализаций елементарных (конечных) операторов и условий
Инструментарий состоит из ДСП конструктора, синтезатора програмных продуктов, интепретатора САА-схем

Клон Кодда n-відношень
Клон n-отношений формализирует проектирование алгоритмичних знаний в предметных областях с большими структурированными обьемами данных и отображает метод проектирования от данных.
n-арное отношение - произвольное подмножество декартового произведения М1 x М2 x...x Мn.
Отношение R – функционально, если с ним связана функция f так, что для любых (а1,…,аn), принадлежащих отношению, аn=f(а1,…,аn-1). Введение понятия функциональности отношений связывает данные с алгоритмами их обработки.
Свертка де Моргана формализует процесс связывания двух таблиць баз данных по значению поля и формализует композицию n-отношений.
І-суперпозиция – обобщение сверки а де Моргана
Операции алгебры Кодда
Обьединение -- выборка (вибор строк)
Песечение -- проекция (вибор столбцов)
Разность -- светка де Моргана
Декартовое произведение -- деление
І-суперпозиция – сумарный запрос в SQL., ее операции являются суперпозициями операций алгебры Кодда, например перекрестный запрос – і-суперпозиція(группирование по значениям столбцов (группирование по значениях строк)
Задачи – проблема функциональной полноты, канонические формы, трансформация выражений в алгебре n-отношений

Инструментальные средства алгебры алгоритмики
Компоненты инструментария
Построение схем-алгоритмов: ДСП конструктор, робота з аналитической формой представления алгоритма, редактор граф-схем
Алгоритм – иерархическая структура взаимосвязанных схем составных обьектов – аспект читабельности, понятие гипертекста
Пстроение аналитической формулы, мета правила конструирования, інтепретація, трансформация
Наполнение базы интепретаций элементарных обьектов схем, гиперсхема проекта, клас як АТД, инкапсуляция АТД, реализация механизма наследовани, механизм передачи параметров в элементарных обьектах, базовый язык – Java
Інструментарий для роботи з базами данных:
Визуальные средства создания и манипуляции (операции алгебры n-отношений) таблицы, создание за шаблоном шаблоном,
визуальные средства построения запросов и их отображение в виде SQL выражений и виражений в алгебре n-отношений
работа с ведомостями, стандартные операции над ними, задание функций обработки строк таблиц (Excel)