Содержание
- 2. Выполнил: Цун Иосиф Менделевич, профессор кафедры алгебры и геометрии МаГУ, кандидат технических наук E-mail: [email protected] http://im-ts.narod.ru
- 3. Основное построение № 1 Отложить на данном луче от его начала отрезок, равный данному отрезку a.
- 4. Основное построение № 2 Отложить от данного луча в данную полуплоскость угол, равный данному углу. Построение:
- 5. Основное построение № 3 Построить треугольник по трём сторонам. На произвольной прямой откладываем отрезок АВ =
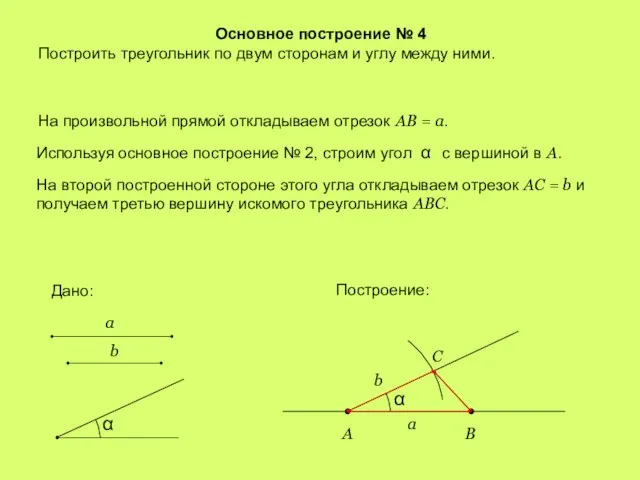
- 6. Основное построение № 4 Построить треугольник по двум сторонам и углу между ними. На произвольной прямой
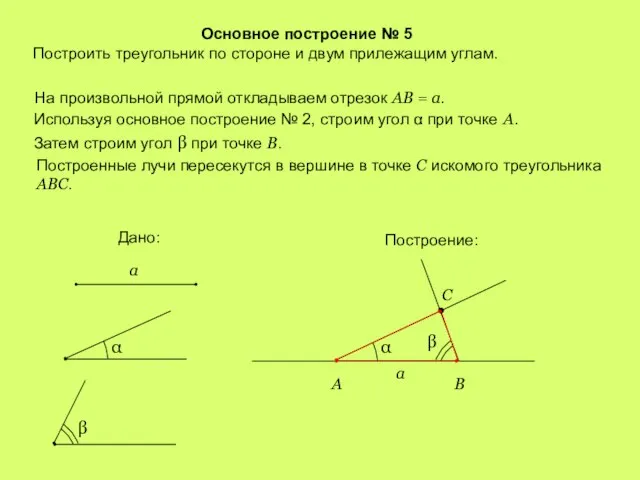
- 7. Основное построение № 5 Построить треугольник по стороне и двум прилежащим углам. На произвольной прямой откладываем
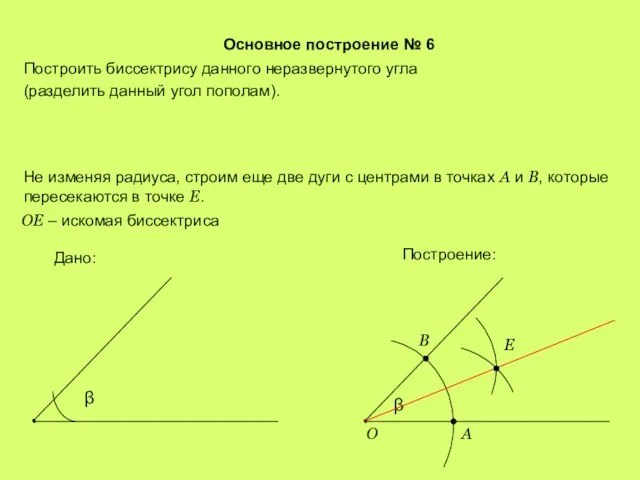
- 8. Основное построение № 6 Построить биссектрису данного неразвернутого угла (разделить данный угол пополам). Построение: β B
- 9. Основное построение № 7 Построить серединный перпендикуляр данного отрезка (аналогично выполняется построение середины данного отрезка). С
- 10. Основное построение № 8 Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Случай
- 11. Основное построение № 8 Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Случай
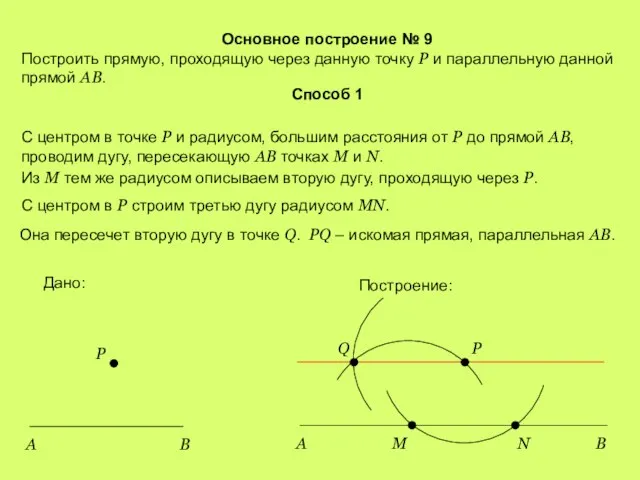
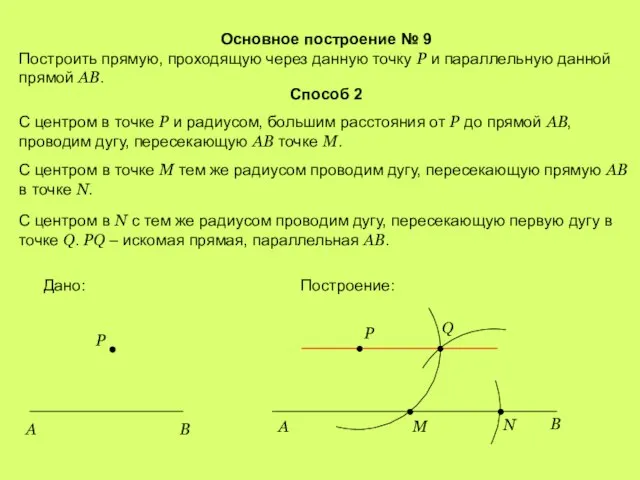
- 12. Основное построение № 9 Построить прямую, проходящую через данную точку Р и параллельную данной прямой АВ.
- 13. Основное построение № 9 Построить прямую, проходящую через данную точку Р и параллельную данной прямой АВ.
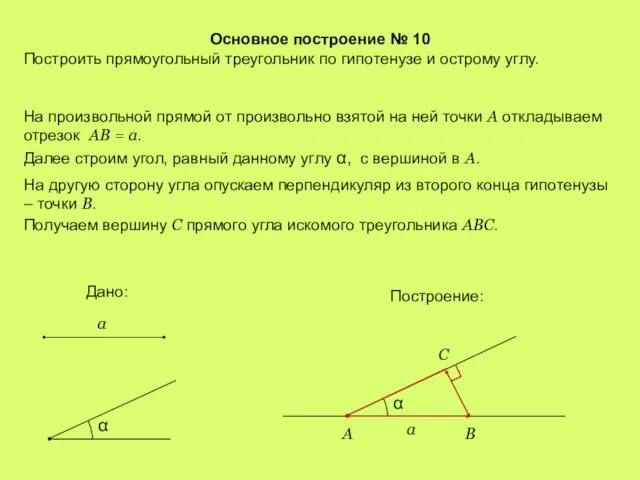
- 14. Основное построение № 10 Построить прямоугольный треугольник по гипотенузе и острому углу. На произвольной прямой от
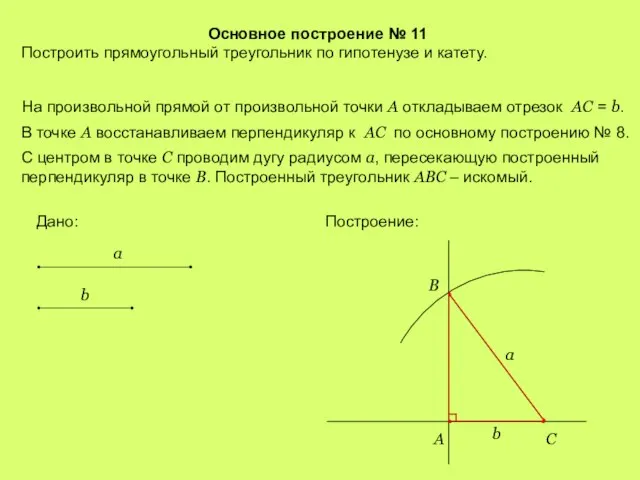
- 15. Основное построение № 11 Построить прямоугольный треугольник по гипотенузе и катету. На произвольной прямой от произвольной
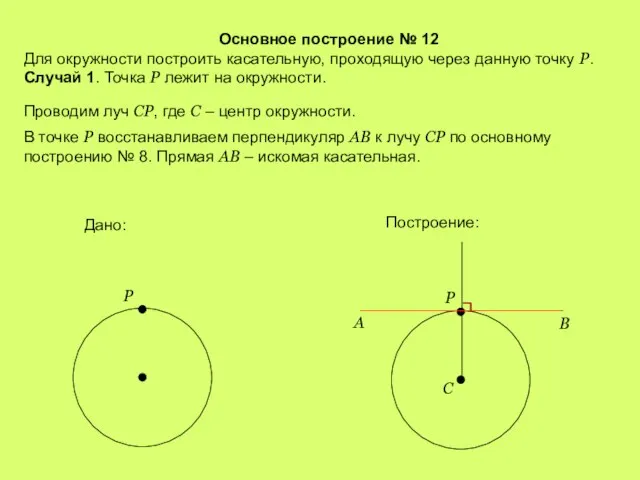
- 16. Основное построение № 12 Для окружности построить касательную, проходящую через данную точку Р. Случай 1. Точка
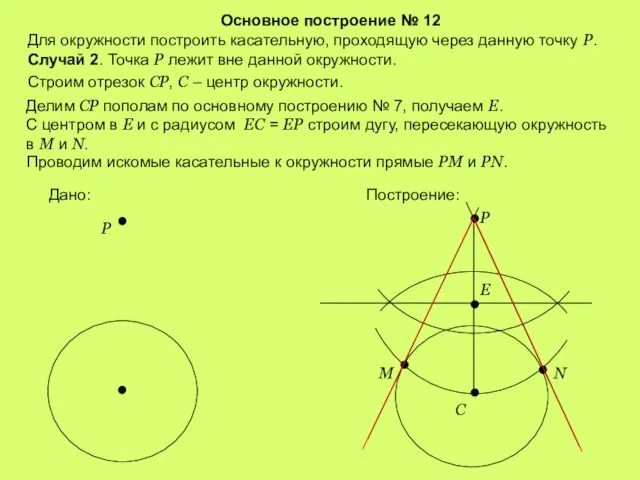
- 17. Основное построение № 12 Для окружности построить касательную, проходящую через данную точку Р. Случай 2. Точка
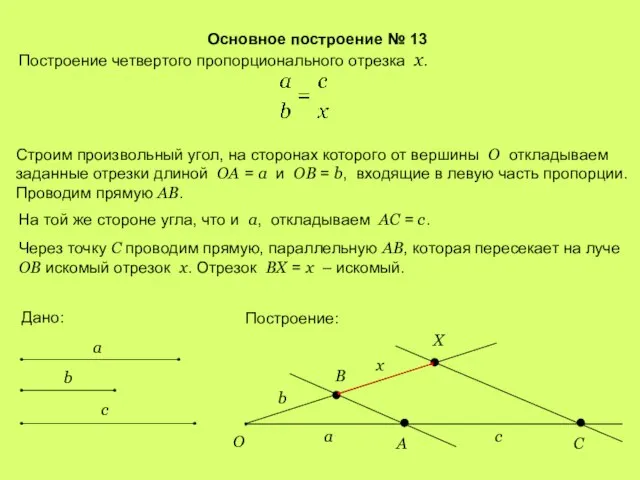
- 18. Основное построение № 13 Построение четвертого пропорционального отрезка x. Строим произвольный угол, на сторонах которого от
- 20. Скачать презентацию







 Электронная Земля:сетевая среда поиска,интеграции и анализа геоданных
Электронная Земля:сетевая среда поиска,интеграции и анализа геоданных Финансовое прогнозирование в образовательном учреждении
Финансовое прогнозирование в образовательном учреждении Японский дубляж немых фильмов
Японский дубляж немых фильмов Сюжет и содержание в картине. 7 класс
Сюжет и содержание в картине. 7 класс Управление и мониторинг ИТ-инфраструктуры
Управление и мониторинг ИТ-инфраструктуры Правила перспективы Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №6 г.Зарайска Московской
Правила перспективы Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №6 г.Зарайска Московской  Российский потенциал импортозамещающих полимерных пленок
Российский потенциал импортозамещающих полимерных пленок Страна ЗДОРОВЬЯ
Страна ЗДОРОВЬЯ Сила воли. Мотивация. Цель
Сила воли. Мотивация. Цель Административное право
Административное право Политическая система и политический режим
Политическая система и политический режим Наблюдения за семьёй серых ворон в гнездовой период
Наблюдения за семьёй серых ворон в гнездовой период Почему об одном я пою И всегда об одном говорю – Об Иисусе Христе дорогом. Искупителе дивном моем?
Почему об одном я пою И всегда об одном говорю – Об Иисусе Христе дорогом. Искупителе дивном моем? Тариф по индивидуальной банковской ячейке
Тариф по индивидуальной банковской ячейке Взаимосвязь цветовых предпочтений и типа темперамента человека
Взаимосвязь цветовых предпочтений и типа темперамента человека Революционная технология увеличения ресниц MD Lash Factor Врач дерматокосметолог, физиотерапевт Ю.С. Ляшенко Санкт-Петербург, апрель 20
Революционная технология увеличения ресниц MD Lash Factor Врач дерматокосметолог, физиотерапевт Ю.С. Ляшенко Санкт-Петербург, апрель 20 Компьютерная графика
Компьютерная графика Решение простейших логарифмических неравенств
Решение простейших логарифмических неравенств Стоимость на месяц
Стоимость на месяц ФУТБОЛИСТЫ ЗЕНИТА
ФУТБОЛИСТЫ ЗЕНИТА Культурная среда международного бизнеса
Культурная среда международного бизнеса 4-ядерный процессор Intel® Xeon® 7300
4-ядерный процессор Intel® Xeon® 7300 Мотив заката на пейзаже
Мотив заката на пейзаже Природоохранное законодательство штата Аляска:Требования для предприятий отрасли по разливам
Природоохранное законодательство штата Аляска:Требования для предприятий отрасли по разливам Other forms of tax supervision
Other forms of tax supervision  Особенности использования TimesTen In-Memory Database в высоконагруженной среде
Особенности использования TimesTen In-Memory Database в высоконагруженной среде Презентация на тему: Конфликты. Способы выхода из конфликта. Способы предупреждения конфликтной ситуации
Презентация на тему: Конфликты. Способы выхода из конфликта. Способы предупреждения конфликтной ситуации Иммунитет при туберкулезе
Иммунитет при туберкулезе